NYOJ：题目860 又见01背包

题目链接：http://acm.nyist.net/JudgeOnline/problem.php?pid=860

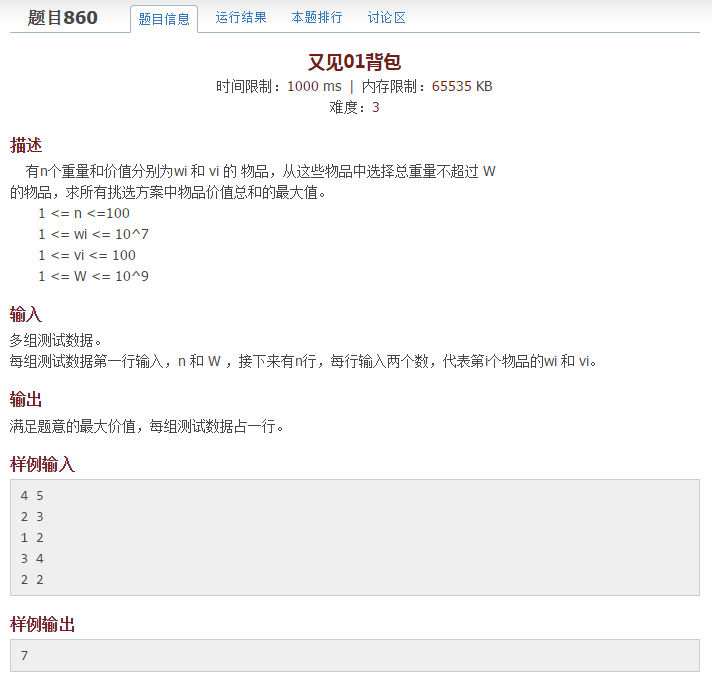
方法一：不用滚动数组（方法二为用滚动数组，为方法一的简化）

动态规划分析:最少要拿总价值一定，求所拿的最小质量(根据"最大能拿总重量一定，求能拿的最大价值"原理推导)

(PS:为了更好的理解，先不用滚动数组，直接开了两个数组，第一个数组用来储存最少要拿总价值为j时所拿的最小质量，第二个数组用来储存第一个的改变前状态)
例:
最大总质量sw = 5,物品数量n = 4;
          1   2  3  4 <-第i个物品
w[] = {2, 1, 3, 2} //重量
v[] = {3, 2, 4, 2} //价值
最大总质量sw = 5,最大总价值sv = 11,物品数量n = 4;

分析打表结果如下：

 #include<iostream>
 using namespace std;
 int main() {
   int n, sw, sv, v[], w[], m[], b[];  //n为物品数量,sw为总重量,sv为总价值
   while(cin >> n >> sw) {      //m[j]为最少要拿总价值为j时所拿的最小质量
     sv = ;                    //b[i]用来储存m[i]的上一个状态,如果用滚动数组方法就可以去掉b[]数组
     for(int i = ; i <= n; i++) {
       cin >> w[i] >> v[i];
       sv += v[i];
     }
     for(int j = ; j <= ; j++) {
       m[j] = ;  //初始化为题目范围内最大值
       b[j] = m[j];
     }
     m[] = b[] = ;
     for(int i = ; i <= n; i++) {
       for(int j = ; j <= sv; j++) {
         if(j >= v[i]) m[j] = min(b[j], b[j-v[i]]+w[i]);
         else m[j] = min(b[j], w[i]);
       }
       for(int j = ; j <= sv; j++) {
         b[j] = m[j];
         //b[j] > 1000000000 ? cout << "+ " : cout << b[j] << " ";    //去掉这两行注释可打表结果
       }
       //cout << endl;
     }
     int big = ;  //从价值为1开始找所有能拿到的价值
     while(big <= sv && b[big] <= sw) big++;
     cout << big- << endl;
   }
 }

代码实现(点击展开)

方法二：用滚动数组（方法一的简化）

原理：利用方法一的表格，按照价值j倒序计算表中的值

 #include<iostream>
 using namespace std;
 int main() {
   int n, sw, sv, v[], w[], m[];  //n为物品数量,sw为总重量,sv为总价值
   while(cin >> n >> sw) {      //m[j]为最少要拿总价值为j时所拿的最小质量
     sv = ;
     for(int i = ; i <= n; i++) { cin >> w[i] >> v[i]; sv += v[i]; }
     for(int j = ; j <= ; j++) m[j] = ;  //初始化为题目范围内最大值
     for(int i = ; i <= n; i++) {
       for(int j = sv; j >= ; j--) {
         if(j >= v[i]) m[j] = min(m[j], m[j-v[i]]+w[i]);
         else m[j] = min(m[j], w[i]);
         //m[j] > 1000000000 ? cout << "+ " : cout << m[j] << " ";  //去掉这两行注释可打表结果
       }
       //cout << endl;
     }
     int big = ;  //从价值为1开始找所有能拿到的价值
     while(big <= sv && m[big] <= sw) big++;
     cout << big- << endl;
   }
 }

代码实现(点击展开)

开始写于：2016.5.20  ----志银