Expectation maximization - EM算法学习总结

原创博客，转载请注明出处 Leavingseason http://www.cnblogs.com/sylvanas2012/p/5053798.html

EM框架是一种求解最大似然概率估计的方法。往往用在存在隐藏变量的问题上。我这里特意用"框架"来称呼它，是因为EM算法不像一些常见的机器学习算法例如logistic regression， decision tree，只要把数据的输入输出格式固定了，直接调用工具包就可以使用。可以概括为一个两步骤的框架：

E-step：估计隐藏变量的概率分布期望函数（往往称之为Q函数，它的定义在下面会详细给出）；

M-step：求出使得Q函数最大的一组参数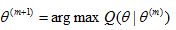

实际使用过程中，我们先要根据不同的问题先推导出Q函数，再套用E-M两步骤的框架。

下面来具体介绍为什么要引入EM算法？

不妨把问题的全部变量集（complete data）标记为X，可观测的变量集为Y，隐藏变量集为Z，其中X = (Y , Z) . 例如下图的HMM例子, S是隐变量，Y是观测值：

又例如，在GMM模型中（下文有实例） ，Y是所有观测到的点，z_i 表示 y_i 来自哪一个高斯分量，这是未知的。

问题要求解的是一组参数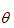， 使得最大。在求最大似然时，往往求的是对数最大：  （1）

对上式中的隐变量做积分（求和）：

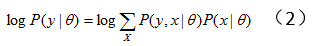
（2）式往往很难直接求解。于是产生了EM方法，此时我们想要最大化全变量（complete data）X的对数似然概率：假设我们已经有了一个模型参数的估计（第0时刻可以随机取一份初始值），基于这组模型参数我们可以求出一个此时刻X的概率分布函数。有了X的概率分布函数就可以写出的期望函数，然后解出使得期望函数最大的值，作为更新的参数。基于这个更新的再重复计算X的概率分布，以此迭代。流程如下：

Step 1： 随机选取初始值

Step 2：给定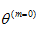和观测变量Y， 计算条件概率分布

Step 3：在step4中我们想要最大化，但是我们并不完全知道X（因为有一些隐变量），所以我们只好最大化的期望值， 而X的概率分布也在step 2 中计算出来了。所以现在要做的就是求期望，也称为Q函数：

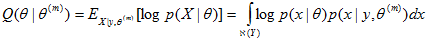
其中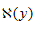，表示给定观测值y时所有可能的x取值范围，即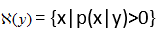

Step 4 求解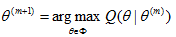

Step 5 回到step 2， 重复迭代下去。

为什么要通过引入Q函数来更新theta的值呢？因为它和我们的最大化终极目标（公式（1））有很微妙的关系：

定理1：

证明：在step4中，既然求解的是arg max， 那么必然有 。于是：

其中，（3）到（4）是因为X=(Y , Z), y=T(x), T是某种确定函数，所以当x确定了，y也就确定了（但反之不成立）；即：  而（4）中的log里面项因为不包含被积分变量x，所以可以直接提到积分外面。

所以E-M算法的每一次迭代，都不会使目标值变得更差。但是EM的结果并不能保证是全局最优的，有可能收敛到局部最优解。所以实际使用中还需要多取几种初始值试验。

实例：高斯混合模型GMM

假设从一个包含k个分量的高斯混合模型中随机独立采样了n个点 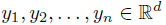， 现在要估计所有高斯分量的参数。 例如图（a）就是一个k=3的一维GMM。

高斯分布函数为：

令为第m次迭代时，第i个点来自第j个高斯分量的概率，那么：

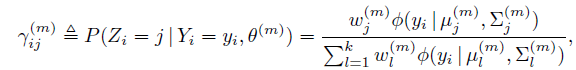     并且 

因为每个点是独立的，不难证明有：

于是首先写出每个：

忽略常数项，求和，完成E-step：

为简化表达，再令，

Q函数变为：

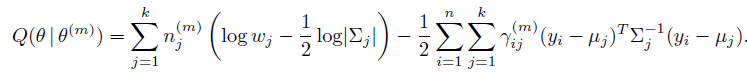
现在到了M-step了，我们要解出使得Q函数最大化的参数。最简单地做法是求导数为0的值。

首先求w。 因为w有一个约束：

可以使用拉格朗日乘子方法。 除去和w无关的项，写出新的目标函数：

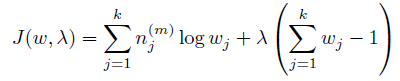
求导：

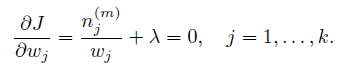
很容易解出w：

同理解出其他参数：

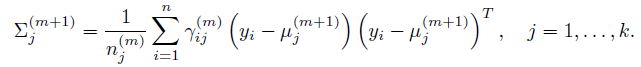
总结：个人觉得，EM算法里面最难懂的是Q函数。初次看教程的时候，很能迷惑人，要弄清楚是变量，是需要求解的；是已知量，是从上一轮迭代推导出的值。