Codeforces 556D Restructuring Company

传送门

Even the most successful company can go through a crisis period when you have to make a hard decision — to restructure, discard and merge departments, fire employees and do other unpleasant stuff. Let's consider the following model of a company.

There are n people working for the Large Software Company. Each person belongs to some department. Initially, each person works on his own project in his own department (thus, each company initially consists ofn departments, one person in each).

However, harsh times have come to the company and the management had to hire a crisis manager who would rebuild the working process in order to boost efficiency. Let's use team(person) to represent a team where person person works. A crisis manager can make decisions of two types:

1. Merge departments team(x) and team(y) into one large department containing all the employees ofteam(x) and team(y), where x and y (1 ≤ x, y ≤ n) — are numbers of two of some company employees. If team(x) matches team(y), then nothing happens.
2. Merge departments team(x), team(x + 1), ..., team(y), where x and y (1 ≤ x ≤ y ≤ n) — the numbers of some two employees of the company.

At that the crisis manager can sometimes wonder whether employees x and y (1 ≤ x, y ≤ n) work at the same department.

Help the crisis manager and answer all of his queries.

Input

The first line of the input contains two integers n and q (1 ≤ n ≤ 200 000, 1 ≤ q ≤ 500 000) — the number of the employees of the company and the number of queries the crisis manager has.

Next q lines contain the queries of the crisis manager. Each query looks like type x y, where . If type = 1 or type = 2, then the query represents the decision of a crisis manager about merging departments of the first and second types respectively. If type = 3, then your task is to determine whether employees x and y work at the same department. Note that x can be equal to y in the query of any type.

Output

For each question of type 3 print "YES" or "NO" (without the quotes), depending on whether the corresponding people work in the same department.

Sample test(s)

input

8 6
3 2 5
1 2 5
3 2 5
2 4 7
2 1 2
3 1 7

output

NO
YES
YES

---

这是一道很好的数据结构问题（我的看法）。

题意是:
$n$ 个元素编号为 $1$ 到 $n$，初始时这 $n$ 个元素各自处在一个（单元素）集合（singleton）中，要求支持下述三种操作
1 $x$, $y$ 将元素 $x$，$y$ 所在集合合并
2 $x$, $y$（$y\ge x$）将元素 $x, x+1, \dots, y$ 所在集合合并
3 $x$, $y$ 查询 $x$、$y$ 是否在同一集合内

---

Solution

并查集的即视感。

BTW：并查集的英文是 Disjoint Set 或者 Union-Find 或者 Merge-Find Set，Codeforces 的题解里将并查集称作 DSU（Disjoint Set Union）。

但这道题的操作 2 是裸并查集不能胜任的。第一发 T

后来想到操作 2 无需逐个合并，可采用二分合并这样可把合并次数降到 $\log(N)$。仍然 T。

看 Tutorial

This problem allows a lot of solution with different time asymptotic. Let's describe a solution in .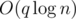

Let's first consider a problem with only queries of second and third type. It can be solved in the following manner. Consider a line consisting of all employees from 1 to n. An observation: any department looks like a contiguous segment of workers. Let's keep those segments in any logarithmic data structure like a balanced binary search tree (std::set or TreeSet). When merging departments from x to y, just extract all segments that are in the range [x, y] and merge them. For answering a query of the third type just check if employees x and y belong to the same segment. In such manner we get a solution of an easier problem in $O(\log n)$ per query.

Q1: 怎样用 std::set 在 $O(\log n)$ 的时间内将 $[x, y]$ 范围内的 segments 提取出来并且合并呢？

When adding the queries of a first type we, in fact, allow some segments to correspond to the same department. Let's add a DSU for handling equivalence classes of segments. Now the query of the first type is just using merge inside DSU for departments which x and y belong to. Also for queries of the second type it's important not to forget to call merge from all extracted segments.

So we get a solution in $ O(q(\log n + \alpha(n))) = O(q\log n)$ time.

正如题解所说，若果只考虑2，3两种操作，那么用线段树维护区间就可以了（当然还可以按别种方式维护，但我第一个想到的就是线段树）。我们来考虑这个extract all segments that are in the range [x, y] and merge them要怎么写。线段树的本质就是4个字——维护区间。维护区间做何用呢？答曰：查询任意区间I的某种信息 (information) INFO(I)或者也可称为区间I的某种性质(property)P(I)。概括起来就是通过维护有限个节点(区间)的某些信息从而支持对任意区间的某些信息的查询。线段树的查询就是个提取(extract)区间信息的过程:

Query(id, L, R, l, r)就是提取目标区间(l, r)与节点(L, R)的交集(max(l, L), min(r, R))的信息。如果(L, R)含有我们所需的关于(max(l, L), min(r, R))的信息，则直接返回这些信息，否则要向下分治。

//extract info. of target subsegment within node (L, R)
int extract(int id, int L, int R, int l, int r){
	if(tag[id]){
		return tag[id];
	}
	else{
		int mid=(L+R)>>, s1=, s2=, res;
		if(l<=mid)
			s1=extract(id<<, L, mid, l, r);
		if(r>mid)
			s2=extract(id<<|, mid+, R, l, r);
		res=s1?s1:s2;
		if(l<=L&&R<=r)
			tag[id]=res;
		return res;
	}
}

但这个写法是错的，和Tutorial的描述不相符，并没有把(l, r)的旧区间(departments)合并。

int query(int id, int L, int R, int pos){
	if(tag[id]) return tag[id];
	int mid=(L+R)>>;
	if(pos<=mid)
		return query(id<<, L, mid, pos);
	return query(id<<|, mid+, R, pos);
}
//extract info. of target subsegment within node (L, R)
void extract(int id, int L, int R, int l, int r, int label){
	if(tag[id]){
		tag[id]=label;
	}
	else{
		if(l<=L&&R<=r)
			tag[id]=label;
		else{
			int mid=(L+R)>>;
			if(l<=mid)
				extract(id<<, L, mid, l, r, label);
			if(r>mid)
				extract(id<<|, mid+, R, l, r, label);
		}
	}
}

这样才是正确的姿势。

another version

int query(int id, int L, int R, int pos){
	if(tag[id]) return tag[id];
	int mid=(L+R)>>;
	if(pos<=mid)
		return query(id<<, L, mid, pos);
	return query(id<<|, mid+, R, pos);
}
//extract info. of target subsegment within node (L, R)
void extract(int id, int L, int R, int l, int r, int label){
	if(tag[id]){
		tag[id]=label;
	}
	else{
		if(l<=L&&R<=r)
			tag[id]=label;
		else{
			int mid=(L+R)>>;
			if(l<=mid)
				extract(id<<, L, mid, l, r, label);
			if(r>mid)
				extract(id<<|, mid+, R, l, r, label);
			if(tag[id<<]==tag[id<<|])
				tag[id]=tag[id<<];
		}
	}
}

最后一句

if(tag[id<<1]==tag[id<<1|1])

tag[id]=tag[id<<1];

不清楚要不要加上

---

现在看 Tutorial 的第三段，为了支持操作1，再加上一个并查集（DSU）来维护不同区间之间的等价性(equivalence)

注意要将取出的旧区间合并，开始我是这么写的：

#include<bits/stdc++.h>
using namespace std;
const int MAX_N=2e5+;
//DSU
int par[MAX_N];
void init(int n){
	for(int i=; i<=n; i++)
		par[i]=i;
}
int find(int x){
	int root=x;
	while(par[root]!=root)
		root=par[root];
	int tmp;
	while(par[x]!=x){
		tmp=par[x];
		par[x]=root;
		x=tmp;
	}
	return root;
}
void unite(int x, int y){
	x=find(x);
	y=find(y);
	par[x]=y;
}
//ST
int tag[MAX_N<<];
void build(int id, int l, int r){
	if(l==r)
		tag[id]=l;
	else{
		int mid=(l+r)>>;
		build(id<<, l, mid);
		build(id<<|, mid+, r);
	}
}
int query(int id, int L, int R, int pos){
	if(tag[id])
		return tag[id];
	int mid=(L+R)>>;
	if(pos<=mid)
		return query(id<<, L, mid, pos);
	return query(id<<|, mid+, R, pos);
}
void extract(int id, int L, int R, int l, int r, int lable){
	if(tag[id]){
		unite(tag[id], lable);//extract old segments
		tag[id]=lable;
	}
	else{
		int mid=(L+R)>>;
		if(l<=mid)
			extract(id<<, L, mid, l, r, lable);
		if(r>mid)
			extract(id<<|, mid+, R, l, r, lable);
		if(tag[id>>]==tag[id>>|])
			tag[id]=tag[id>>];
	}
}

int main(){
	//freopen("in", "r", stdin);
	int n, q;
	scanf("%d%d", &n, &q);
	init(n);
	build(, , n);
	int type, x, y, sx, sy;
	while(q--){
		scanf("%d%d%d", &type, &x, &y);
		switch(type){
			case :
				sx=query(, , n, x);
				sy=query(, , n, y);
				if(sx!=sy)
					unite(sx, sy);
				break;
			case :
				sx=query(, , n, x);
				extract(, , n, x, y, sx);
				break;
			case :
				sx=query(, , n, x);
				sy=query(, , n, y);
				//printf("%d %d\n", sx, sy);
				puts(find(sx)==find(sy)?"YES":"NO");
				break;
		}
	}
	return ;
}

果断又 T 了，原因是我没有完全领会 Tutorial 的意思，完全按照里面讲的去写，其实完全没必要 query。

后来看到了 Codeforces 的一个 AC 代码，短得～

#include<cstdio>
const int N=2e5+;
int f[N],next[N];
int find(int x){return x==f[x]?x:(f[x]=find(f[x]));}
void Union(int a,int b){f[find(a)]=find(b);}
int n,q;
int main()
{
		scanf("%d%d",&n,&q);
		for(int i=;i<=n;i++)
		{
				f[i]=i;
				next[i]=i+;
		}
		while(q--)
		{
				int a,b,c;
				scanf("%d%d%d",&a,&b,&c);
				if(a==) Union(b,c);
				else if(a==)
				{
						int fa = find(c);
						for(int i=b;i<=c;)
						{
								f[find(i)]=fa;
								int tmp=i;
								i=next[i];
								next[tmp]=next[c];
						}
				}
				else if(a==) puts(find(b)==find(c)?"YES":"NO");
		}
}

看过后明白了题解中“Also for queries of the second type it's important not to forget to call merge from all extracted segments.”的真正含义。在取出旧区间时，要将它们合并起来，这样查询的时候就不用先query员工所在的区间，再到DSU里面查询两个区间是否属于同一集合 (department) 了，直接判断两人的id是否在同一集合中就好了。

然后正确的写法是

#include<bits/stdc++.h>
using namespace std;
const int MAX_N=2e5+;
//DSU
int par[MAX_N];
void init(int n){
	for(int i=; i<=n; i++)
		par[i]=i;
}
int find(int x){
	int root=x;
	while(par[root]!=root)
		root=par[root];
	int tmp;
	while(par[x]!=x){
		tmp=par[x];
		par[x]=root;
		x=tmp;
	}
	return root;
}
void unite(int x, int y){
	par[find(x)]=find(y);
}
//ST
int tag[MAX_N<<];
void build(int id, int l, int r){
	if(l==r)
		tag[id]=l;
	else{
		int mid=(l+r)>>;
		build(id<<, l, mid);
		build(id<<|, mid+, r);
	}
}
//extract info. of target subsegment within node (L, R)
int extract(int id, int L, int R, int l, int r){
	if(tag[id]){
		return tag[id];
	}
	else{
		int mid=(L+R)>>, s1=, s2=, res;
		if(l<=mid)
			s1=extract(id<<, L, mid, l, r);
		if(r>mid)
			s2=extract(id<<|, mid+, R, l, r);
		if(s1&&s2){
			unite(s1, s2);
			res=s1;
		}
		else res=s1^s2;
		if(l<=L&&R<=r)
			tag[id]=res;
		return res;
	}
}

int main(){
	//freopen("in", "r", stdin);
	int n, q;
	scanf("%d%d", &n, &q);
	init(n);
	build(, , n);
	int type, x, y;
	while(q--){
		scanf("%d%d%d", &type, &x, &y);
		switch(type){
			case :
				unite(x, y);
				break;
			case :
				extract(, , n, x, y);
				break;
			case :
				puts(find(x)==find(y)?"YES":"NO");
				break;
		}
	}
	return ;
}

---

总结

看了题解后，感觉我开始的思路是对的，就是在如何处理操作2上没有想到好办法。参考题解给出的区间+DSU解法时，反而受到误导。最后发现这道题其实还是一道并查集的题，线段树只是用来辅助操作2的区间合并的（题解描述的貌似刚好相反）。

那种相当短的写法恐怕是一种别人都知道我还不知道的 practice，必须学习一下，但是其复杂度恐怕不是 $q\log(n)$，极有可能还要低些，线段树写法的复杂度是 $q\log(n)$ 无疑。

但线段树还是处理区间问题一种普适工具，应该 get 到其精髓，学会灵活运用。

---

EDIT 2018/3/29

今天再来看这篇随笔已经看不懂了，当初写的太乱了。