Make It Equal 题解

Problem Link

简要题意

翻译很清楚。

思路

提供一种简单直接的思路。

可以发现最多会操作 \(n\) 次。

那么就可以每次直接枚举切的高度 \(h\)，检查更改是否超过 \(k\)，之后暴力修改这一段，然后重复以上步骤。

但是直接这样做是 \(\mathcal{O}(n^3)\)。

发现需要维护区间和，那么就可以直接使用线段树维护，寻找比 \(h\) 大的数可以使用二分（将原数组排序，在线段树上用单点查询二分），修改操作使用线段树推平，只修改比 \(h\) 大的数并不影响单调性所以可以重复以上操作。

这样复杂度就是 \(\mathcal{O}(n \log^3{n})\)，因为需要单点查询所以多了一个 \(\mathcal{O}(\log{n})\)。

然后继续考虑优化。

如图：

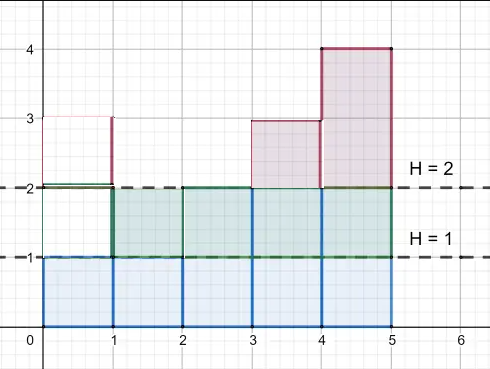
发现可以递推出切高度 \(h\) 的贡献开始部分。

记录 \(pos_i\) 为切高度 \(i\) 时贡献开始的位置。

例如上图中，\(pos_1 = 1,pos_2=2,pos_3=4,pos_4=5\)。

切成高度 \(h\) 后，\(pos_i (i \in [1,h-1])\) 并不受影响。

然后复杂度就只有 \(\mathcal{O}(n \log^2{n})\)，顺利通过。

code

#include <cstdio>
#include <queue>
#include <cstring>
#include <vector>
#include <algorithm>
#include <ctype.h>

using i64 = long long ;

const int N = 2e5 + 5 ;

char *p1,*p2,buf[1<<20];
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
inline i64 read(){
    i64 x=0,fh=1;
    char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')fh=-1;ch=getchar();}
    while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    return x*fh;
}
void Write(i64 x){
    if(x>9)Write(x/10);
    putchar(x%10+'0');
}
inline void write(i64 x){
    if(x<0)putchar('-'),x=-x;
    Write(x);
}

int n;
i64 k;
i64 a[N],minn = 0x7fffffffff;

struct SegmentTree{
    int lazy[N<<2];
    i64 sum[N<<2];

    void build(int k = 1,int l = 1,int r = n) {
        if(l == r) {sum[k] = a[l];return;}

        int mid = l+r>>1;
        build(k<<1,l,mid);
        build(k<<1|1,mid+1,r);

        sum[k] = sum[k<<1] + sum[k<<1|1];
    }

    void pushdown(int k,int l,int r) {
        if(!lazy[k]) return;

        int mid = l+r>>1;

        sum[k<<1] = (mid-l+1)*lazy[k];
        sum[k<<1|1] = (r-mid) * lazy[k];

        lazy[k<<1] = lazy[k];
        lazy[k<<1|1] = lazy[k];

        lazy[k] = 0;
    }

    i64 QuerySum(int k,int l,int r,int x,int y) {
        if(x <= l && r <= y) return sum[k];

        pushdown(k,l,r);

        int mid = l+r>>1;

        i64 val = 0;

        if(x <= mid)
            val += QuerySum(k<<1,l,mid,x,y);
        if(y > mid)
            val += QuerySum(k<<1|1,mid+1,r,x,y);

        return val;
    }

    void change(int k,int l,int r,int x,int y,i64 val) {
        if(x <= l && r <= y) {
            sum[k] = (r-l+1)*val;
            lazy[k] = val;
            return;
        }

        pushdown(k,l,r);

        int mid = l+r>>1;

        if(x <= mid)
            change(k<<1,l,mid,x,y,val);
        if(y > mid)
            change(k<<1|1,mid+1,r,x,y,val);

        sum[k] = sum[k<<1] + sum[k<<1|1];
    }
}t;//优化1 线段树

int pos[N];
bool check(int mid){

    int x = pos[mid];

    if(x == n+1) return 1;

    return t.QuerySum(1,1,n,x,n) - (i64)mid * (n-x+1) <= k;
}

int main(){

    n=read(),k=read();

    for(int i = 1; i <= n; i++) {
        a[i] = read();
        minn = std::min(minn,a[i]);//最后所有数一定是最小的
    }

    std::sort(a+1,a+n+1);

    for(int i = 1; i <= n; i++)
        if(pos[a[i]]) pos[a[i]] = std::min(pos[a[i]],i);//注意细节
        else pos[a[i]] = i;

    for(int i = 200000; i; i--)
        if(!pos[i]) pos[i] = pos[i+1]; // 记录切高度i时贡献从哪开始

    t.build();

    int ans = 0;
    while(true) {

        if(t.QuerySum(1,1,n,1,n) == minn * n) break;

        int l = minn, r = 200000;
        int x = -1;

        while(l <= r) {
            int mid = l+r>>1;

            if(check(mid)) r = mid-1,x=mid;
            else l = mid+1;
        }

        if(x == -1) break;

        ans++;

        t.change(1,1,n,pos[x],n,x);//区间推平操作
    }

    write(ans);
    return 0;
}