DARTS：基于梯度下降的经典网络搜索方法，开启端到端的网络搜索 | ICLR 2019

DARTS是很经典的NAS方法，它的出现打破了以往的离散的网络搜索模式，能够进行end-to-end的网络搜索。由于DARTS是基于梯度进行网络更新的，所以更新的方向比较准确，搜索时间相当于之前的方法有很大的提升，CIFAR-10的搜索仅需要4GPU days。

 

来源：晓飞的算法工程笔记 公众号

论文: DARTS: Differentiable Architecture Search

• 论文地址：https://arxiv.org/abs/1806.09055
• 论文代码：https://github.com/quark0/darts

Introduction

---

  目前流行的神经网络搜索方法大都是对离散的候选网络进行选择，而DARTS则是对连续的搜索空间进行搜索，并根据验证集的表现使用梯度下降进行网络结构优化，论文的主要贡献如下：

• 基于bilevel优化提出创新的gradient-based神经网络搜索方法DARTS，适用于卷积结构和循环结构。
• 通过实验表明gradient-based结构搜索方法在CIFAR-10和PTB数据集上都有很好的竞争力。
• 搜索性能很强，仅需要少量GPU days，主要得益于gradient-based优化模式。
• 通过DARTS在CIFAR-10和PTB上学习到的网络能够转移到大数据集ImageNet和WikiText-2上。

Differentiable Architecture Search

---

Search Space

  DARTS的整体搜索框架跟NASNet等方法一样，通过搜索计算单元(cell)的作为网络的基础结构，然后堆叠成卷积网络或者循环网络。计算单元是个有向无环图，包含\(N\)个节点的有序序列，每个节点\(x^{(i)}\)代表网络的中间信息(如卷积网络的特征图)，边代表对\(x^{(i)}\)的操作\(o^{(i,j)}\)。每个计算单元有两个输入和一个输出，对于卷积单元，输入为前两层的计算单元的输出，对于循环网络，输入则为当前step的输入和前一个step的状态，两者的输出均为将中间节点的所有输出进行合并操作。每个中间节点的计算基于前面所有的节点：

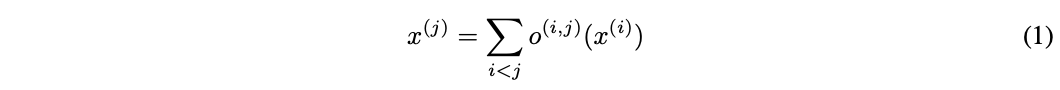
  这里包含一个特殊的zero操作，用来指定两个节点间没有连接。DARTS将计算单元的学习转换为边操作的学习，整体搜索框架跟NASNet等方法一样，本文主要集中在DARTS如何进行gradient-based的搜索。

Continuous Relaxation and Optimization

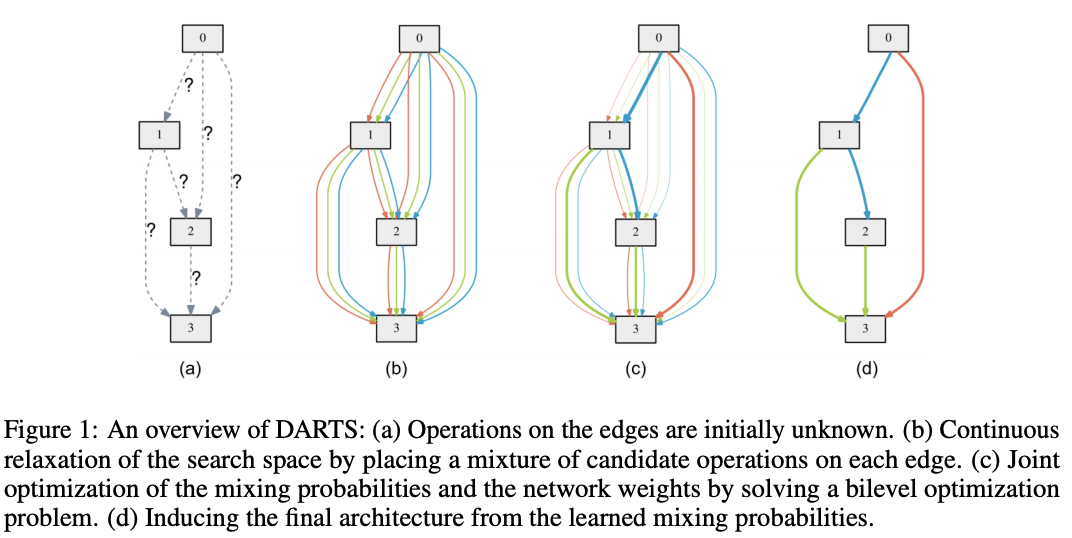
  让\(O\)为候选操作集，每个操作代表应用于\(x^{(i)}\)的函数\(o(\cdot)\)，为了让搜索空间连续化，将原本的离散操作选择转换为所有操作的softmax加权输出：

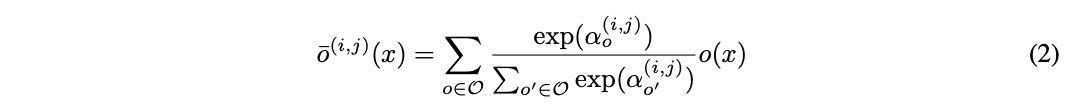
  节点\((i,j)\)间的操作的混合权重表示为维度\(|O|\)的向量\(\alpha^{(i,j)}\)，整个架构搜索则简化为学习连续的值\(\alpha=\{\alpha^{(i, j)}\}\)，如图1所示。在搜索的最后，每个节点选择概率最大的操作\(o^{(i,j)}=argmax_{o\in O}\alpha^{(i,j)}_o\)代替\(\bar{o}^{(i,j)}\)，构建出最终的网络。

  在简化后，DARTS目标是够同时学习网络结构\(\alpha\)和所有的操作权值\(w\)。对比之前的方法，DARTS能够根据验证集损失使用梯度下降进行结构优化。定义\(\mathcal{L}_{train}\)和\(\mathcal{L}_{val}\)为训练和验证集损失，损失由网络结构\(\alpha\)和网络权值\(w\)共同决定，搜索的最终目的是找到最优的\(\alpha^{*}\)来最小化验证集损失\(\mathcal{L}_{val}(w^{*}, \alpha^{*})\)，其中网络权值\(w^{*}\)则是通过最小化训练损失\(w^{*}=argmin_w \mathcal{L}_{train}(w, \alpha^{*})\)获得。这意味着DARTS是个bilevel优化问题，使用验证集优化网络结构，使用训练集优化网络权重，\(\alpha\)为上级变量，\(w\)为下级变量：

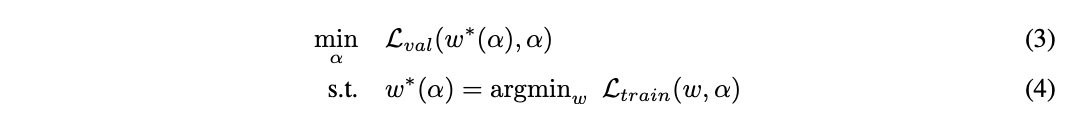
Approximate Architecture Gradient

  公式3计算网络结构梯度的开销是很大的，主要在于公式4的内层优化，即每次结构的修改都需要重新训练得到网络的最优权重。为了简化这一操作，论文提出了提出了简单的近似的改进：

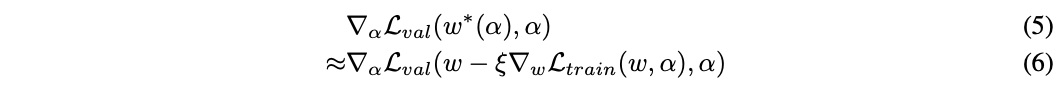
  \(w\)表示当前的网络权重，\(\xi\)是内层优化单次更新的学习率，整体的思想是在网络结构改变后，通过单次训练step优化\(w\)来逼近\(w^{(*)}(\alpha)\)，而不是公式3那样需要完整地训练直到收敛。实际当权值\(w\)为内层优化的局部最优解时(\(\nabla_{w}\mathcal{L}_{train}(w, \alpha)=0\))，公式6等同于公式5\(\nabla_{\alpha}\mathcal{L}_{val}(w, \alpha)\)。

  迭代的过程如算法1，交替更新网络结构和网络权重，每次的更新都仅使用少量的数据。根据链式法则，公式6可以展开为：

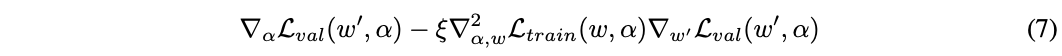
  \(w^{'}=w - \xi \nabla_w \mathcal{L}_{train}(w, \alpha)\)，上述的式子的第二项计算的开销很大，论文使用有限差分来近似计算，这是论文很关键的一步。\(\epsilon\)为小标量，\(w^{\pm}=w\pm \epsilon \nabla_{w^{'}} \mathcal{L}_{val}(w^{'}, \alpha)\)，得到：

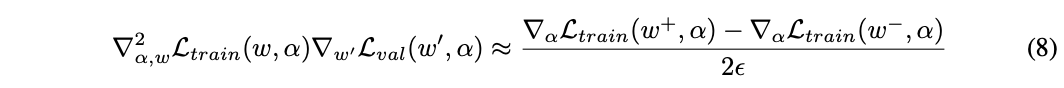
  计算最终的差分需要两次正向+反向计算，计算复杂度从\(O(|\alpha| |w|)\)简化为\(O(|\alpha|+|w|)\)。

• First-order Approximation

  当\(\xi=0\)时，公式7的二阶导会消失，梯度由\(\nabla_{\alpha}\mathcal{L}(w, \alpha)\)决定，即认为当前权值总是最优的，直接通过网络结构修改来优化验证集损失。\(\xi=0\)能加速搜索的过程，但也可能会带来较差的表现。当\(\xi=0\)时，论文称之为一阶近似，当\(\xi > 0\)时，论文称之为二阶近似。

Deriving Discrete Architectures

  在构建最终的网络结构时，每个节点选取来自不同节点的top-k个响应最强的非zero操作，响应强度通过\(\frac{exp(\alpha^{(i,j)_o})}{\sum_{o^{'}\in O}exp(\alpha^{(i,j)}_{o^{'}})}\)计算。为了让搜索的网络性能更好，卷积单元设置\(k=2\)，循环单元设置\(k=1\)。过滤zero操作主要让每个节点有足够多的输入，这样才能与当前的SOTA模型进行公平比较。

Experiments and Results

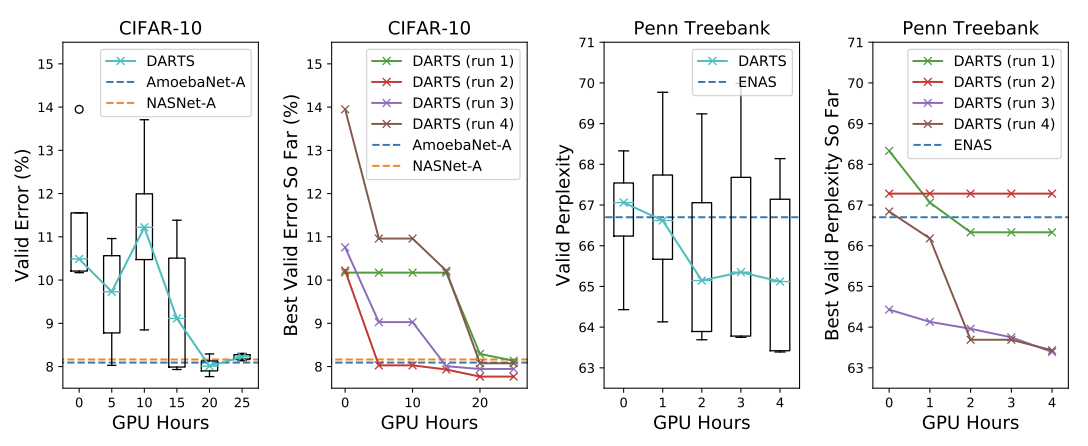
  搜索耗时，其中run代表多次搜索取最好的结果。

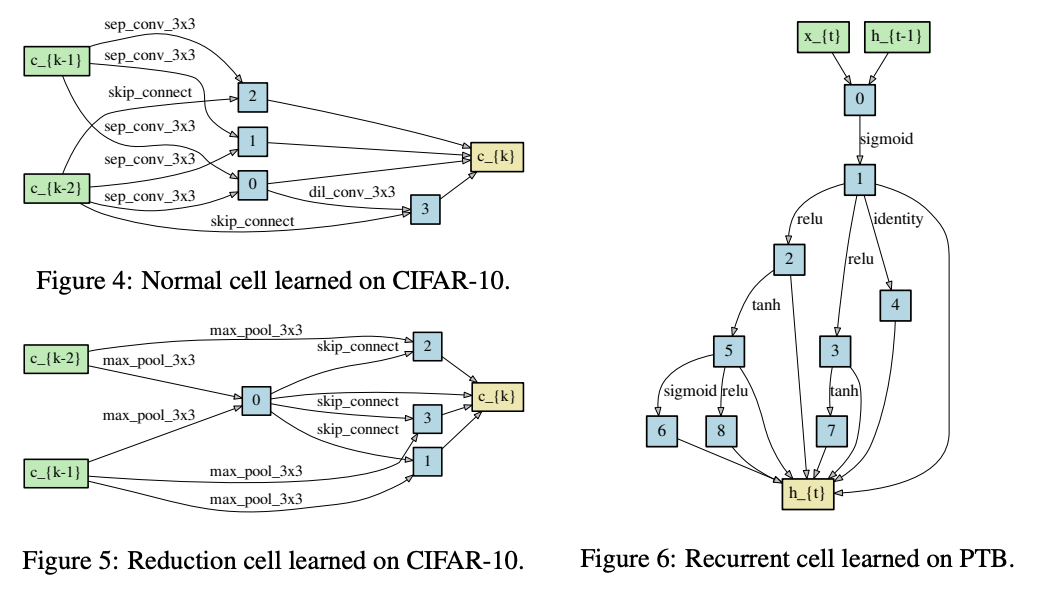
  搜索到的结构。

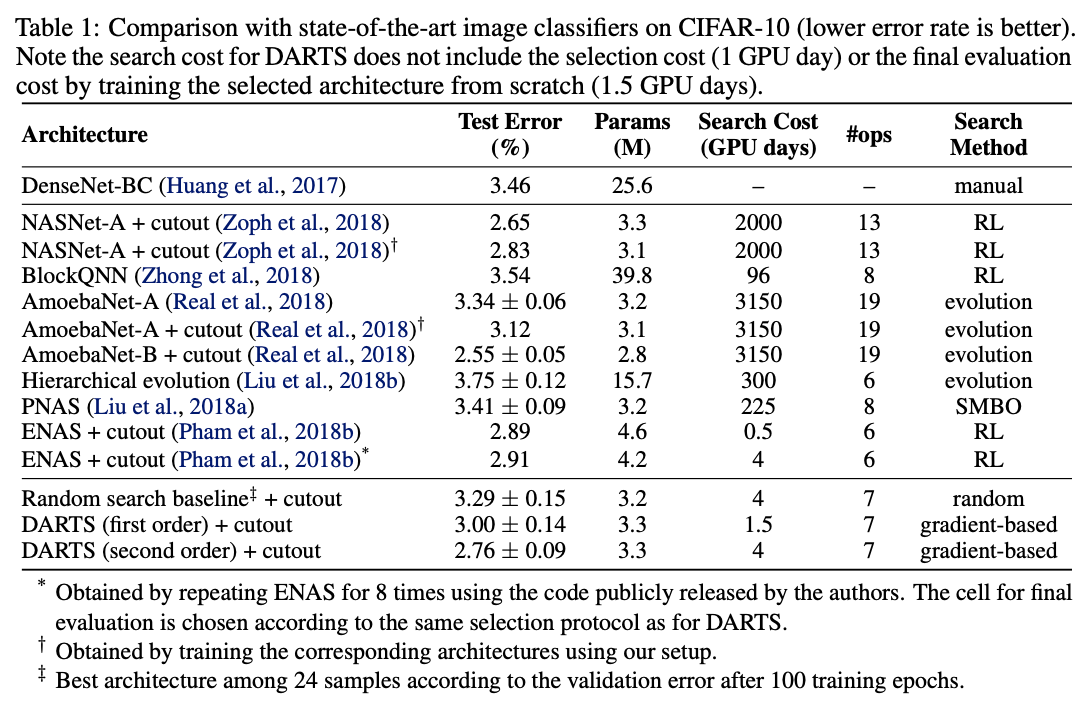
  CIFAR-10上的性能对比。

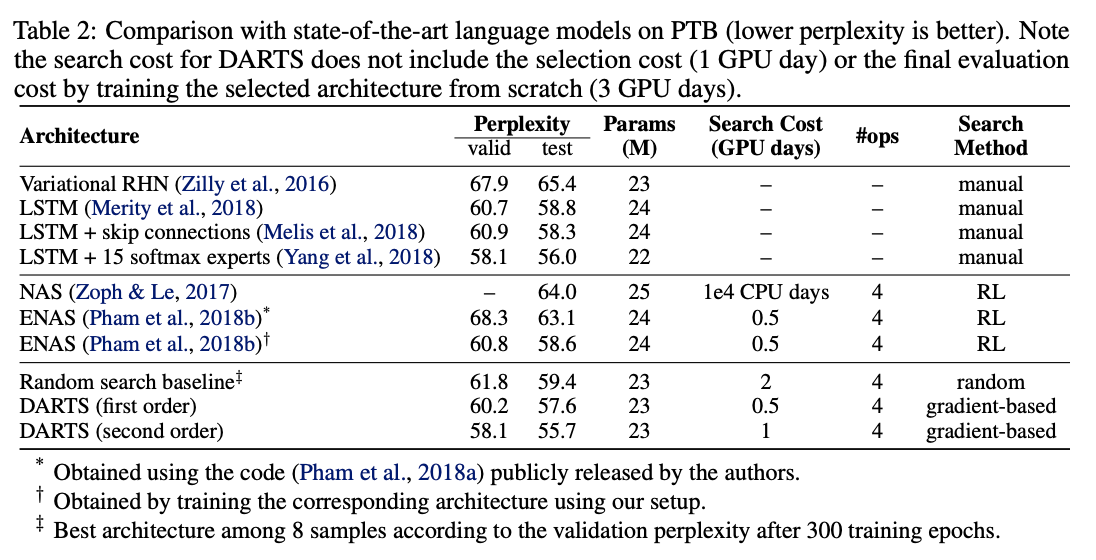
  PTB上的性能对比。

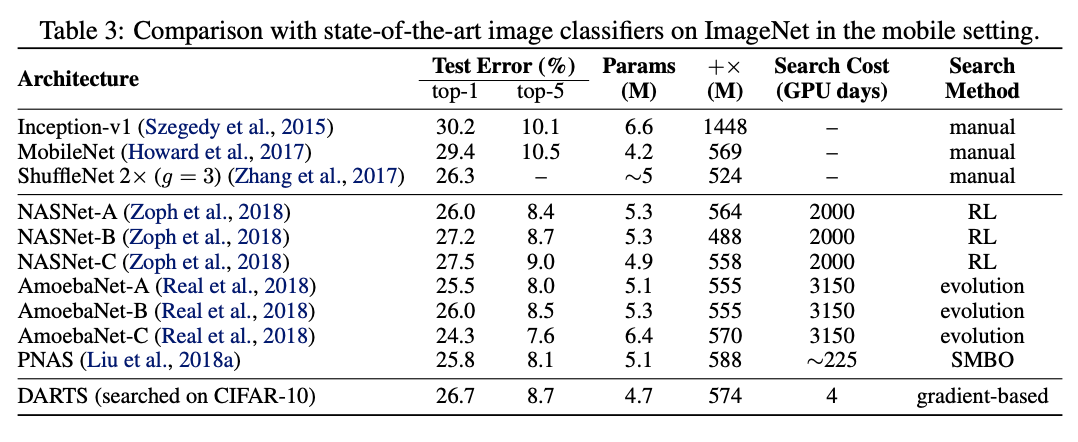
  迁移到ImageNet上的性能对比。

Conclustion

---

  DARTS是很经典的NAS方法，它的出现打破了以往的离散的网络搜索模式，能够进行end-to-end的网络搜索。由于DARTS是基于梯度进行网络更新的，所以更新的方向比较准确，搜索时间相当于之前的方法有很大的提升，CIFAR-10的搜索仅需要4GPU days。

 

 

 

如果本文对你有帮助，麻烦点个赞或在看呗～

更多内容请关注 微信公众号【晓飞的算法工程笔记】