重新整理数据结构与算法(c#)——算法套路迪杰斯特拉算法[三十一]
前言
迪杰斯特拉算法 是求最短路径方法的其中一种,这个有什么作用呢?
有一张图:
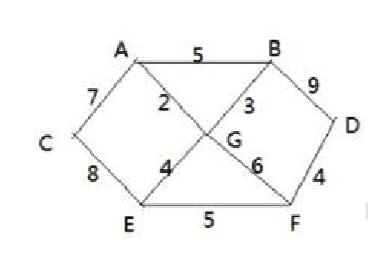
假设求G点到其他各点的最小路径。
是这样来的。
比如找到了和G点相连接所有点,ABED。这时候确定GA是一定是最短的,为什么这么说呢?G->A和G从别的点到A,一旦G走BED 一定会大于GA,后续就跟不可能大于了。
所以GA为最短,这时候就确定了A。这时候开始从A点开始,找到和A点相连但是没有确定最短的点,有B、C。G->A->B 大于G->B。然后A可以到C,这时候确定G->C 是9。
然后从G到各点已经相连中,找到没有确认的最小路径,这个就是确认了G->B最短。为什么能够确认呢?因为G到A然后到B大于G->B,那么可以确认G到B最短,这是因为GA是最短的,从最短的到不了,其他的一定大于G->B。
上面说其实有点模糊。
是这样的,如果从G为出发点确认了n个点,那么剩下的m个点怎么确认呢?
肯定就是从G从到先到G最短的点,尝试是否有其他路,如果没有,那么就确认了。
正文
代码如下:
class Program
{
private static int INF = int.MaxValue;
static void Main(string[] args)
{
char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
int N = 65535;// 表示不可以连接
int[,] matrix = { { N, 5, 7, N, N, N, 2 },
{ 5, N, N, 9, N, N, 3 },
{ 7, N, N, N, 8, N, N },
{ N, 9, N, N, N, 4, N },
{ N, N, 8, N, N, 5, 4 },
{ N, N, N, 4, 5, N, 6 },
{ 2, 3, N, N, 4, 6, N }
};
//创建 Graph对象
Graph graph = new Graph(vertex, matrix);
//测试, 看看图的邻接矩阵是否ok
graph.showGraph();
//测试迪杰斯特拉算法
graph.dsj(2);//C
graph.showDijkstra();
Console.Read();
}
}
class Graph
{
private char[] vertex;//顶点数组
private int[,] matrix;//邻接矩阵
private VisitedVertex vv;//顶点状态
public Graph(char[] vertex, int[,] matrix)
{
this.vertex = vertex;
this.matrix = matrix;
}
public void showDijkstra()
{
vv.show();
}
public void showGraph()
{
for (int i = 0; i < vertex.Length; i++)
{
for (int j = 0; j < vertex.Length; j++)
{
Console.Write(matrix[i, j] + " ");
}
Console.WriteLine();
}
}
public void dsj(int index)
{
vv = new VisitedVertex(vertex.Length, index);
update(index);
for (int i = 1; i < vertex.Length; i++)
{
index = vv.updateArr();
update(index);
}
}
private void update(int index)
{
int len = 0;
for (int j = 0; j < vertex.Length; j++)
{
len = vv.getDis(index) + matrix[index, j];
if (!vv.isVisited(j) && len < vv.getDis(j))
{
vv.updatePre(j, index);
vv.updateDis(j, len);
}
}
}
}
class VisitedVertex
{
//记录各个顶点的访问状态
public int[] already_arr;
//每个顶点对应前一个顶点的下标
public int[] pre_visited;
//记录出发点到其他顶点的距离
public int[] dis;
public VisitedVertex(int length, int index)
{
already_arr = new int[length];
pre_visited = new int[length];
dis = new int[length];
Array.Fill(dis, int.MaxValue);
this.already_arr[index] = 1;
this.dis[index] = 0;
}
public int updateArr()
{
int min = int.MaxValue, index = 0;
for (int i = 0; i < already_arr.Length; i++)
{
if (already_arr[i] == 0 && dis[i] < min)
{
min = dis[i];
index = i;
}
}
//更新 index 顶点被访问过
already_arr[index] = 1;
return index;
}
/// <summary>
/// 是否访问过
/// </summary>
/// <param name="index">下标距离</param>
/// <returns></returns>
public Boolean isVisited(int index)
{
return already_arr[index] == 1;
}
//更新距离
public void updateDis(int index, int length)
{
dis[index] = length;
}
//更新前驱节点
public void updatePre(int index, int pre)
{
pre_visited[index] = pre;
}
//返回到某个节点的距离
public int getDis(int index)
{
return dis[index];
}
//显示最后的结果
//即将三个数组的情况输出
public void show()
{
Console.WriteLine("输出前驱");
//输出pre_visited
foreach (int i in pre_visited)
{
Console.Write(i + " ");
}
Console.WriteLine();
char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
int count = 0;
foreach (int i in dis)
{
if (i != 65535)
{
Console.Write(vertex[count] + "(" + i + ") ");
}
else
{
Console.Write("N ");
}
count++;
}
Console.WriteLine();
}
}
结果:
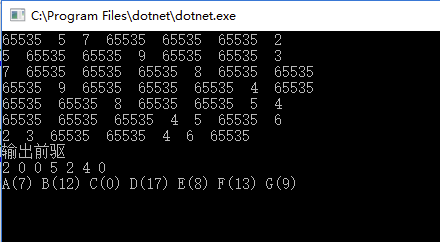
重新整理数据结构与算法(c#)——算法套路迪杰斯特拉算法[三十一]的更多相关文章
- C++迪杰斯特拉算法求最短路径
一:算法历史 迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法.是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题.迪杰斯特拉算法主要特点是以 ...
- 图(最短路径算法————迪杰斯特拉算法和弗洛伊德算法).RP
文转:http://blog.csdn.net/zxq2574043697/article/details/9451887 一: 最短路径算法 1. 迪杰斯特拉算法 2. 弗洛伊德算法 二: 1. 迪 ...
- 算法与数据结构(六) 迪杰斯特拉算法的最短路径(Swift版)
上篇博客我们详细的介绍了两种经典的最小生成树的算法,本篇博客我们就来详细的讲一下最短路径的经典算法----迪杰斯特拉算法.首先我们先聊一下什么是最短路径,这个还是比较好理解的.比如我要从北京到济南,而 ...
- [从今天开始修炼数据结构]图的最短路径 —— 迪杰斯特拉算法和弗洛伊德算法的详解与Java实现
在网图和非网图中,最短路径的含义不同.非网图中边上没有权值,所谓的最短路径,其实就是两顶点之间经过的边数最少的路径:而对于网图来说,最短路径,是指两顶点之间经过的边上权值之和最少的路径,我们称路径上第 ...
- 数据结构---公交线路提示系统05(内附读取表格+迪杰斯特拉算法Java代码)
今天做的最多的事情就是纠错了,通过添加输出语句判断错误来源: 找到错误来源: wb = new XSSFWorkbook(input);//语句创建错误 网上查询发现是jar包的问题: 下图为poi的 ...
- 迪杰斯特拉算法——PAT 1003
本文主要是将我对于我对于迪杰斯特拉算法的理解写出来,同时通过例题来希望能够加深对于算法的理解,其中有错误的地方希望大家指正. 迪杰斯特拉算法 我将这个算法理解成一个局部到整体的算法,这个方法确实越研究 ...
- 迪杰斯特拉算法c语言实现
/*http://1wangxiaobo@163.com 数据结构C语言版 迪杰斯特拉算法 P189 http://1wangxiaobo@163.com 编译环境:Dev-C++ 4.9.9.2 ...
- 最短路问题:迪杰斯特拉算法(Dijsktra)
Dijkstra算法 1.定义概览 Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径.主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止.Di ...
- 最短路径之迪杰斯特拉算法的Java实现
Dijkstra算法是最短路径算法中为人熟知的一种,是单起点全路径算法.该算法被称为是“贪心算法”的成功典范.本文接下来将尝试以最通俗的语言来介绍这个伟大的算法,并赋予java实现代码. 一.知识准备 ...
- 数据结构图之三(最短路径--迪杰斯特拉算法——转载自i=i++
数据结构图之三(最短路径--迪杰斯特拉算法) [1]最短路径 最短路径?别乱想哈,其实就是字面意思,一个带边值的图中从某一个顶点到另外一个顶点的最短路径. 官方定义:对于内网图而言,最短路径是指两 ...
随机推荐
- C++ //常用算术生成算法 //#include<numeric> accumulate //fill //向容器中填充指定的元素
1 //常用算术生成算法 //#include<numeric> accumulate 2 //fill //向容器中填充指定的元素 3 #include<iostream> ...
- 使用Zabbix监控openstack的系统资源
1 概述 OpenStack是一个开源的云计算管理平台项目,是一系列软件开源项目的组合.由NASA(美国国家航空航天局)和Rackspace合作研发并发起,以Apache许可证(Apache软件基金会 ...
- win10 有 休眠 功能,将内存保存到文件,开机10秒左右,恢复之前idea等所有软件
休眠 休眠 休眠 重要的事情说三遍. 提示,默认不显示,需要控制面板 电源里面设置下.
- Dashboard、Rancher与KubeSphere对比
在容器技术和微服务架构日益盛行的今天,对于容器编排和管理平台的选择显得尤为重要.Kubernetes(K8s)作为容器编排的事实标准,其生态系统中涌现出了许多管理和监控工具.其中,Dashboard. ...
- 【深度学习】批量归一化 BatchNormalization
一.背景 机器学习的本质是对物理世界进行建模,做的就是拟合数据分布. 但是在模型训练过程中,神经网络参数不断更新,导数中间层的数据分布频繁地变化(内部协变量偏移),不利于网络参数 ...
- 关于C++ 多态实现技术的深度解析(vfptr,vftable)
PS:要转载请注明出处,本人版权所有. PS: 这个只是基于<我自己>的理解, 如果和你的原则及想法相冲突,请谅解,勿喷. 前置说明 本文作为本人csdn blog的主站的备份.(Bl ...
- Djaong 运行报错:ValueError: Unable to configure handler 'default'
一.前提条件 1.Django 项目接入了 log 日志模块 二.解决方案 启动项目或者项目运行中,遇到如下报错 File "C:\Python38\lib\logging\config.p ...
- python基础六(函数基础及参数使用)
一. 函数定义 1.什么是函数 函数就相当于具备某一功能的工具 函数的使用必须遵循一个原则: 先定义 后调用2.为何要用函数 代码冗余,程序的组织结构不清晰,可读性差 可维护性.扩展性差3.如何用函数 ...
- 记录--关于无感刷新Token,我是这样子做的
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 什么是JWT JWT是全称是JSON WEB TOKEN,是一个开放标准,用于将各方数据信息作为JSON格式进行对象传递,可以对数据进行可 ...
- Java13版本特性【一文了解】
「MoreThanJava」 宣扬的是 「学习,不止 CODE」,本系列 Java 基础教程是自己在结合各方面的知识之后,对 Java 基础的一个总回顾,旨在 「帮助新朋友快速高质量的学习」. 当然 ...
