C#实现斐波拉切数列求和
C#实现斐波拉切数列求和
private void button1_Click(object sender, EventArgs e)
{
listBox1.Items.Clear();//清空ListBox控件
int p = 0, n = 0, a = 1, b = 1;//定义变量
try
{
p = Convert.ToInt32(textBox1.Text);//将字符型转换成数值型
}
catch//出现错误
{
MessageBox.Show("请输入数值型数据");//弹出提示框
textBox1.Text = "15";
return;
}
for (n = 1; n <= p; n++)//对输入的数值进行遍历
{
listBox1.Items.Add(a.ToString());//输出数值
listBox1.Items.Add(b.ToString());//输出数值
a = a + b;//获取前两个数的和
b = a + b;//获取前两个数的和
}
}
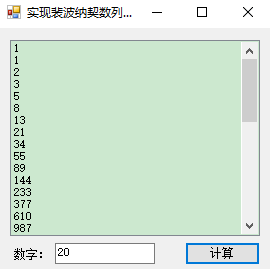
C#实现斐波拉切数列求和的更多相关文章
- Linux环境C语言斐波拉切数列(1,1,2,3,5,8,13,.........)实现
斐波那契数列(Fibonacci sequence),又称黄金分割数列.因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一 ...
- Python迭代器(斐波拉切数列实例)
将一个容器通过iter()函数处理后,就变成了迭代器.迭代器有2个魔法方法__iter__.__next__,一个迭代器必须实现__iter__,这个方法实际上是返回迭代器本身(return self ...
- hdu 2516(斐波拉切博弈)
题意:容易理解. 分析:通过枚举寻找规律,这就是做1堆或者2堆石子博弈的技巧!当为2或者3时,肯定是第二个人赢,当为4时,先去一个石子,然后当对方面临3,于是第一个人赢, 当为5时,取1时,第二个人赢 ...
- C语言数据结构----递归的应用(斐波拉契数列、汉诺塔、strlen的递归算法)
本节主要说了递归的设计和算法实现,以及递归的基本例程斐波拉契数列.strlen的递归解法.汉诺塔和全排列递归算法. 一.递归的设计和实现 1.递归从实质上是一种数学的解决问题的思维,是一种分而治之的思 ...
- 斐波拉契数列加强版——时间复杂度O(1),空间复杂度O(1)
对于斐波拉契经典问题,我们都非常熟悉,通过递推公式F(n) = F(n - ) + F(n - ),我们可以在线性时间内求出第n项F(n),现在考虑斐波拉契的加强版,我们要求的项数n的范围为int范围 ...
- 剑指offer三: 斐波拉契数列
斐波拉契数列是指这样一个数列: F(1)=1; F(2)=1; F(n)=F(n-1)+F(n); public class Solution { public int Fibonacci(int n ...
- 关于斐波拉契数列(Fibonacci)
斐波那契数列指的是这样一个数列 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10 ...
- 剑指offer-第二章算法之斐波拉契数列(青蛙跳台阶)
递归与循环 递归:在一个函数的内部调用这个函数. 本质:把一个问题分解为两个,或者多个小问题(多个小问题相互重叠的部分,会存在重复的计算) 优点:简洁,易于实现. 缺点:时间和空间消耗严重,如果递归调 ...
- 剑指offer-面试题9.斐波拉契数列
题目一:写一个函数,输入n,求斐波拉契数列的第n项. 斐波拉契数列的定义如下: { n=; f(n)={ n=; { f(n-)+f(n-) n>; 斐波拉契问题很明显我们会想到用递归来解决: ...
- [NEUQ-OJ] 1012 SZ斐波拉契数列
一道水题,让我看清基础我的基础是多么薄弱. 递归,数组清零,数组名/变量名重复层出不穷...路漫漫啊.......... http://ncc.neuq.edu.cn/oj/problem.php?i ...
随机推荐
- [计蒜客20191103B] 饮料
小 B 出门游玩,他现在走到了 \(n\) 家饮品店前,第 \(i\) 家买饮料的花费为$ cost_i$ ,他只能去花费不超过自己所带钱数额的店,但他现在不确定自己兜里有多少钱,所以现在给出 \(m ...
- CompletableFuture异步编程
1.创建 /** * public static <U> CompletableFuture<U> supplyAsync(Supplier<U> supplier ...
- Spring整合Quartz简单入门
创建一个Web项目 导入相关jar包 <?xml version="1.0" encoding="UTF-8"?> <project xmln ...
- 【最佳实践】京东小程序-LBS业务场景的性能提升
一.前言 1.1 京东LBS门详业务介绍 京东LBS门详目前已经支持了仓网.药急送.天选.小时达POP多种业务,并且具备了多端的能力,一套代码可以在京东app.健康app.微信小程序中运行,一定程度上 ...
- MySQL InnoDB加锁规则分析
1. 基础知识回顾 1.索引的有序性,索引本身就是有序的 2.InnoDB中间隙锁的唯一目的是防止其他事务插入间隙.间隙锁可以共存.一个事务取得的间隙锁并不会阻止另一个事务取得同一间隙上的间隙锁.共 ...
- 华企盾DSC半透明无法打开加密文件常见处理方法
1.查看客户端日志进程是否显示legal:1 2.半透明只支持双击打开 3.半透明进程不能设置HOOK白名单 4.检查调用的进程是否都加了 5.半透明程序的运行方式不可以以管理员启动,去掉" ...
- ASR项目实战-后处理
本文深入探讨后处理环节. 在本环节要处理的重要特性有分词.断句.标点符号.大小写.数字等的格式归一等. 分词 和NLP.搜索等场景下的分词含义不同.对于拼音类的语言,比如英语.法语等,句子由多个单词组 ...
- [VMware]ESXI下硬盘的两种直通方式
文章来自:https://rmbz.net/archives/vmware-esxi-passthrough 最近再搞ESXI,把原来的"黑群晖"改成ESXI:因为群晖里有数据,为 ...
- bazel test 编译失败:googletest、gtest 报错
问题描述 bazel test 遇到很多奇怪的编译错误,报错位置位于"googletest"目录,而且没有修改过 googletest 源码: ERROR: /bazel_cach ...
- LeetCode 分治篇(50、17)
50. Pow(x, n) 实现 pow(x, n) ,即计算 x 的 n 次幂函数. 示例 1: 输入: 2.00000, 10 输出: 1024.00000 示例 2: 输入: 2.10000, ...
