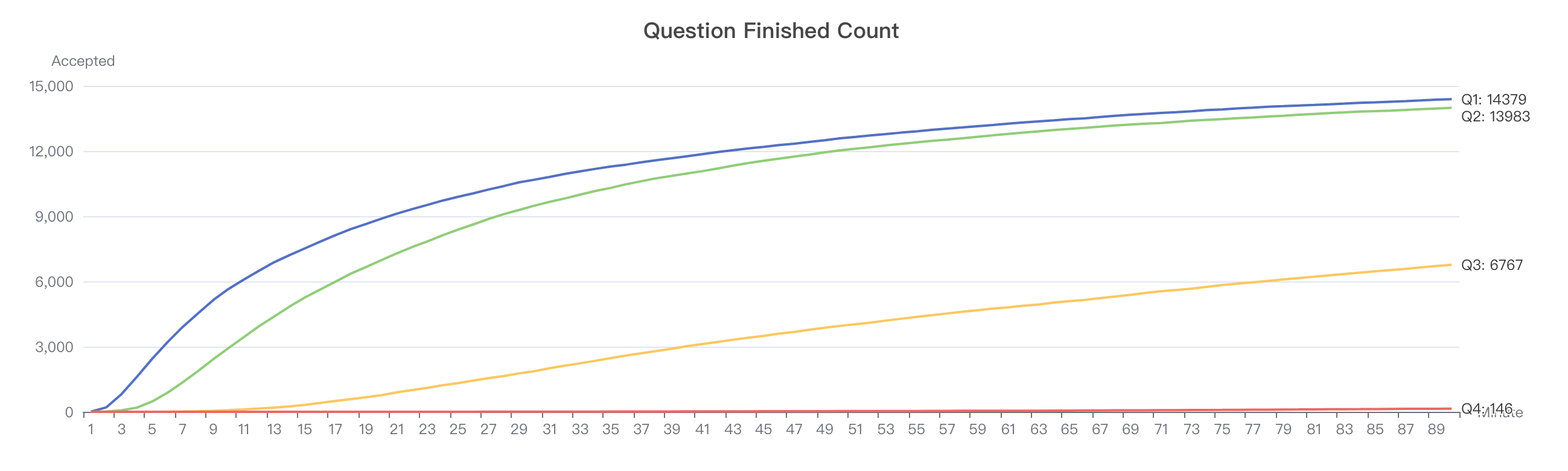
LeetCode 周赛 346（2023/05/21）仅 68 人 AK 的最短路问题

本文已收录到 AndroidFamily，技术和职场问题，请关注公众号 [彭旭锐] 提问。

• LeetCode 单周赛第 345 场 · 体验一题多解的算法之美

单周赛 345 概览

T1. 删除子串后的字符串最小长度（Easy）

标签：栈

T2. 字典序最小回文串（Medium）

标签：贪心、双指针

T3. 求一个整数的惩罚数（Medium）

标签：回溯、状态压缩、前缀和

T4. 修改图中的边权（Hard）

标签：贪心、最短路

---

T1. 删除子串后的字符串最小长度（Easy）

https://leetcode.cn/problems/minimum-string-length-after-removing-substrings/

题解（栈）

使用栈模拟扫描过程，当扫描到 D 和 B 时检查栈顶元素，最后栈内剩余的元素个数就是无法消除的最小长度：

class Solution {
    fun minLength(s: String): Int {
        val stack = ArrayDeque<Char>()
        for (c in s) {
            if (c == 'D' && stack.isNotEmpty() && stack.peek() == 'C') stack.pop()
            else if (c == 'B' && stack.isNotEmpty() && stack.peek() == 'A') stack.pop()
            else stack.push(c)
        }
        return stack.size
    }
}

复杂度分析：

• 时间复杂度：$O(n)$ 其中 n 为 s 字符串的长度；
• 空间复杂度：$O(n)$ 栈空间。

---

T2. 字典序最小回文串（Medium）

https://leetcode.cn/problems/lexicographically-smallest-palindrome/

题解（贪心）

贪心思路：当对称位置不相等时，只需要将其中一个位置修改到与另一个位置相同时，得到的操作次数是最少的：

class Solution {
    fun makeSmallestPalindrome(s: String): String {
        val arr = s.toCharArray()
        val n = s.length
        // 判断回文串写法
        for (i in 0 until n / 2) {
            val j = n - 1 - i
            if(arr[i] != arr[j]) {
                val temp = if(arr[i] < arr[j]) arr[i] else arr[j]
                arr[i] = temp
                arr[j] = temp
            }
        }
        return String(arr)
    }
}

复杂度分析：

• 时间复杂度：$O(n)$ 其中 n 为 s 字符串的长度；
• 空间复杂度：$O(n)$ 字符数组空间。

---

T3. 求一个整数的惩罚数（Medium）

https://leetcode.cn/problems/find-the-punishment-number-of-an-integer/

题解一（子集型回溯）

枚举每个数，使用子集型回溯检查是否存在满足条件的切分方案：

class Solution {
    fun punishmentNumber(n: Int): Int {
        if (n <= 3) return 1
        var ret = 0
        for (x in 4 .. n) {
            val target = x * x
            if (backTrack("$target", 0, x)) ret += target
        }
        return ret + 1 /* 1 满足条件 */
    }

    // 子集型回溯
    private fun backTrack(str : String, i : Int, target : Int) : Boolean {
        if (i == str.length) return target == 0
        var cur = 0
        for (to in i until str.length) {
            cur = cur * 10 + (str[to] - '0')
            if (backTrack(str, to + 1, target - cur)) return true
        }
        return false
    }
}

复杂度分析：

• 时间复杂度：$O(n^2)$ 每个数字 i 转字符串后的长度为 $log_i$，而枚举长度为 $log_i$ 的字符串的切分方案后 $2^{log_i}$ = i 种方案，因此整体的时间复杂度是 $O(n^2)$；
• 空间复杂度：$O(lgn)$ 递归栈空间。

题解二（状态压缩）

由于数字的长度小于 32，我们可以用 int 表示所有切分方案，再检查是否存在满足条件的切分方案：

class Solution {
    fun punishmentNumber(n: Int): Int {
        if (n <= 3) return 1
        var ret = 0
        for (x in 4 .. n) {
            val target = x * x
            if (check("$target", x)) ret += target
        }
        return ret + 1 /* 1 满足条件 */
    }

    // 状态压缩
    private fun check(str : String, target : Int) : Boolean {
        val m = str.length
        val upper = (1 shl m) - 1
        for (k in 1 .. upper) {
            var last = 0
            var sum = 0
            for (i in 0 until m) {
                val cur = str[i] - '0'
                if (k and (1 shl i) != 0) {
                    // 拆
                    sum += last
                    last = cur
                } else{
                    // 不拆
                    last = last * 10 + cur
                }
            }
            if (sum + last == target) return true
        }
        return false
    }
}

复杂度分析：

• 时间复杂度：同上；
• 空间复杂度：$O(1)$ 仅使用常量级别空间。

题解三（预处理 + 前缀和）

题解一和题解二在多个测试用例间会重复计算相同数字的切分方案，我们可以预处理 1 - 1000 中所有满足条件的数平方，并维护前缀和数组：

class Solution {

    companion object {
        private val U = 1000
        private val preSum = IntArray(U + 1)
        init {
            for (x in 4 .. U) {
                val target = x * x
                if (check("$target", x)) preSum[x] += target
                preSum[x] += preSum[x - 1]
            }
        }

        // 状态压缩
        private fun check(str : String, target : Int) : Boolean {
        }
    }

    fun punishmentNumber(n: Int): Int {
        return preSum[n] + 1
    }
}

复杂度分析：

• 时间复杂度：$O(U^2)$ 其中 U 是数据大小上界；
• 空间复杂度：$O(U)$ 前缀和数组空间。

---

T4. 修改图中的边权（Hard）

https://leetcode.cn/problems/modify-graph-edge-weights/submissions/434224996/

LeetCode 少有的难题，排进历史 Top 10 没问题吧？

问题无解的情况：

• 1、假设将所有负权边设置为 INF（2*10^9）时的最短路长度 dis < target（不论是否经过负权边），由于无法继续增大边权来增大最短路长度，因此问题无解；
• 2、假设将所有负权边设置为 1 时的最短路长度 dis > target（不论是否经过负权边），由于继续增大边权最短路不可能变小，因此问题无解。

错误的思路：

先把所有负权边设置为 1，再跑 Dijkstra 最短路，如果最短路长度 dis < target，那么将其中一条负权边继续增大 “target - dis”，就能是该路径的长度恰好为 target。然而，由于增加权重后最短路长度有可能变化，所以这个思路不能保证正确性。

正确的思路：

• 1、先把所有负权边改为 1 跑 Dijkstra 最短路，计算出起点到终点的最短路长度。同时，如果该长度 dis > target，则问题无解；如果该长度 dis == target，则直接返回；如果该长度 dis < target，则需要补全。
• 2、问题的关键在于，按什么顺序修改，以及修改到什么值。
  • 顺序：利用 Dijkstra 最短路算法每次使用「确定集」中最短路长度最短的节点去松弛其他点的时机，由于修改该点不会影响已确定路径，因此这是一个不错的时机；
  • 修改到什么值：需要满足 dis[0][x] + w + dis[y][e] = target，那么有 w = target - dis[0][x] - (dis[0][e] - dis[0][y]) = delta - dis[0][x] + dis[0][y]
• 3、虽然修改后最短路不一定经过 w，但由于不断的使用最短路长度最短的节点，因此最终总能修改成功，除非修改后最短路依然小于 target（例如存在直接从 s 到 e 的边）
• 4、最后，将未修改的边增加到 INF。

class Solution {

    private val INF = 1e9.toInt()

    fun modifiedGraphEdges(n: Int, edges: Array<IntArray>, source: Int, destination: Int, target: Int): Array<IntArray> {
        if (source !in 0 .. n - 1 || destination !in 0 .. n - 1) return edges
        if (source == destination || edges.isNullOrEmpty()) return edges
        // 建图（领接表，节点号 + 边号方便修改边权）
        val graph = Array(n) { ArrayList<IntArray>() }
        for ((i, edge) in edges.withIndex()) {
            graph[edge[0]].add(intArrayOf(edge[1], i))
            graph[edge[1]].add(intArrayOf(edge[0], i))
        }
        // 第一轮最短路
        val originDis = dijkstra1(graph, edges, source, destination)
        if (originDis[destination] > target) return emptyArray() // 无解
        // 第二轮最短路
        val delta = target - originDis[destination] // 需要补全的最短路
        val dis = dijkstra2(graph, edges, source, destination, delta, originDis)
        if (dis[destination] < target) return emptyArray() // 无解
        // 修改剩余边
        for (edge in edges) {
            if (edge[2] == -1) edge[2] = INF
        }
        return edges
    }

    // return:将 -1 视为 1，并计算从起点到终点的最短路
    private fun dijkstra1(graph:Array<ArrayList<IntArray>>, edges: Array<IntArray>, source :Int, destination:Int) : IntArray {
        val n = graph.size
        val visit = BooleanArray(n)
        val dis = IntArray(n) { INF }
        dis[source] = 0
        while (true) {
            // 寻找最短路长度最短的节点
            var x = -1
            for (i in 0 until n) {
                if (visit[i]) continue
                if (-1 == x || dis[i] < dis[x]) x = i
            }
            if (x == destination) break
            visit[x] = true // 标记
            // 松弛相邻边
            for (to in graph[x]) {
                var w = edges[to[1]][2]
                if (-1 == w) w = 1 // 视为 1
                if (dis[x] + w < dis[to[0]]) dis[to[0]] = dis[x] + w
            }
        }
        return dis
    }

    // 补全
    private fun dijkstra2(graph:Array<ArrayList<IntArray>>, edges: Array<IntArray>, source :Int, destination:Int, delta: Int, originDis:IntArray /* 首轮计算的最短路 */) : IntArray {
        val n = graph.size
        val visit = BooleanArray(n)
        val dis = IntArray(n) { INF }
        dis[source] = 0
        while (true) {
            // 寻找最短路长度最短的节点
            var x = -1
            for (i in 0 until n) {
                if (visit[i]) continue
                if (-1 == x || dis[i] < dis[x]) x = i
            }
            if (x == destination) break
            visit[x] = true // 标记
            // 松弛相邻边
            for (to in graph[x]) {
                var w = edges[to[1]][2]
                if (-1 == w) {
                    // 补全（两次 Dijkstra 只修改这里）
                    w = Math.max(delta - dis[x] + originDis[to[0]], 1) // 题目要求至少修改到 1
                    if (w >= 1) edges[to[1]][2] = w
                }
                if (dis[x] + w < dis[to[0]]) dis[to[0]] = dis[x] + w
            }
        }
        return dis
    }
}

复杂度分析：

• 时间复杂度：$O(n^2)$ 两轮最短路算法；
• 空间复杂度：$O(m)$ 图空间。

往期回顾

• LeetCode 单周赛第 345 场 · 体验一题多解的算法之美
• LeetCode 单周赛第 344 场 · 手写递归函数的通用套路
• LeetCode 双周赛第 104 场 · 流水的动态规划，铁打的结构化思考
• LeetCode 双周赛第 103 场 · 区间求和的树状数组经典应用