git安装和git命令：全局设置用户名邮箱配置

在网上下载并安装git：https://git-scm.com/downloads
在开始菜单里面找到 "Git --> Git Bash",如下

运行Git Bash：

如果出现如下错误：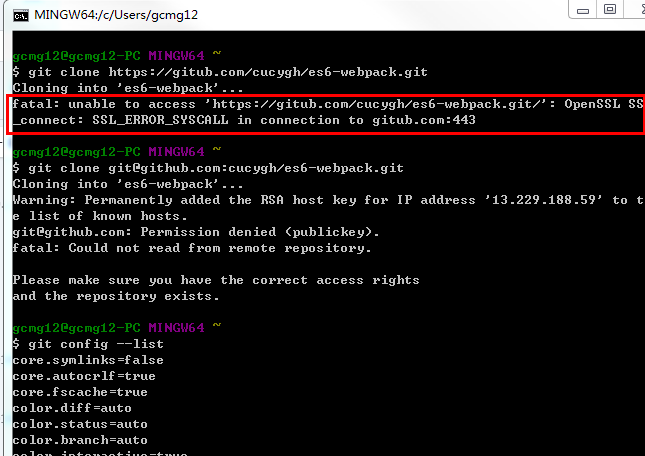

表明此时你未全局配置用户名和邮箱

1、查看git配置信息

git config --list

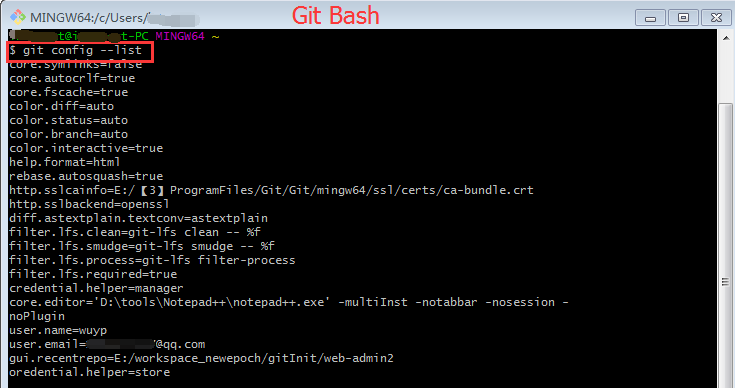
2、查看git用户名

git config user.name

3、查看邮箱配置

git config user.email

4、全局配置用户名

git config --global user.name "nameVal"

5、全局配置邮箱

git config --global user.email "eamil@qq.com"

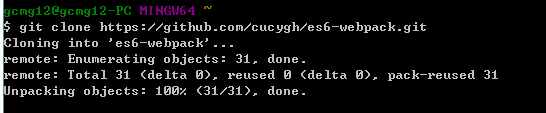
6.重新执行git clone,即可成功