分支界定（ BRANCH-AND-BOUND）

分支定界法（branch and bound）是一种求解整数规划问题的最常用算法。这种方法不但可以求解纯整数规划，还可以求解混合整数规划问题。分支定界法是一种搜索与迭代的方法，选择不同的分支变量和子问题进行分支。

通常，把全部可行解空间反复地分割为越来越小的子集，称为分枝；并且对每个子集内的解集计算一个目标下界（对于最小值问题），这称为定界。在每次分枝后，凡是界限超出已知可行解集目标值的那些子集不再进一步分枝，这样，许多子集可不予考虑，这称剪枝。这就是分枝定界法的主要思路。

分支定界法求解整数规划的一般步骤：

设有最大化的整数规划问题A ，与它相对应的松弛问题为 B。

（1）先不考虑原问题的整数约束，求解相应的松弛问题。用图解法或单纯形法求得最优解，记为 。

（2）若求得的最优解 刚好就是整数解，则该整数解就是原整数规划问题的最优解；否则，对原问题进行分枝寻求整数最优解。

（3）分枝。根据对变量重要性的了解，在最优解中选择一个不符合整数约束条件的x_j ，其值为b_j ，以[b_j]表示小于b_j 的最大整数。构造两个约束条件: x≤ [b_j]和 x≥[b_j]+1分别加入原LP问题形成两个子问题，因为[b_j] 与[b_j]+1之间无整数，故这两个子集内的整数解必定与原可行解集合整数解一致，这一步称为分枝。

（4）定界。首先判断各个子问题是否存在整数解。若存在，找出目标函数值最大对应的整数解，设为Z^*，则A问题的整数解目标函数Z≥Z^*，这就是定界。而且分枝过程中，一旦有某个子问题Z≥Z^*，则令Z^*＝Z。

（5）若存在大于Z^*的子问题则需分枝。第（4）步中若不存在整数解，也需继续分枝寻找整数解，并从目标函数值最大对应的子问题先分枝。

（6）若所有子问题的目标值都小于等于Z^*，则不需继续分枝，Z^*所对应的整数解即为最优解。

分支定界法求背包问题：

问题：一个容量为10的集装箱，有重量分别为4,8,5的货物，如何才能装最多：

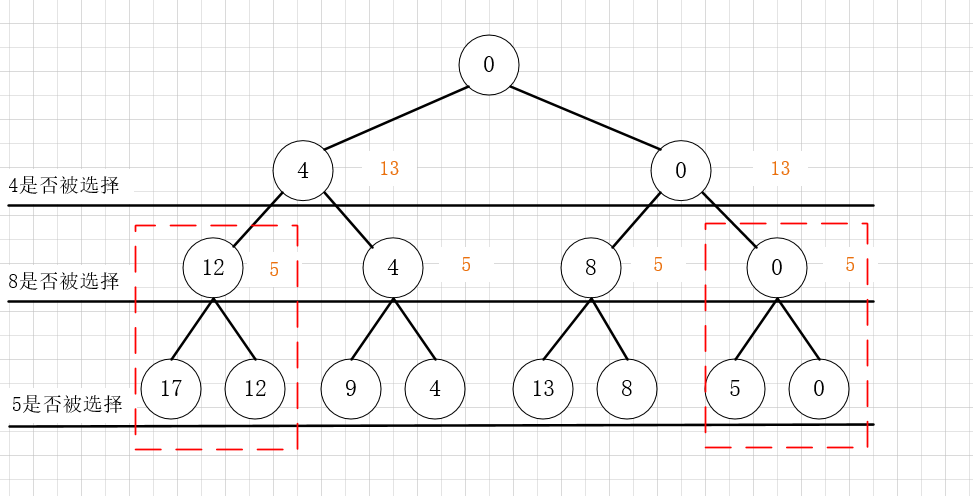
FIFO算法：

1.首先定义best=0

2. 第一层，4被选择，此时的best修改成4，加入到队列中；0<best 计算0节点的最大期望，13>best，加入到队列中。

3.第二层，8被选择，12>10，截枝；4=best，加入到队列中；8>best, 加入到队列，修改best=8，0节点的最大期望小<best，截枝；

4.第三层，修改best即可。

paython代码：

import numpy as np

capacity = 10  # 背包的容量是10
goods = [4, 8, 5]  # 货物重量
best = 0  # 最优重量
expect = sum(goods)  # 期望值

queue = [0]  # 记录每层的节点
layer = 0  # 记录层数

while layer < np.size(goods)-1:
    # 取出该层的所有节点，作为下层的父节点
    expect = expect - goods[layer]  # 修改期望值
    parents = np.array(queue)
    nowParents = parents + goods[layer]
    temp_best = np.max(np.where(nowParents > capacity, 0, nowParents))

    # 更新best
    if best < temp_best:
        best = temp_best

    # 选择候选集， 截枝操作
    nowParents = np.hstack((nowParents, parents))
    temp_queue = []
    for i in nowParents:
        if i + expect > best:
            temp_queue.append(i)
    queue = temp_queue

    layer = layer + 1

# 最后一层，计算最优值
parents = np.array(queue)
nowParents = parents + goods[layer]

nowParents = np.hstack((nowParents, parents))
best = np.max(np.where(nowParents > capacity, 0, nowParents))

print(best)

参考：https://www.cnblogs.com/shixisheng/p/6034779.html

https://www.cnblogs.com/sage-blog/p/3917836.html

https://blog.csdn.net/zack_liu/article/details/78370537