dsu on tree入门

先瞎扯几句

说起来我跟这个算法好像还有很深的渊源呢qwq。当时在学业水平考试的考场上，题目都做完了不会做，于是开始xjb出题。突然我想到这么一个题

看起来好像很可做的样子，然而直到考试完我都只想出来一个莫队的暴力。当时我想知道有没有比莫队更优的做法，和zbq讨论了半天也只能搞出一个$O(nlog^2n)$的平衡树启发式合并

然后！！我就把这题出给校内互测了！！没错，当时是用莫队当的标算！

结果！mjt用一个假的$O(n)$算法艹过去了因为数据特别水

后来我打算把这题出给另一场比赛，结果到了前一天晚上造数据的时候我发现不太对，然后把mjt的算法hack了。

去UOJ群里一问才知道这玩意儿是个dsu on tree的sb题。

当时我就这个表情

自己还是太年轻啊%>_<%

好了好了，来讲算法吧

Dsu on tree

简介

dsu on tree跟dsu(并查集)是没啥关系，可能是借用了一波启发式合并的思想？？

它是用来解决一类树上询问问题，一般这种问题有两个特征

1、只有对子树的询问

2、没有修改

一般这时候就可以强上dsu on tree了

update：可能特征1不会很显然，就是说题目中不一定明确的问你子树$i$的答案，可能是把问题转化后需要算子树$i$的答案

算法流程

考虑暴力怎么写：遍历每个节点—把子树中的所有颜色暴力统计出来更新答案—消除该节点的贡献—继续递归

这肯定是$O(n^2)$的。

dsu on tree巧妙的利用了轻重链剖分的性质，把复杂度降到了$O(nlogn)$

啥啥啥？你不知道啥叫轻重链剖分？

一句话：对于树上的一个点，与其相连的边中，连向的节点子树大小最大的边叫做重边，其他的边叫轻边

dsu on tree的算法流程是这样的：

对于节点$i$：

• 遍历每一个节点
  • 递归解决所有的轻儿子，同时消除递归产生的影响
• 递归重儿子，不消除递归的影响
• 统计所有轻儿子对答案的影响
• 更新该节点的答案
• 删除所有轻儿子对答案的影响

主体框架长这样

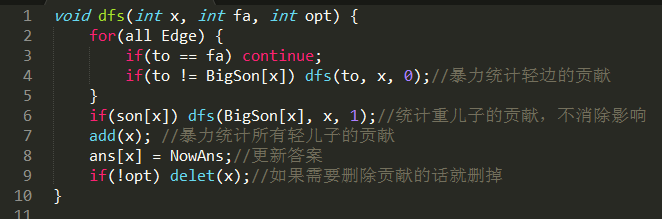
可能你先在会想：为什么都是暴力统计答案？这样复杂度不是$O(n^2)$的么？

那简单的来证一下这东西的复杂度

复杂度

性质：一个节点到根的路径上轻边个数不会超过$logn$条

证明：

设根到该节点有$x$条轻边，该节点的大小为$y$，根据轻重边的定义，轻边所连向的点的大小不会成为该节点总大小的一般。

这样每经过一条轻边，$y$的上限就会$ / 2$，因此$y < \frac{n}{2^x}$

因为$n > 2^x$，所以$x < logn$

然而这条性质并不能解决问题。

我们考虑一个点会被访问多少次

一个点被访问到，只有两种情况

1、在暴力统计轻边的时候访问到。

根据前面的性质，该次数$< logn$

2、通过重边 / 在遍历的时候被访问到

显然只有一次

如果统计一个点的贡献的复杂度为$O(1)$的话，该算法的复杂度为$O(nlogn)$

模板题

cf600E. Lomsat gelral

题意：给出一个树，求出每个节点的子树中出现次数最多的颜色的编号和

dsu on tree的模板题，暴力统计即可

#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int MAXN = 1e5 + ;
inline int read() {
    char c = getchar(); int x = , f = ;
    while(c < '' || c > '') {if(c == '-') f = -; c = getchar();}
    while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
    return x * f;
}
int N, col[MAXN], son[MAXN], siz[MAXN], cnt[MAXN], Mx, Son;
LL sum = , ans[MAXN];
vector<int> v[MAXN];
void dfs(int x, int fa) {
    siz[x] = ;
    for(int i = ; i < v[x].size(); i++) {
        int to = v[x][i];
        if(to == fa) continue;
        dfs(to, x);
        siz[x] += siz[to];
        if(siz[to] > siz[son[x]]) son[x] = to;//轻重链剖分
    }
}
void add(int x, int fa, int val) {
    cnt[col[x]] += val;//这里可能会因题目而异
    if(cnt[col[x]] > Mx) Mx = cnt[col[x]], sum = col[x];
    else if(cnt[col[x]] == Mx) sum += (LL)col[x];
    for(int i = ; i < v[x].size(); i++) {
        int to = v[x][i];
        if(to == fa || to == Son) continue;
        add(to, x, val);
    }
}
void dfs2(int x, int fa, int opt) {
    for(int i = ; i < v[x].size(); i++) {
        int to = v[x][i];
        if(to == fa) continue;
        if(to != son[x]) dfs2(to, x, );//暴力统计轻边的贡献，opt = 0表示递归完成后消除对该点的影响
    }
    if(son[x]) dfs2(son[x], x, ), Son = son[x];//统计重儿子的贡献，不消除影响

    add(x, fa, ); Son = ;//暴力统计所有轻儿子的贡献
    ans[x] = sum;//更新答案
    if(!opt) add(x, fa, -), sum = , Mx = ;//如果需要删除贡献的话就删掉
}
int main() {
    N = read();
    for(int i = ; i <= N; i++) col[i] = read();
    for(int i = ; i <= N - ; i++) {
        int x = read(), y = read();
        v[x].push_back(y); v[y].push_back(x);
    }
    dfs(, );
    dfs2(, , );
    for(int i = ; i <= N; i++) printf("%I64d ", ans[i]);
    return ;
}

一道比较有意思的题

不知道老师从哪儿弄的。。。

我的题解：https://www.cnblogs.com/zwfymqz/p/9687296.html

官方题解：

参考资料

[Codeforces600E]Lomsat gelral（dsu on the tree）

[trick]dsu on tree