LP-KPN
LP-KPN 网络结构

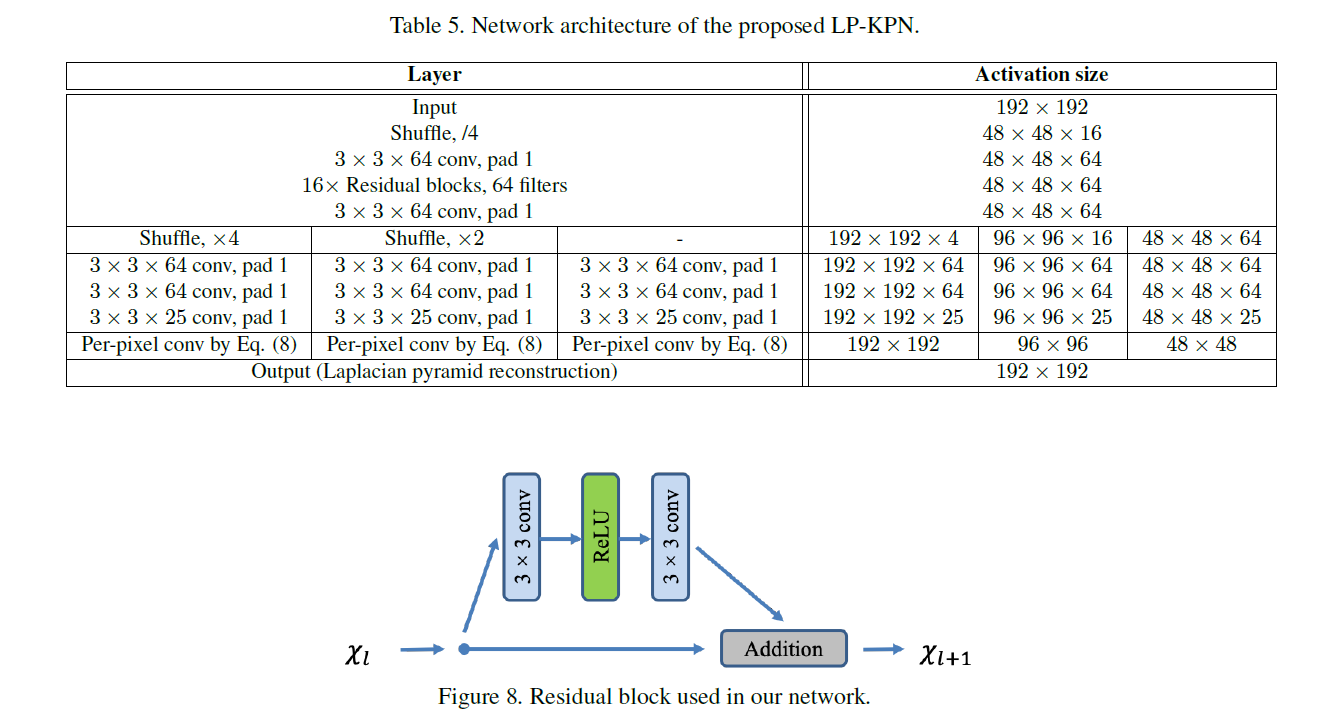
网络解析
1. 网络结构中绿色星星标志 公式。其实就是用预测出来的核在原图片经过Laplacian pyramid decomposes 后的图片上进行卷积运算。所以应该使用padding

2.文章中,该模型是在YCbCr空间上的Y通道实验的
3.最后的Laplacian pyramid restore 过程,应该是使用 Laplacian pyramid unsample (作者没明写,但不是sub-pixel shuffle 网络结构中并未体现)
4.作者提到由于LP的网络结构,使得学习的k*k核等效于4k*4k的核,这减少了参数量
实验参数
1.使用adam训练
2.lr = 1e-4,训练1000K次迭代
3.对于核k的大小,作者在实验中讨论,不一定大的核获取更棒的性能。
实验
实验1:训练数据集的对比,为了展现Real-SR数据集能提高超分辨率的性能,作者使用DIV2K用过BD(bicubic degradation)和MD(multiple degradation)去生成LR,然后用比较流行的模型去训练
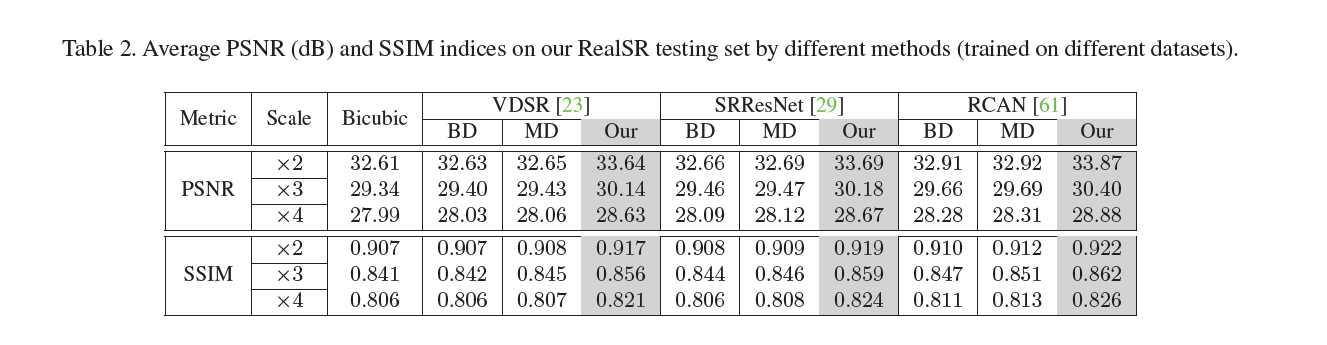
实验2:证明LP-KPN模型性能:通过对比过去的模型,LP-KPN不仅参数量少而且性能也最好,这里也提出核大小为5比KPN核为19更棒,这是由于LP-KPN的结构
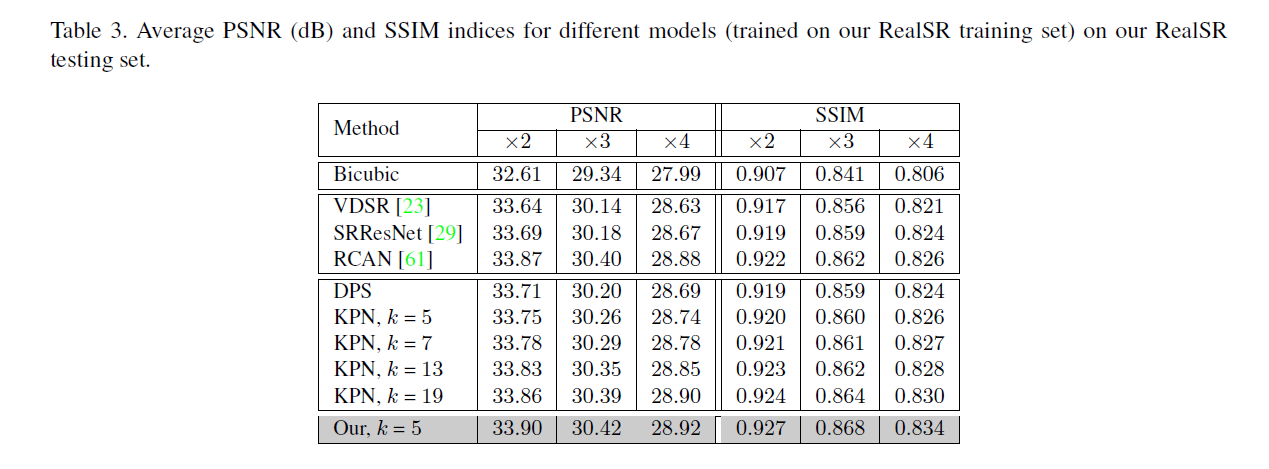
LP-KPN的更多相关文章
- 对偶理论、拉格朗日对偶问题、LP线性规划对偶性质
Lagrange 对偶问题 定义其的对偶问题: Lagrange函数 考虑线性规划问题 若取集合约束D={x|x≥0},则该线性规划问题的Lagrange函数为 线性规划的对偶问题为: 对偶定理原问题 ...
- [原创] 使用LP Wizard 10.5 制作 Allegro PCB封装
本文只讲述使用 Calculator 和 Wizard 功能制作封装,通常学会使用这种方法,通用的标准封装就都可以生成了.下面以一个简单的SOIC-8封装的芯片来说明软件使用方法. 第一步,查找相关d ...
- 压缩感知中的lp球:p范数最优化为什么总会导致一个稀疏的解的原因
转自:彬彬有礼. 压缩感知中的lp球:p范数最优化为什么总会导致一个稀疏的解的原因 http://blog.csdn.net/jbb0523/article/details/40268943 题目: ...
- 关于LP Wizard生成Allegro封装无焊盘的解决方案
最近在学Allegro,安装了软件后看网上说LP Wizard可以一键生成Allegro封装,就想去尝尝鲜.毕竟一直都是手动做封装,没怎么用过向导.但是按照网上教程用LP生成了一个封装,发现打开时没有 ...
- Linux基础命令---lp打印文件
lp lp指令用来打印文件,也可以修改存在的打印任务.使用该指令可以指定打印的页码.副本等. 此命令的适用范围:RedHat.RHEL.Ubuntu.CentOS.Fedora.openSUSE.SU ...
- Lp空间
在数学中,Lp空间是由p次可积函数组成的空间:对应的ℓp空间是由p次可和序列组成的空间.它们有时叫做勒贝格空间,以昂利·勒贝格命名(Dunford & Schwartz 1958,III.3) ...
- 什么是VC、PE、LP、GP?
天使基金主要关注原创项目构思和小型初创项目,投资规模大多在300万元以下:风险投资关注初创时期企业长期投资,规模在1000万元以下:私募股权投资主要关注3年内可以上市的成熟型企业. VC即ventur ...
- LP线性规划求解 之 单纯形 算法
LP线性规划求解 之 单纯形 算法 认识-单纯形 核心: 顶点旋转 随机找到一个初始的基本可行解 不断沿着可行域旋转(pivot) 重复2,直到结果不能改进为止 案例-过程 以上篇的case2的松弛型 ...
- LP线性规划初识
认识LP 线性规划(Linear Programming) 特指目标函数和约束条件皆为线性的最优化问题. 目标函数: 多个变量形成的函数 约束条件: 由多个等式/不等式形成的约束条件 线性规划: 在线 ...
- 线对 Line pairs、LP(分辨率cy/mm)
线对 (Line pairs) 是胶片.镜头等电影摄影领域的专用名词. 每毫米线对一般指分辨率的单位,指仪器在一毫米内能分辨出多少对线. 在一定尺度内的可分辨线对数常被用来衡量仪器的空间分辨能力,能分 ...
随机推荐
- golang str 首字母大写
首字母大写 //如果是小写字母, 则变换为大写字母 func strFirstToUpper(str string) string { if len(str) < 1 { return &quo ...
- 运用了css,js
代码如下: <!DOCTYPE html><html xmlns="http://www.w3.org/1999/html"><head> &l ...
- __x__(28)0907第四天__固定布局
布局 固定布局,需要计算单位 自适应响应布局 固定布局 html代码 <!doctype html> <html> <head> <meta charset ...
- PHP使用 strpos() 注意事项
返回字符出现的第一个位置, 如果字符在被搜索字符串的开头, 则会返回 ‘0’ 因此, 在使用此函数判断 字符串是否包含 某一个字符时 使用: if(strpos('string','str') != ...
- Assembly.LoadFrom加载程序集无法释放资源的解决方案
下面此方法加载程序集会导致程序集一直被占用 Assembly asm = Assembly.LoadFrom(dllPath); 解决方案: //通过此方法读取可以解决dll被占用问题 byte[] ...
- raycast 一小段距离碰撞到的poly
dtNavMeshQuery::raycast(dtPolyRef startRef, const float* startPos, const float* endPos, const dtQuer ...
- vins-mono:雅可比矩阵的推导
imu残差公式 我们计算雅可比采用加扰动形式 以下是位置增量偏差对旋转qbk的雅可比推导 对应的雅可比矩阵的代码 jacobian_pose_i.block<, >(O_P, O_R) = ...
- Python全栈-magedu-2018-笔记4
第三章 - Python 内置数据结构 元组tuple 一个有序的元素组成的集合 使用小括号 ( ) 表示 元组是不可变对象 元组的定义 初始化 定义 tuple() -> empty tupl ...
- C#获取项目程序及运行路径的方
1.asp.net webform用“Request.PhysicalApplicationPath获取站点所在虚拟目录的物理路径,最后包含“\”: 2.c# winform用 A:“Applic ...
- ip通信第七周
局域网的优点:1.具有较高的数据传输率 2.具有较低的误码率 3.具有较低的时延 4.能进行广播 网桥的基本特征:1.网桥在数据链录层上实现局域网互连 2.网桥能够互连两个采用不同数据链路层协议,不同 ...
