机器学习---线性回归（Machine Learning Linear Regression）

线性回归是机器学习中最基础的模型，掌握了线性回归模型，有利于以后更容易地理解其它复杂的模型。

线性回归看似简单，但是其中包含了线性代数，微积分，概率等诸多方面的知识。让我们先从最简单的形式开始。

一元线性回归（Simple Linear Regression）：

假设只有一个自变量x（independent variable，也可称为输入input, 特征feature），其与因变量y（dependent variable，也可称为响应response, 目标target）之间呈线性关系，当然x和y之间不会完全是直线关系，而是会有一些波动（因为在现实中，不一定只有一个自变量x会影响因变量y，可能还会有一些其他影响因素，但是这些因素造成的影响并不大，有些只是偶然出现，这些因素被称之为噪音），因此我们可以将目标方程式写为：

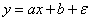
（a表示斜率，b表示截距，表示由噪音造成的误差项，这个误差是无法消除的）

我们根据n个(x-y) pair观测值（observations，或者说是样本samples），想要捕捉x和y之间的关系（不包括噪音）。这样，当出现新的x值时，我们就可以预测出其对应的y值（预测）。不仅如此，我们还能得知特征与目标之间是否存在关联关系，关系强弱如何（推断）。

（读作y-hat）表示对y进行的估计，对于某些观测值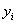，>，而对于另一些观测值，<。

我们假设由噪音造成的误差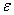独立同分布，且服从平均值为0，方差为σ²的正态分布，那么的方程式就是：

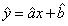
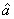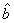（，分别表示对a，b参数的估计）

那么到底怎样的一条直线可以最好地体现出x和y之间的关系呢？

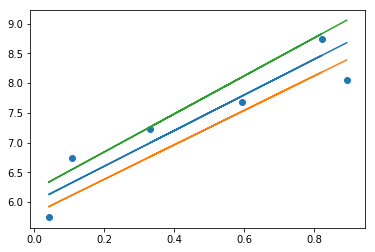
我们肯定希望每个观测值与其估计值之间的误差越小越好。这样，我们可以定义一个损失函数LL：

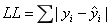
只要每个观测点实际的y值与其在某条直线上对应的y估计值的误差值（绝对值）的总和最小（即所有样本到直线上的欧氏距离之和最小），那么这条直线就是对x和y之间的关系的最好估计。

但是LL并不是一个处处可导的函数，数学上处理起来比较麻烦。因此，我们重新定义了一个数学上容易处理的损失函数L，就是观测值与估计值之间的欧式距离平方和：

只要求出能使L最小的a，b参数估计值，我们就能找到x和y之间最好的对应关系，这被称为最小二乘回归（Least Sqaures Regression）。

统计学上，最小二乘法其实就是使残差平方和（RSS, Residual Sum of Squares）最小化的方法。此外，如果从另外一种角度（使用极大似然估计法）来看，也能达到和最小二乘法同样的结论。

首先，根据中心极限定理（Central Limit Theorem），如果对总体取样足够多，那么每次取样的样本的平均值服从正态分布。据此，我们可以假设由噪音造成的误差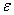独立同分布，且服从平均值为0，方差为σ²的正态分布。而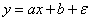，因此，y也独立同分布，且服从平均值为ax+b，方差为σ²的正态分布，其概率密度函数是：，将其写成条件概率表达式就是：。用通俗的话来说：如果对y总体进行n次取样，每次取1个样本，只要取样次数足够多，样本就会呈正态分布，有更多的样本聚集在样本均值附近，且样本均值逐渐逼近总体均值。样本越靠近总体均值肯定越好，因此我们需要使这个概率最大化，可以用极大似然估计法（MLE）来求解，即求出。这样就能找到最佳的参数估计值，此参数估计值能使从模型中抽取的n组样本的概率最大。

由于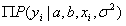有连乘运算，因此我们对似然函数取对数计算，就可以把连乘变成求和：

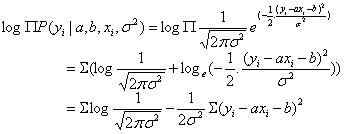
由于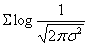和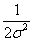均为定值，因此求也就是求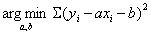，这和上面说的最小二乘法的形式是一样的。

现在，只要对损失函数L分别求偏导，令导数为0，也就是让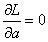和，解出的最值点就是a，b参数的估计值：

可以看出，由于最小二乘回归假设了自变量和因变量之间存在一定的线性关系，因此把问题简化为寻求线性模型的参数值，而不用去估计整个目标函数（这属于parametric method）。这样可能存在的问题就是，如果选择的模型与自变量和因变量之间的真实关系相差太大，那么模型就不能作出较为准确的预测。而non-parametric method可以不用做任何假设，因此它没有上述的问题。但是因为它需要估计整个目标函数，因此需要比parametric method多得多的训练数据。

最小二乘回归只是线性回归模型中的一种，其他的还有k近邻回归（k-nearest neighbors regression），贝叶斯线性回归（Bayesian Linear Regression）等。

k近邻法属于non-parametric method，它把在需要预测的点的x值相邻一段距离内所有对应的y观测值取平均数，作为预测的y值。但是这个方法只适用于特征很少的情况，因为特征越多，维度就越大，数据就越稀疏，这样很难找到足够对应的观测点来计算平均值。

贝叶斯线性回归不同于最小二乘回归，不是去找到模型参数的最佳估计值，而是确定模型参数的分布。具体来说就是在条件概率的基础上加上惩罚项（正则化），这个模型的优点是可以防止过拟合，缺点是计算量很大。

多元线性回归（Multivariate Linear Regression）：

上面说的是最简单的一元线性回归，那么如果特征不止一个呢？这时就要用到多元线性回归，此时目标方程式表示如下：

（x₁~x_p表示p个特征）

参数a，b，特征x以及目标y可以用向量和矩阵的方式表示出来。

首先将特征表示为 n行p+1列的矩阵，每行对应一个样本，每列对应一个特征，外加一维全为1的常数项，记作大写X（因为X是一个matrix）：

（n代表样本数量，p代表特征数量）

然后将目标表示为向量，记作小写y（因为y是一个vector） ：

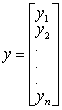
误差项也同理。

学术上通常用θ来表示参数，因此把参数a，b吸收入θ向量，表示为：

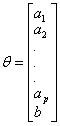
特征和参数之间的乘积可以用矩阵乘法表达式表示出来：

因此，目标方程式最终可以写成：

对y的估计就是：

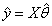
对参数θ的估计就是：

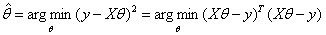
和一元线性回归一样，我们对损失函数求偏导，导数为0的极值点就是对参数θ最好的估计。

具体过程如下，首先展开式子：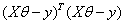

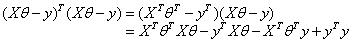
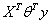得到的结果是  的标量，对于标量 ： ，因此：

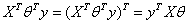
把此结果代入上式：

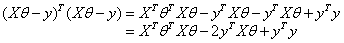
对上式进行求导：

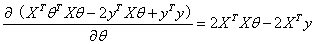
令导数为0（导数为向量形式），这样计算出的θ的最佳估计值为：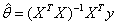

但是这种矩阵解析方程式的方法只在矩阵可逆（满秩）的情况下可用。有时候特征之间相互关联，又或者特征数（矩阵的列）大于样本数（矩阵的行），那么此时矩阵是不满秩的， 上述方程式可解出多个解。即使矩阵是满轶的，但是如果矩阵特别大，那么计算这样一个矩阵的逆是相当耗费时间的。因此，我们需要找到更有效的解决方法。

（注：对于特征数大于样本数的情况，最小二乘回归已不适用，因为在这种情况下会非常容易导致过拟合，解决的办法是进行特征选择）

下面介绍几种常见的求解参数θ估计值的算法，分别是批量梯度下降法，随机梯度下降法和小批量梯度下降法。

在微积分里面，对多元函数的参数求偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度 。例如之前所说的损失函数L的梯度就记作▽L。从几何意义上讲，梯度指向函数增加最快的方向。如果我们需要求解损失函数的最大值，那么就用梯度上升法来迭代；反之，如果我们需要求解损失函数的最小值，就用梯度下降法。

（1）批量梯度下降法（Batch Gradient Descent）

（注：此处还是用矩阵表示法；α表示学习速率，也叫步长）

由于批量梯度下降法每次学习都使用整个训练数据集，因此最后能够保证凸函数收敛于全局极值点，非凸函数可能会收敛于局部极值点，但是缺点是学习时间太长。

（2）随机梯度下降法（Stochastic Gradient Descent）

随机梯度下降法是在批量梯度下降法基础上的优化，一次迭代只用一条随机选取的数据，因此每次学习非常快，但是容易引起振荡。

（3）小批量梯度下降法（Mini-Batch Gradient Descent）

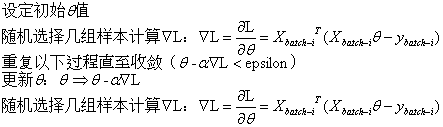
小批量梯度下降法结合了批量梯度下降法和随机梯度下降法的优点，一次迭代多条数据，如果Batch Size选择合理，不仅收敛速度比随机梯度下降法更快，而且在最优解附近的振荡也不会很大。

总结：梯度下降算法针对凸函数是可以收敛到全局最优点的，但是很多模型是非线性结构，一般属于非凸问题，这意味着存在很多局部最优点（鞍点）。采用梯度下降算法可能会陷入局部最优，这是最令人头疼的问题。因此，人们在梯度下降算法的基础上又开发了很多其它优化算法，如：Momentum，AdaGrad、AdaDelta、RMSProp、Adam等。梯度下降算法中一个非常重要的参数是学习速率α，适当的学习速率很重要：学习速率过小时收敛速度慢，而过大时会导致振荡，而且可能会发散（diverge）。理想的梯度下降算法要满足两点：收敛速度快，能全局收敛。

线性回归模型的优点：速度快，容易解释

线性回归模型的缺点：预测效果通常比复杂模型差