LibreOJ 6279 数列分块入门 3(分块+排序)

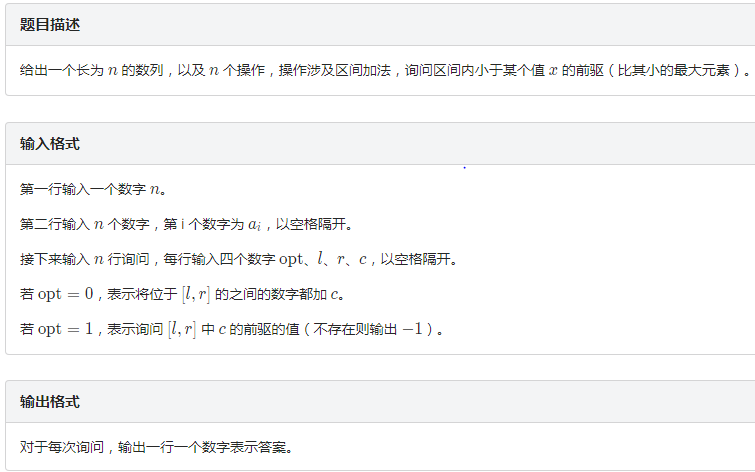
题解:自然是先分一波块,把同一个块中的所有数字压到一个vector中,将每一个vector进行排序.然后对于每一次区间加,不完整的块加好后暴力重构,完整的块直接修改标记.查询时不完整的块暴力找最接近x的解,完整的块用二分查找,其实还可以用set维护,出于对最暴力AC的尊敬,我并没有这么写.照样过了.

代码如下:

#include<cmath>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

int tag[],a[],lump[];
int sz,n;
vector<int> v[];

void reset(int x)
{
    v[x].clear();
    for(int i=(x-)*sz+; i<=min(x*sz,n); i++)
    {
        v[x].push_back(a[i]);
    }
    sort(v[x].begin(),v[x].end());
}

void add(int l,int r,int c)
{
    for(int i=l; i<=min(lump[l]*sz,r); i++)
    {
        a[i]+=c;
    }
    reset(lump[l]);
    if(lump[l]!=lump[r])
    {
        for(int i=(lump[r]-)*sz+; i<=r; i++)
        {
            a[i]+=c;
        }
        reset(lump[r]);
    }
    for(int i=lump[l]+; i<=lump[r]-; i++)
    {
        tag[i]+=c;
    }
}

int query(int l,int r,int x)
{
    int ans=-;
    for(int i=l; i<=min(lump[l]*sz,r); i++)
    {
        if(a[i]+tag[lump[i]]>ans&&x>a[i]+tag[lump[i]])
        {
            ans=a[i]+tag[lump[i]];
        }
    }
    if(lump[l]!=lump[r])
    {
        for(int i=(lump[r]-)*sz+; i<=r; i++)         //!!!
        {
            if(tag[lump[i]]+a[i]>ans&&x>a[i]+tag[lump[i]])
            {
                ans=a[i]+tag[lump[i]];
            }
        }
    }
    for(int i=lump[l]+; i<=lump[r]-; i++)
    {
        int gg=x-tag[i];
        int pos=lower_bound(v[i].begin(),v[i].end(),gg)-v[i].begin();
        if(pos!=)
        {
            int w=v[i][pos-];
            if(w+tag[i]>ans&&w+tag[i]<x)
            {
                ans=w+tag[i];
            }
        }

    }
    return ans;
}

int main()
{
    int opt,l,r,c;
    scanf("%d",&n);
    sz=sqrt(n);
    for(int i=; i<=n; i++)
    {
        lump[i]=(i-)/sz+;
    }
    for(int i=; i<=n; i++)
    {
        scanf("%d",&a[i]);
        v[lump[i]].push_back(a[i]);
    }
    for(int i=; i<=lump[n]; i++)
    {
        sort(v[i].begin(),v[i].end());
    }
    for(int i=; i<=n; i++)
    {
        scanf("%d%d%d%d",&opt,&l,&r,&c);
        if(!opt)
        {
            add(l,r,c);
        }
        else
        {
            printf("%d\n",query(l,r,c));
        }
    }
}