一、打包ipa

个人发布证书和企业发布证书打包 app 大同小异，只是打包时导出选项不同，企业证书打包选择 Save for Enterprise Deployment ，并最终导出 ipa 包。详细步骤这里就不列出了，大家都会。

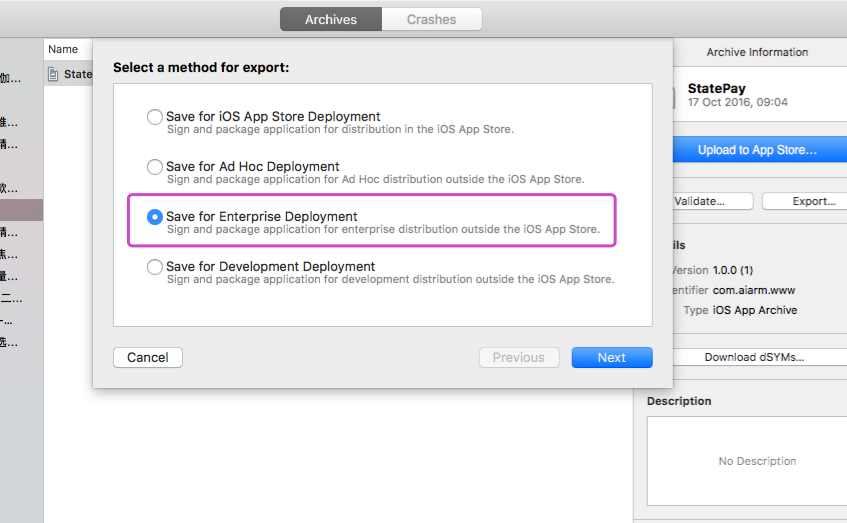
二、配置服务器ssl证书

企业app下载需要我们部署下载环境，其实也就是服务器部署了不是自签名的 ssl 证书，可以用 https 安全链接，就像我的博客这样（https://blog.6ag.cn），推荐我司正在使用的 AlphaSSL 。

这个工作当然是交给后端人员去完成，可参考ssl证书配置笔记：https://blog.6ag.cn/1622.html 。

三、创建plist文件

然后创建 plist 文件并根据规定的格式配置好 app 信息，并上传对应 ipa 包和 AppIcon 图标到对应路径即可。

app.plist图示

app.plist代码

 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
<?xml version="1.0" encoding="UTF-8"?>
<!DOCTYPE plist PUBLIC "-//Apple//DTD PLIST 1.0//EN" "http://www.apple.com/DTDs/PropertyList-1.0.dtd">
<plist version="1.0">
<dict>
    <key>items</key>
    <array>
        <dict>
            <key>assets</key>
            <array>
                <dict>
                    <key>kind</key>
                    <string>software-package</string>
                    <key>url</key>
                    <string>https://api.test.com/app.ipa</string>
                </dict>
                <dict>
                    <key>kind</key>
                    <string>full-size-image</string>
                    <key>needs-shine</key>
                    <true/>
                    <key>url</key>
                    <string>https://api.test.com/icon1.png</string>
                </dict>
                <dict>
                    <key>kind</key>
                    <string>display-image</string>
                    <key>needs-shine</key>
                    <true/>
                    <key>url</key>
                    <string>https://api.test.com/icon2.png</string>
                </dict>
            </array>
            <key>metadata</key>
            <dict>
                <key>bundle-identifier</key>
                <string>com.test.www</string>
                <key>bundle-version</key>
                <string>1.0.0</string>
                <key>kind</key>
                <string>software</string>
                <key>title</key>
                <string>app名称</string>
            </dict>
        </dict>
    </array>
</dict>
</plist>

四、编辑下载网页

一切准备就绪后，我们可以自己写一个漂亮的app下载页面，页面里可以放上我们的Android和iOS app的下载链接，最终用iPhone自带的Safari浏览器打开即可下载安装企业app。

企业iOS app下载链接格式如下：

 
1
<a href="itms-services://?action=download-manifest&url=https://api.test.com/mobile/app.plist">iOS app下载链接</a>
 
 

iOS项目之企业证书打包和发布的更多相关文章

  1. 企业版证书打包APP发布，安装后闪退问题解决。

    企业版证书打包APP发布,安装后闪退问题解决. 我现在就碰到这个问题,只要项目与Swift沾上边的,都会出问题. 如果我们是直接使用开发者证书进行真机调试,那么就不会出现问题,像往常一样好.但如果我们 ...

  2. ios 7.1企业证书无线安装

    ios升级到7.1时,企业证书http服务器发布无线安装不能使用,需要使用https服务器. 测试了几种方式 1.测试时自签名https证书测试无效,提示不能连接到服务器 2.使用dropbox共享连 ...

  3. iOS $299刀企业证书申请的过程以及细节补充(二)

    上篇博客写的过程中,没有图,也没有相应的说明.这次再补充一些信息: 1.从 https://developer.apple.com/ios/enroll/dunsLookupForm.action 申 ...

  4. iOS $299刀企业证书申请的过程以及细节补充

    最近申请了iOS的 299刀企业证书,相关过程有些问题,分享出来,以便后来人参考. 申请的过程我主要参考了别人以前的文章,链接如下: 1.https://developer.apple.com/cn/ ...

  5. 黄聪：iOS $299刀企业证书申请的过程以及细节补充

    最近申请了iOS的 299刀企业证书,相关过程有些问题,分享出来,以便后来人参考.申请的过程我主要参考了别人以前的文章,链接如下: 1.https://developer.apple.com/cn/s ...

  6. 利用 Jenkins 持续集成 iOS 项目，搭建自动化打包环境

    ---恢复内容开始--- jenkins是一个广泛用于持续构建的可视化web工具,持续构建即各种项目的”自动化”编译.打包.分发部署.jenkins可以很好的支持各种语言(比如:Java, c#, P ...

  7. 企业证书发布app到七牛云服务

    ---恢复内容开始--- 最近在做企业证书发布app,从申请企业证书,到测试程序发布到七牛云存储.整了几天终于实现了,整理一下资料. 1.首先,申请企业证书. 到苹果开发网站申请企业证书 https: ...

  8. 【转】手把手教你利用Jenkins持续集成iOS项目

    前言 众所周知,现在App的竞争已经到了用户体验为王,质量为上的白热化阶段.用户们都是很挑剔的.如果一个公司的推广团队好不容易砸了重金推广了一个APP,好不容易有了一些用户,由于一次线上的bug导致一 ...

  9. 手把手教你利用Jenkins持续集成iOS项目

    前言 众所周知,现在App的竞争已经到了用户体验为王,质量为上的白热化阶段.用户们都是很挑剔的.如果一个公司的推广团队好不容易砸了重金推广了一个APP,好不容易有了一些用户,由于一次线上的bug导致一 ...

随机推荐

  1. GDOI2015的某道题目

    分析: 考试的时候由于一些神奇的原因(我就不说是什么了)...没有想$C$题,直接交了个暴力上去... 然后发现暴力的数组开的太大,由于矩阵乘法的需要做$m$次初始化,所以只拿到了10分... 我们一 ...

  2. 【HDU】6146 Pokémon GO

    [题意]一个2*n的网格,再保证步数最少的情况下,求从任意格出发遍历完所有格的方案数,格子八连通.n<=10000,T<=100. [算法]递推,DP [题解]原题链接:蓝桥杯 格子刷油漆 ...

  3. Apache多网站虚拟目录域名

    一台服务器安装了Apache,如何绑定多个域名或网站呢? 最简单高效的方法如下: 1. 先打开Apache的配置文件httpd.conf,在这个文件, 找到这句:“#Include etc/extra ...

  4. Python学习笔记 - day4 - 流程控制

    Python流程控制 Python中的流程控制主要包含两部分:条件判断和循环. Python的缩进和语法 为什么要在这里说缩进和语法,是因为将要学习的条件判断和分支将会涉及到多行代码,在java.c等 ...

  5. C++学习笔记之——内联函数，引用

    本文为原创作品,转载请注明出处 欢迎关注我的博客:http://blog.csdn.net/hit2015spring和http://www.cnblogs.com/xujianqing/ 作者:晨凫 ...

  6. yum软件包安装

    使用yum安装软件 配置yum配置文件 cd /etc/yum.repos.d/ vim rhel7.repo [rhel7-source] name=rhel7-source baseurl=fil ...

  7. kuangbin带你飞 匹配问题 二分匹配 + 二分图多重匹配 + 二分图最大权匹配 + 一般图匹配带花树

    二分匹配:二分图的一些性质 二分图又称作二部图,是图论中的一种特殊模型. 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j ...

  8. Linux驱动 读写文件【转】

    转自:http://blog.csdn.net/h_armony/article/details/7546624 在VFS的支持下,用户态进程读写任何类型的文件系统都可以使用read和write着两个 ...

  9. jQuery九宫格图片拉伸变大代码

    之前看到网上有jQuery九宫格图片拉伸变大代码只可以动六张图片,我改了改做了九张图片都可以做的 图片的布局 成品就是每一个图片都可以动看到大图 css样式 <style> /*九宫格*/ ...

  10. 带你入门代理模式/SpringAop的运行机制

    SpringAop 是spring框架中最重要的一项功能之一,同时也是企业级开发记录事物日志等不可或缺的一部分,如果说你的系统需要记录用户访问接口的操作,那SpringAop是很完美的了,当然,拦截器 ...