「JLOI2015」战争调度

题目

【内存限制：256 MiB】【时间限制：1000 ms】

【标准输入输出】【题目类型：传统】【评测方式：文本比较】

---

题目描述

脸哥最近来到了一个神奇的王国，王国里的公民每个公民有两个下属或者没有下属，这种关系刚好组成一个 $n$ 层的完全二叉树。公民 $i$ 的下属是 $2i$ 和 $2i +1$。最下层的公民即叶子节点的公民是平民，平民没有下属，最上层的是国王，中间是各级贵族。

现在这个王国爆发了战争，国王需要决定每一个平民是去种地以供应粮食还是参加战争，每一个贵族（包括国王自己）是去管理后勤还是领兵打仗。一个平民会对他的所有直系上司有贡献度，若一个平民 $i$ 参加战争，他的某个直系上司 $j$ 领兵打仗，那么这个平民对上司的作战贡献度为 $w_{ij}$。若一个平民 $i$ 种地，他的某个直系上司 $j$ 管理后勤，那么这个平民对上司的后勤贡献度为 $f_{ij}$，若 $i$ 和 $j$ 所参加的事务不同，则没有贡献度。为了战争需要保障后勤，国王还要求不多于 $m$ 个平民参加战争。

国王想要使整个王国所有贵族得到的贡献度最大，并把这件事交给了脸哥。但不幸的是，脸哥还有很多 deadline 没有完成，他只能把这件事又转交给你。你能帮他安排吗？

---

输入格式

第一行两个数 $n,m$。

接下来 $2^{n-1}$ 行，每行 $n-1$ 个数，第 $i$ 行表示编号为 $2^{n-1}-1+ i$ 的平民对其 $n-1$ 个直系上司的作战贡献度，其中第一个数表示对第一级直系上司，即编号为 $\frac{2^{n-1}-1+ i}{2}$ 的贵族的作战贡献度 $w_{ij}$，依次往上。

接下来 $2^{n-1}$ 行，每行 $n-1$ 个数，第 $i$ 行表示编号为 $2^{n-1}-1+ i$ 的平民对其 $n-1$ 个直系上司的后勤贡献度，其中第一个数表示对第一级直系上司，即编号为 $\frac{2^{n-1}-1+ i}{2}$ 的贵族的后勤贡献度 $f_{ij}$ ，依次往上。

---

输出格式

一行一个数表示满足条件的最大贡献值。

---

样例

样例输入

3 4
503 1082
1271 369
303 1135
749 1289
100 54
837 826
947 699
216 389

样例输出

6701

---

数据范围与提示

对于 $100 \%$ 的数据，$2 \leq n \leq 10, \ m \leq 2^{n-1}, \ 0 \leq w_{ij}, f_{ij} \leq 2000$

---

题解

做题经历

做到这道题，已经丧心病狂了。

在扎实的语文功底下 $(90/150 pts)$ ，我只用了 $5 min$ 看懂题目.

然后就开始暴搜......

暴搜思路就是，啥都不管，用 $O(2^{2^N})$ 来枚举一个人到底是去打仗还是后勤，然后计算此时的价值，最后输出最大价值即可。

暴搜思路人人懂，算算时间明年到。

时间复杂度大概$O(2^{2^N})$，你以为这样就完了？不，还有个计算的常数 $2^N$，所以完整复杂度 $O(2^{2^N}×2^N)$真是一个友好的算法

---

正解

基于暴搜，我们可以有一些思考

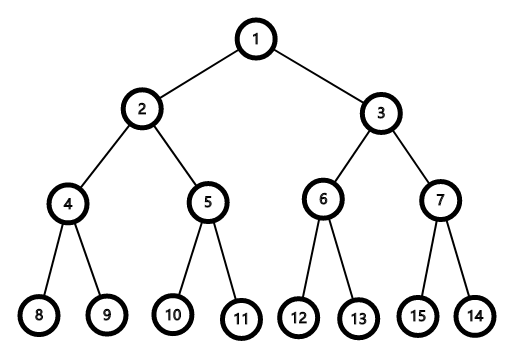
先不考虑 $m$ 的限制。

在这样一棵树里面，平民 $8、9$ 的价值只和他们的所有祖先，也就是 $1、2、4$ 有关

再往上，$4、5$ 的价值只和 $1、2$ 有关

而暴搜复杂度高在何处？

我们做了很多无效的枚举。比如我们要算 $8、9$ 的价值，但是我们却枚举了 $3、5、6、7......$的状态，而这单独对于 $8、9$ 来说，是无效的枚举。

而 $8、9$ 只与他们的祖先有关。

那么我们为什么不考虑一个状态，存下节点编号，以及其祖先状态。

那么一个十分粗糙的状态就出来了：

$dp[s][u]$：节点 $u$ 的祖先状态为 $s$ (二进制串的状压) 时其子树的最大价值。

而这时我们又要考虑 $m$ 对于此题的限制，再加一维：

$dp[s][u][j]$：节点 $u$ 的祖先状态为 $s$ (二进制串的状压) 时，其子树中选了 $j$ 个人去打仗时，这棵子树的最大价值。

那么状转就是：

$dp[s][u][j]=dp[s'][v_1][x]+dp[s'][v_2][y],x+y=j$

这个状转很简单，现在我们来算一下时间复杂度：

首先，对于一个深度为 $k$ 的点

• 其祖先有 $k-1$ 个，那么串 $s$ 有 $2^{k-1}$
• 对于它自己，有两种取值：$1|0$（打仗或者后勤）
• 枚举 $x$ 与 $y$ ，复杂度为$2^{n-k-1}$，有两棵子树，复杂度为${(2^{n-k-1})}^2$

把他们乘起来，时间复杂度$O(2^{k-1}×2×{(2^{n-k-1})}^2)=O(2^{n-k-3})$

但是这个复杂度与 $k$ 有关，不准确，考虑每一层有 $2^{k-1}$ 个节点，那么我们分层计算时间复杂度

每一层的时间复杂度就是 $O(2^{n-k-3}×2^{k-1})=O(2^{2n-4})$

有 $n$ 层，总时间复杂度为 $O(n2^{2n-4})$

时间复杂度有了，似乎不会超时。

开始码代码，但是会发现一个很大的问题：好像这个 $dp$ 数组的空间有点大？

那么我们要省掉一维，哪一维呢?

发现 $s$ 是十分好表示的，我们可以在 $dfs$ 的时候带一个参数 $s$ 来替代掉这一维就可以了。

代码见下：膜拜$trymyedge(lj)$大佬

#include <bits/stdc++.h>
#define mz 1000000007
using namespace std;
 
int n, t;
int c[1005][15][2], siz[15];
int dp[2005][1005];
int add[1005][2005][2];
 
void dfs(int x, int y, int z) {
    if (z == n) {
        dp[x][0] = max(dp[x][0], add[y][x - t][0]);
        dp[x][1] = max(dp[x][1], add[y][x - t][1]);
    } else {
        for (int i = 0; i <= siz[z]; i++) dp[x * 2][i] = dp[x * 2 + 1][i] = 0;
        dfs(x * 2, y, z + 1);
        dfs(x * 2 + 1, y, z + 1);
        for (int i = 0; i <= siz[z]; i++)
            for (int j = 0; j <= siz[z]; j++)
                dp[x][i + j] = max(dp[x][i + j], dp[x * 2][i] + dp[x * 2 + 1][j]);
        for (int i = 0; i <= siz[z]; i++) dp[x * 2][i] = dp[x * 2 + 1][i] = 0;
        dfs(x * 2, y + siz[z], z + 1);
        dfs(x * 2 + 1, y + siz[z], z + 1);
        for (int i = 0; i <= siz[z]; i++)
            for (int j = 0; j <= siz[z]; j++)
                dp[x][i + j] = max(dp[x][i + j], dp[x * 2][i] + dp[x * 2 + 1][j]);
    }
}
 
int main() {
    int m, x, ans = 0;
    scanf("%d%d", &n, &m);
    t = 1 << (n - 1);
    siz[n - 1] = 1;
    for (int i = n - 2; i >= 1; i--) siz[i] = siz[i + 1] * 2;
    for (int i = 0; i < t; i++)
        for (int j = 0; j < n - 1; j++) scanf("%d", &c[i][j][1]);
    for (int i = 0; i < t; i++)
        for (int j = 0; j < n - 1; j++) scanf("%d", &c[i][j][0]);
    for (int i = 0; i < t; i++)
        for (int j = 0; j < t; j++) {
            x = i;
            for (int k = 0; k < n - 1; k++) {
                if (x % 2)
                    add[i][j][1] += c[j][k][1];
                else
                    add[i][j][0] += c[j][k][0];
                x /= 2;
            }
        }
    dfs(1, 0, 1);
    for (int i = 0; i <= m; i++) ans = max(ans, dp[1][i]);
    printf("%d\n", ans);
    return 0;
}