Java实现 LeetCode 429 N叉树的层序遍历

429. N叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。

例如，给定一个 3叉树 :

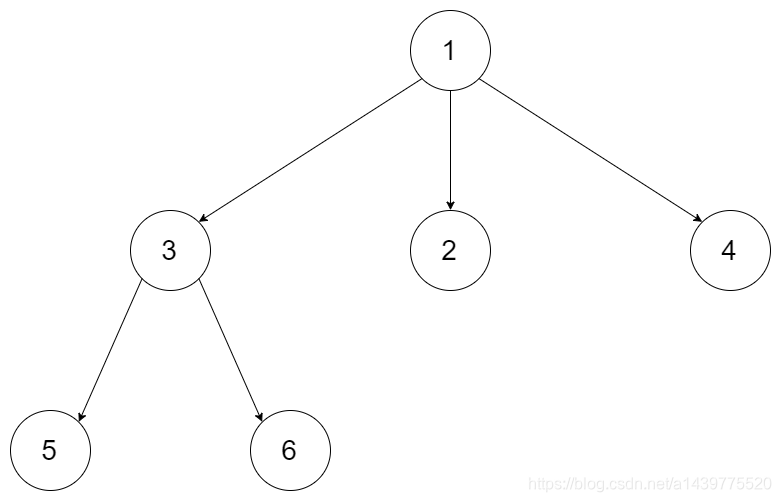
返回其层序遍历:

[
     [1],
     [3,2,4],
     [5,6]
]

说明:

树的深度不会超过 1000。

树的节点总数不会超过 5000。

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
//递归大法

//      public List<List<Integer>> levelOrder(Node root) {
//     List<List<Integer>> res = new ArrayList<>();
//     if (root == null) return res;
//     helper(root, 0, res);
//     return res;
// }

// private void helper(Node root, int depth, List<List<Integer>> res) {
//     if (root == null) return;
//     //判断是否是新的一层
//     if (depth + 1 > res.size()) {
//         res.add(new ArrayList<>());
//     }
//     res.get(depth).add(root.val);

//     //处理子节点
//     for (Node node : root.children) {
//         if (node != null) {
//             helper(node, depth + 1, res);
//         }
//     }
// }

//队列迭代

public List<List<Integer>> levelOrder(Node root) {
    List<List<Integer>> res = new ArrayList<>();
    if (root == null) return res;
    Queue<Node> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        int count = queue.size();
        //外层循环为一层
        List<Integer> list = new ArrayList<>();
        while (count-- > 0) {
            //将当前元素的非空子节点压入栈
            Node cur = queue.poll();
            list.add(cur.val);
            for (Node node : cur.children) {
                if (node != null) {
                    queue.add(node);
                }
            }
        }
        res.add(list);
    }
    return res;
}

}