第1节 IMPALA：2、架构介绍

impala的架构以及查询计划：
impalad :从节点 对应启动一个impala-server的进程 ，主要负责各种查询计划，官方建议与所有的datanode安装在同一台机器上面
impala-statestore : 主节点，状态存储区，主要存储了我们一些查询sql语句的执行情况
impala-catalog:主节点，元数据存储区 建表信息，建库信息，表字段之间的分隔符信息，对应加载hdfs的数据路径信息

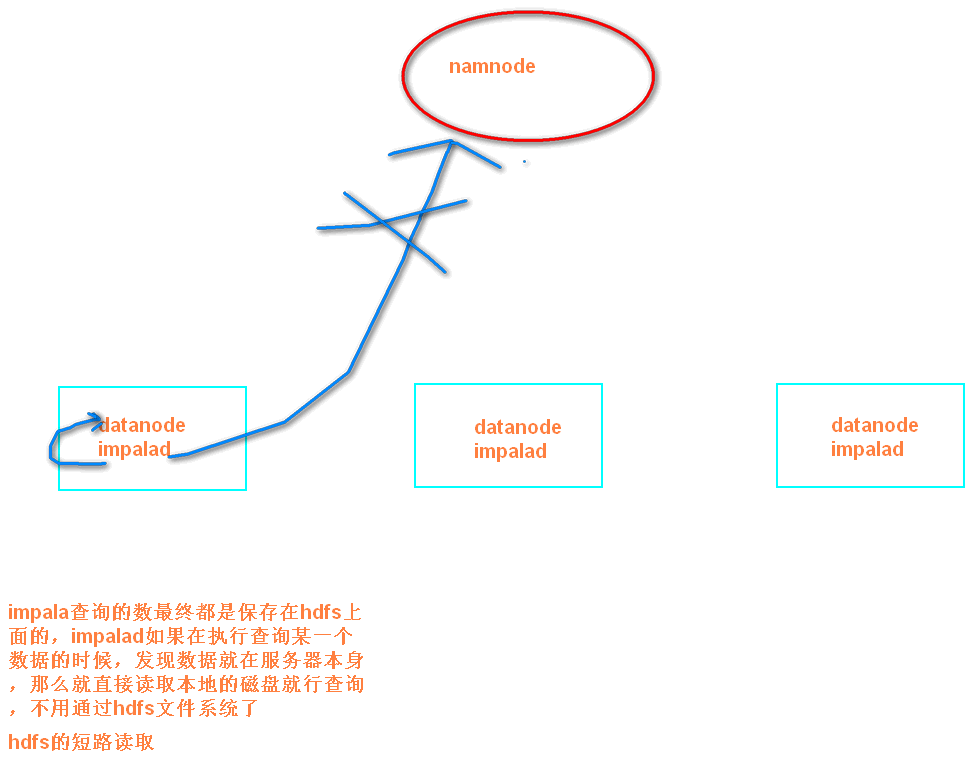
impala的查询过程
第一步：客户端提交查询任务，impala的某一个impalad从节点接收到这个请求
第二步：查询对应的表的元数据信息，我们可以找到hdfs对应的文件路径
第三步：生成单机版的查询计划，决定我们如何去查询数据
第四步：单机版的查询计划，分发给其他所有的impalad的节点，一起执行查询
第五步：查询结果汇总

impala的架构分为两个层次
frontend :使用的是java语言来实现的，前台的一些界面，查询计划的生成等等
backend：C++语言开发的，作为底层的查询的执行来起作用

===============================================

impala的架构以及查询计划

Impala的架构模块：

impala-server  ==>启动的守护进程，执行我们的查询计划 从节点，官方建议与所有的datanode装在一起，可以通过hadoop的短路读取特性实现数据的快速查询

impala-statestore  ==》 状态存储区  主节点

impalas-catalog   ==》元数据管理区  主节点

查询执行

impalad分为frontend和backend两个层次， frondend用java实现（通过JNI嵌入impalad）， 负责查询计划生成， 而backend用C++实现， 负责查询执行。

frontend生成查询计划分为两个阶段：

（1）生成单机查询计划，单机执行计划与关系数据库执行计划相同，所用查询优化方法也类似。

（2）生成分布式查询计划。 根据单机执行计划， 生成真正可执行的分布式执行计划，降低数据移动， 尽量把数据和计算放在一起。

上图是SQL查询例子， 该SQL的目标是在三表join的基础上算聚集， 并按照聚集列排序取topN。

impala的查询优化器支持代价模型（了解）： 利用表和分区的cardinality，每列的distinct值个数等统计数据， impala可估算执行计划代价， 并生成较优的执行计划。 上图左边是frontend查询优化器生成的单机查询计划， 与传统关系数据库不同， 单机查询计划不能直接执行， 必须转换成如图右半部分所示的分布式查询计划。 该分布式查询计划共分成6个segment（图中彩色无边框圆角矩形）， 每个segment是可以被单台服务器独立执行的计划子树。

impala支持两种分布式join方式， 表广播和哈希重分布：

表广播方式保持一个表的数据不动， 将另一个表广播到所有相关节点（图中t3）；

哈希重分布的原理是根据join字段哈希值重新分布两张表数据(譬如图中t1和t2）。

分布式计划中的聚集函数分拆为两个阶段执行。第一步针对本地数据进行分组聚合（Pre-AGG）以降低数据量， 并进行数据重分步， 第二步， 进一步汇总之前的聚集结果（mergeAgg）计算出最终结果。

与聚集函数类似， topN也是分为两个阶段执行， （1）本地排序取topN，以降低数据量； （2） merge sort得到最终topN结果。

Backend从frontend接收plan segment并执行， 执行性能非常关键，impala采取的查询性能优化措施有向量执行。 一次getNext处理一批记录， 多个操作符可以做pipeline。LLVM编译执行， CPU密集型查询效率提升5倍以上。IO本地化。 利用HDFS short-circuit local read功能，实现本地文件读取Parquet列存，相比其他格式性能最高提升5倍。