深度优先搜索理论基础与实践（java）

概论

深度优先搜索属于图算法的一种，是一个针对图和树的遍历算法，英文缩写为 DFS 即 Depth First Search。深度优先搜索是图论中的经典算法，利用深度优先搜索算法可以产生目标图的相应拓扑排序表，利用拓扑排序表可以方便的解决很多相关的图论问题，如最大路径问题等等。一般用堆数据结构来辅助实现 DFS 算法。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。

基本步奏

（1）对于下面的树而言，DFS 方法首先从根节点1开始，其搜索节点顺序是 1,2,3,4,5,6,7,8（假定左分枝和右分枝中优先选择左分枝）。

 

 

（2）从 stack 中访问栈顶的点；

（3）找出与此点邻接的且尚未遍历的点，进行标记，然后放入 stack 中，依次进行；

 

（4）如果此点没有尚未遍历的邻接点，则将此点从 stack 中弹出，再按照（3）依次进行；

（5） 由于与节点 5 相连的的节点都被访问过了，于是5被弹出，查找与 4 相邻但没有被访问过的节点：

（6）直到遍历完整个树，stack 里的元素都将弹出，最后栈为空，DFS 遍历完成。

 

（7）

针对上面的过程，可以用代码表示如下：

    // 用于记录某个节点是否访问过
　　 private Map<String, Boolean> status = new HashMap<String, Boolean>();
　　// 用于保存访问过程中的节点
    private Stack<String> stack = new Stack<String>();
　　// 入口，这里选择 1 为入口
    public void DFSSearch(String startPoint) {
        stack.push(startPoint);
        status.put(startPoint, true);
        dfsLoop();
    }
    private void dfsLoop() {
　　　　　// 到达终点，结束循环
        if(stack.empty()){
            return;
        }
        // 查看栈顶元素，但并不出栈
        String stackTopPoint = stack.peek();
        // 找出与此点邻接的且尚未遍历的点，进行标记，然后全部放入list中。
        List<String> neighborPoints = graph.get(stackTopPoint);
        for (String point : neighborPoints) {
            if (!status.getOrDefault(point, false)) { //未被遍历
                stack.push(point);
　　　　　　　　　 // 加上已访问标记
                status.put(point, true);
                dfsLoop();
            }
        }
　　　　 // 如果邻接点都被访问了，那么就弹出，相当于是恢复操作，也就是在递归后面做的。
        String popPoint =  stack.pop();
        System.out.println(popPoint);
    }

通过上面的示例，基本了解 dfs 使用。

通用框架

其一般框架原理如下：

void dfs()
{
    if(到达终点状态)
    {
        ... //根据题意添加
        return;
    }
    if(越界或不合法状态) return;
    if(特殊状态) // 剪枝
         return;
    for(扩展方式)
    {
        if(扩张方式所到达状态合法)
        {
            修改操作； // 根据题意添加
            标记；
            dfs();
            (还原标记);
            //是否加上还原标记根据题意
            //如果加上还原标记就是回溯法
        }
    }
}

通过这个 dfs 框架可以看出该方法主要有以下几个规律：

1. 访问路径的确定。根据不同的题目思考怎么才算是一条访问路径，如何去实现遍历。

2. 起点条件。从哪个点开始访问？是否每个点都需要当作起点？第一次 dfs 调用至关重要。

3. 递归参数。也就是 dfs 递归怎么在上一个节点的基础上继续递归，实现递归依赖什么参数？需要知道一条路径上各个节点之间的关系，当前访问节点。

4. 终结条件。访问的终结条件是什么？比如到达边界点，所有点已经都访问过了。终结条件需要在下一次递归前进行判断。

5. 访问标志。当一条路走不通的时候，会返回上一个节点，尝试另一个节点。为了避免重复访问，需要对已经访问过的节点加上标记，避免重复访问。

6. 剪枝。属于算法优化。比如已经知道沿着当前路径再走下去也不会满足条件的时候，提前终止递归。

下面将结合几道算法题来加深对深度优先搜索算法的理解。

1、全排列

问题：给定大于0的数字n，输出数字 1 ~ n 之间的全排列。

对于这道题目，有些人可能会好奇为啥这到题目可以使用 dfs 算法。对于全排列，其实可以通过树的形式来进行理解：

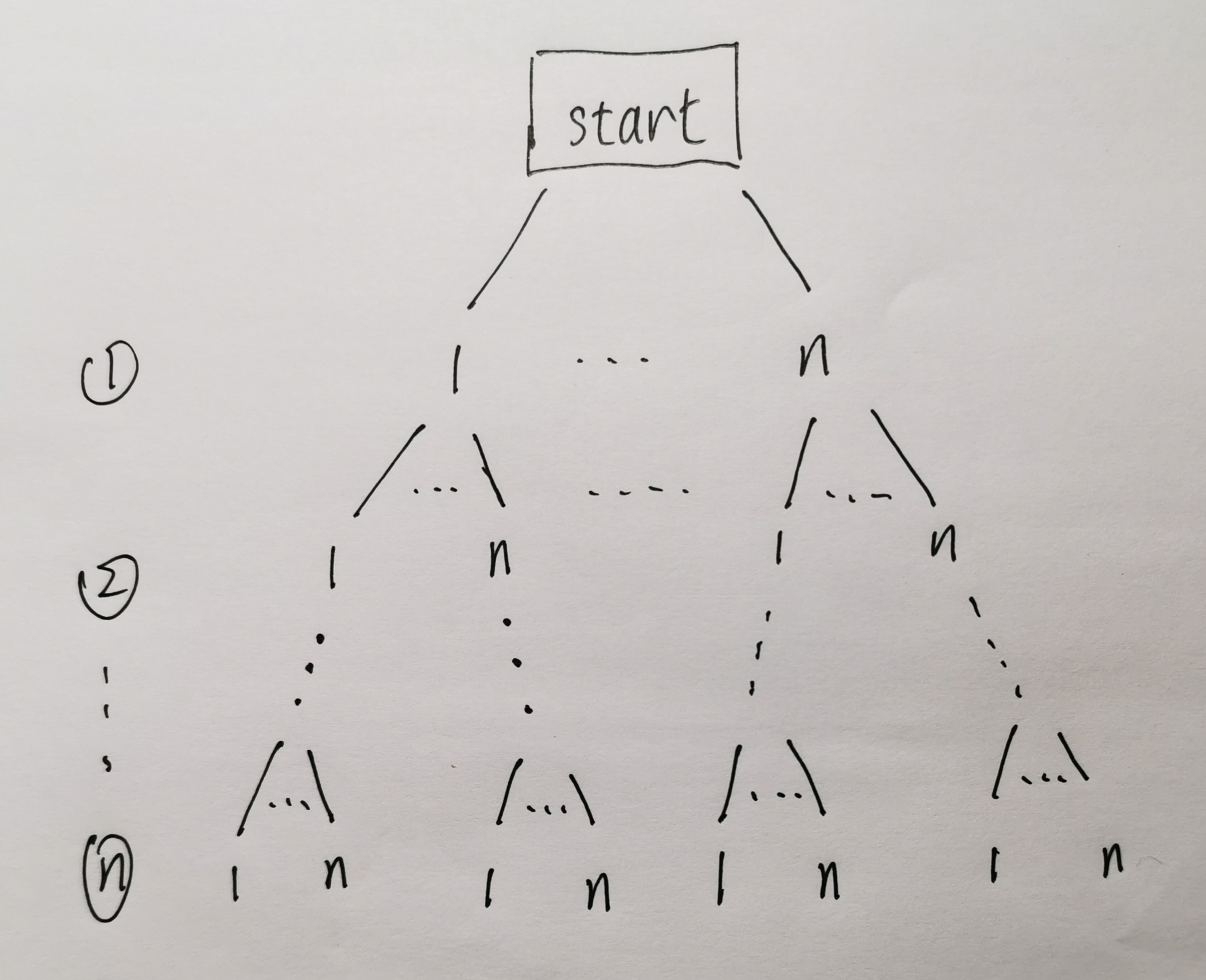
可以发现就是一个 n 叉树，总共是 n 层，下面采用前面总结的规律来看看算法实现原理：

1. 访问路径：从起始位置到叶节点就是一个排列，也就是一条路径

2. 起点条件：start 下面有 n 个节点，每个点都可以被当作起始点，说明需要采用 for 循环方式，。

3. 递归参数：当前访问的节点位置，定位下一个递归节点。需要一个变量记录数字的排列，需要输出。节点总数 n，便于知道何时递归结束。

4. 终结条件：递归访问到节点数到达 n 层的时候停止递归。

5. 访问标志：不需要，可重复访问；

6. 剪枝：不需要，没有其他需要提前终止递归的条件。

下面就是算法实现：

     // 调用入口,起始点
　　　dfs(total, 0, "");
　　　// 递归参数：tatal 表示数字n, index 当前访问节点，s 记录排列方式
     public  void dfs(int total, int index, String s) {
　　　　　// 终结条件
        if (index == total) {
             System.out.println(s);
             return;
        }
　　　　　// 对于每个节点，当前有 total 种选择
        for (int i= 1;i<=total;i++) {
            dfs(total, index+1, s+i);
        }
    }

可以发现，代码还是很简单的。

---

695. 岛屿的最大面积

给定一个包含了一些 0 和 1 的非空二维数组 grid 。

一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)

示例 1:

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

示例 2:

[[0,0,0,0,0,0,0,0]]

对于上面这个给定的矩阵, 返回 0。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

---

对于这道题目还是采用之前的分析方式：

1. 访问路径：节点中相邻的1构成一条路径。0 直接无视。

2. 起点条件：二维数组的每个点都可以当作起点。所以两个 for 循环来进行调用。

3. 递归参数：当前访问的节点位置（x，y），二维数组表，从表中查找下一个节点

4. 终结条件：到达二维数组的边界，节点为0

5. 访问标志：需要，不可重复访问；可以将访问过的节点置为0，避免再次访问，重复计算。

6. 剪枝：只有在节点等于1的时候，才调用dfs。这样可以减少调用次数。

题目解答如下：

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        if (grid == null || grid.length <1 || grid[0].length<1) {
            return 0;
        }
        int rx = grid.length;
        int cy = grid[0].length;
        int max = 0;
        for (int x =0; x< rx; x++) {
            for (int y= 0;y<cy; y++) {
                if (grid[x][y]==1) { //只有节点等于1才调用，这里就可以算作是剪枝，算法的优化
                   int num = dfs(grid,x,y);
                   max = Math.max(max, num);
                }
            }
        }
        return max;

    }
　　 // 递归参数：节点位置x,y, 二维数组
    private int  dfs (int[][] grid, int x, int y){
        int rx = grid.length;
        int cy = grid[0].length;
　　　　　// 边界条件，节点为0
        if (x >= rx || x < 0 || y>=cy || y<0 || grid[x][y]==0 ) {
            return 0;
        }
　　　　　// 直接修改原数组来标记已访问
        grid[x][y]=0;
　　　　　// 每次递归就表示面积多了一块
        int num = 1;
　　　　 // 每个节点有四种不同的选择方向
        num += dfs(grid, x-1, y);
        num += dfs(grid, x, y-1);
        num += dfs(grid, x+1, y);
        num += dfs(grid, x, y+1);
        return num;
    }
}

200. 岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1:

// 输入:
11110
11010
11000
00000
// 输出: 1

示例 2:

// 输入:
11000
11000
00100
00011
// 输出: 3

解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。

---

可以发现，这道题目与前面的题目很类似，关于 dfs 规则这里就不在分析了，留给大家自己去分析。

题目解答如下：

class Solution {
    public int numIslands(char[][] grid) {
        if (grid == null || grid.length < 1 || grid[0].length<1) {
            return 0;
        }
        int num = 0;
        int rx = grid.length;
        int cy = grid[0].length;
　　　　　// 起始点
        for (int x =0;x<rx;x++) {
            for (int y =0;y<cy;y++) {
　　　　　　　　　 // 题目要求，'0'不符合路径条件
                if (grid[x][y]=='1') {
                    dfs(grid,x,y);
                    num++;
                }
            }
        }
        return num;

    }
　　 // 递归条件
    private void dfs(char[][] grid, int x, int y) {
        int rx = grid.length;
        int cy = grid[0].length;
　　　　　// 终结条件
        if (x<0 || x>=rx || y<0 || y>= cy || grid[x][y] == '0') {
            return;
        }
　　　　　// 访问方向实质是由访问路径来决定的，就是你得想清楚怎么才算一条路径
        grid[x][y]='0';
        dfs(grid,x-1,y);
        dfs(grid,x,y-1);
        dfs(grid,x+1,y);
        dfs(grid,x,y+1);
        return ;
    }
}

到这里，深度优先搜索的理论和实践就讲完了，相信看到这里的小伙伴应该也掌握了其算法的原理，以及如何去书写。

参考文章

基本算法——深度优先搜索（DFS）和广度优先搜索（BFS）