JMeter学习笔记--关联
1、什么是关联?
本次请求需要的数据,需要上一步的请求返回给提供的过程。
2、JMeter关联中常用的两种方式
- 正则表达式提取器
- 正则表达式提取器用于对页面任何文本的提取,提取的内容是根据正则表达式在页面内容中进行文本匹配
- XPath Extractor
- 可以提取返回页面任意元素的任意属性
3、实例演示
倒着描述,可能会更容易理解
1)“执行注册”http请求有一参数是由“获取formhash随机值”http请求提供的
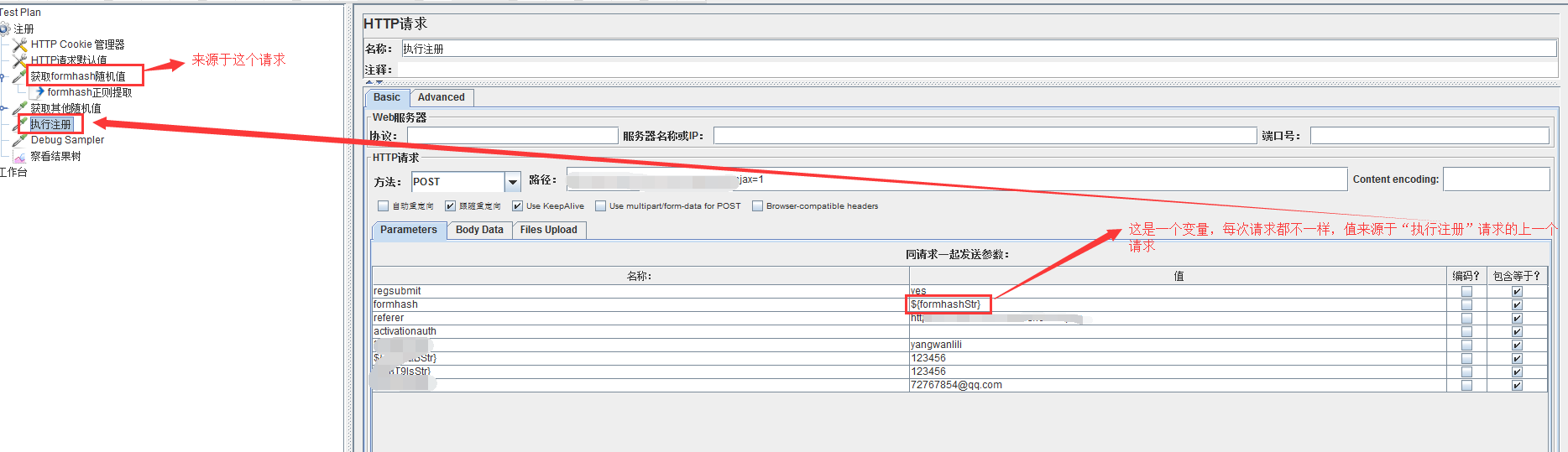
2)"获取formhash随机值"http请求如下图

用fiddler抓包查看该参数在页面的位置及展现形式

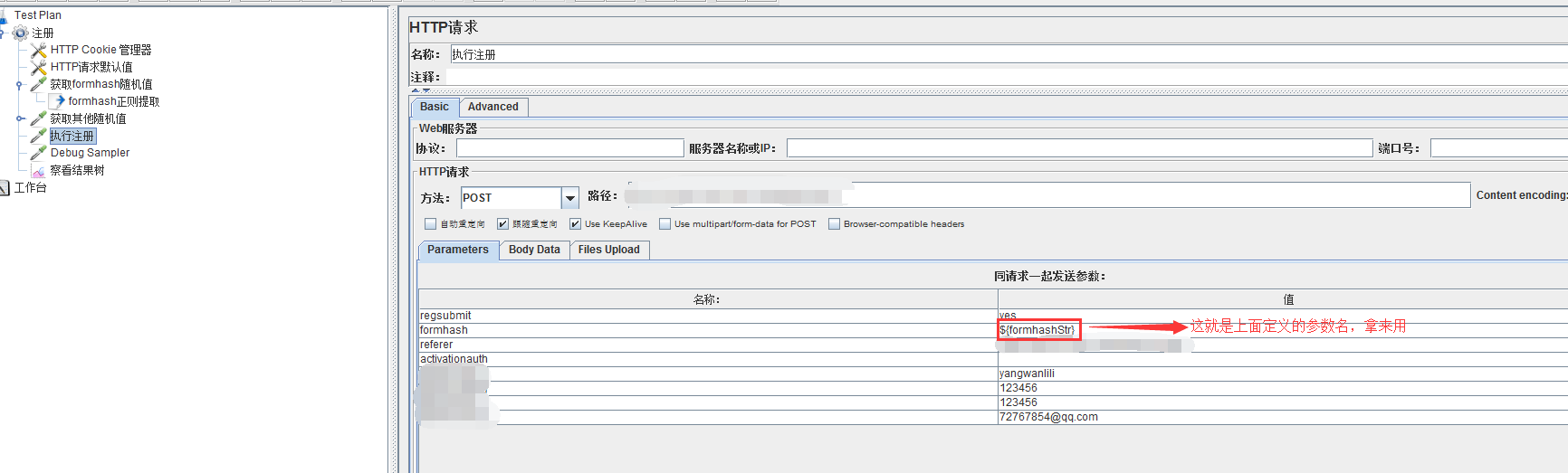
3)用正则表达式提取器
http请求如下图所示添加正则表达式提取器


值已经提取出来,回到第一步开始应用
debug查看一下是否取到值
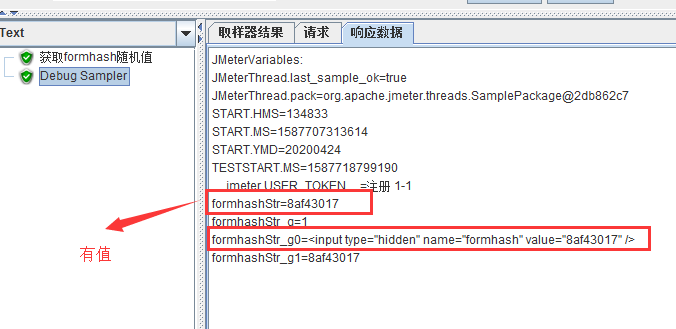
有值,关联成功。
JMeter学习笔记--关联的更多相关文章
- JMeter学习笔记01-安装环境
记录关于JMeter学习的内容.方便复习. 1)JMeter运行环境 因为JMeter是用纯java写的.所以运行的时候需要java的运行环境. 去java官网下载,点免费下载或所有Java下载都行, ...
- JMeter学习笔记(五)-总结
本周主要学习了JMeter如下几方面内容: (1)Bdboy录制方式: (2)JMeter的代理录制方式: (3)关联,在关联时我们要找到哪些内容是要关联的,这个主要通过分析哪些内容是由服务器返回的, ...
- JMeter 学习笔记从不懂慢慢提升(01)
开源已经成为一个趋势,虽然说做测试是一个低端的行业,但是我们也应该在这个低端的行业慢慢提升自己,让自己到达理想的高度. 以前说如果你会使用loadrunner可能别人就会觉得你有一定的水平那么就会拿高 ...
- JMeter学习笔记--JMeter常用测试元件
JMeter测试计划有一个被称为“函数测试模式”的选项,如果被选择,它会使Jmeter记录来自服务器返回的每个取样的数据.如果你在测试监听器中选择一个文件,这个数据将被写入文件.如果你尝试一个较小的测 ...
- JMeter学习笔记(二) 一些实际应用的基础操作
我在CSDN上面找到一位大师整理的jmeter性能测试基础,分享到这里继续学习 https://blog.csdn.net/u011541946/article/category/6893578/1
- JMeter学习笔记(一) 工具的安装和基本介绍
因为网上的资料比较多,就不多描述了,在此引用了其他大神的文档,用于学习 这个文档中有比较详细的jmeter工具介绍: https://wenku.baidu.com/view/64f3a5f75901 ...
- JMeter学习笔记(三)
D. User Defined Variables:用户自定义的变量,在此我们可以定义后面原件需要引用的变量并对其进行赋值.jsessionid一般是服务器返回的,每个用户返回的都不一样,所以在此不应 ...
- jmeter学习笔记-----第一天
环境简介:apache-jmeter-3.3 win10系统 一.Jmeter录制操作步骤: 1.工作台---添加HTTP代理服务器: 2.为自己笔记本的浏览器设置相同代理: 3.测试计划下-s ...
- Jmeter学习笔记(十九)——后置处理器之正则表达式的使用
一.正则表达式提取器的作用 允许用户从服务器的响应中通过使用perl的正则表达式提取值.作为一个后置处理器,该元素会作用在指定范围的取样器,应用正则表达式,提取所需要的值,生成模板字符串,并将结果存储 ...
随机推荐
- javascript 字符串反转 strip_tags 字符串常用的自定义函数,加载css etc.
字符串反转 String.prototype.reverse = function() { var a = this.split(''); for (var i = 0, j = a.length-1 ...
- layui 添加复选框checkbox后,无法正确显示及点击的方法
layui 添加复选框checkbox后,无法正确显示方式,这个是由于html里的样式添加 layui-form后,没有加载 form插件 ,具体如下: <body style="ba ...
- Linux python 虚拟环境管理
直接复制的内容: 原著:https://www.cnblogs.com/q767498226/p/11099884.html 报错解决:https://blog.csdn.net/weixin_467 ...
- YbtOJ#526-折纸游戏【二分,hash】
正题 题目链接:https://www.ybtoj.com.cn/problem/526 题目大意 一个\(n\times m\)的网格上有字母,你每次可以沿平行坐标轴对折网格,要求对折的对应位置字母 ...
- ❤️【Python从入门到精通】(二十六)用Python的PIL库(Pillow)处理图像真的得心应手❤️
您好,我是码农飞哥,感谢您阅读本文,欢迎一键三连哦. 本篇重点介绍Python处理图像的标准库PIL库,处理图像真的的很方便. 干货满满,建议收藏,需要用到时常看看. 小伙伴们如有问题及需要,欢迎踊跃 ...
- html2canvas 无法渲染网络图片及本地 解决方案
使用html2canvas插件可以无法渲染图片的情况 在使用html2canvas的时候.如果元素中还包含网络图片.那么有很大的几率渲染不出来.即时把html2canvas的允许跨域打开也无济于事.这 ...
- [源码解析] PyTorch 流水线并行实现 (5)--计算依赖
[源码解析] PyTorch 流水线并行实现 (5)--计算依赖 目录 [源码解析] PyTorch 流水线并行实现 (5)--计算依赖 0x00 摘要 0x01 前文回顾 0x02 计算依赖 0x0 ...
- Django对表单进行增删改查
查 首先在url中写好路径 其次在后面参数的views里写函数类xxxxxxx的基本逻辑 定义一个函数xxxxxxx,继承request,注意这个request对数据库操作结果都会存放在request ...
- ToString()字符串转换你用正确了吗?
前言 在开发中,ToString()这个方法太方便了,以致于误解大家转换时都是直接Object.ToString()直接转换, 其实不然, 一般都是转之前先判断是否为null后再进行转换,否则会直接报 ...
- 使用 z3 进行逆向 解密字符串
在逆向过程中,我们知道了一个结果值,和一段计算代码.这个时候我们需要知道计算前的值是什么:需要用到 z3 模块来进行解题 z3项目地址 Java代码如下: private String b(Strin ...
