PCA基本原理
降维问题的优化目标:将一组N维向量降维k维(K大于0,小于N),其目标是选择K个单位(模为1)正交基,使得原始数据变换到这组基上后,
选择然数据点之间方差最大的方向作为坐标轴
各字段两两间协方差为0,而字段的方差则尽可能大
为什么协方差为0的时候,连个点的关系最小?
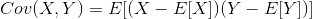

 协方差计算公式
协方差计算公式
由于上面我们已经将每个字段的均值都化0 了,因此方差可以直接用每个元素的平方和除以元素个数表示

为了让协方差都等于0,需要对协方差矩阵进行矩阵对角化,把协方差矩阵变成对角矩阵
协方差矩阵原本就是对称矩阵
而一个n行n列的对称矩阵一定能找到n个单位正交特征向量,用这n个单位特征向量对协方差矩阵对角化
得到特征值

https://www.cnblogs.com/wj-1314/p/8032780.html
PCA基本原理的更多相关文章
- 【机器学习基础】无监督学习(1)——PCA
前面对半监督学习部分作了简单的介绍,这里开始了解有关无监督学习的部分,无监督学习内容稍微较多,本节主要介绍无监督学习中的PCA降维的基本原理和实现. PCA 0.无监督学习简介 相较于有监督学习和半监 ...
- 跟我学算法-PCA(降维)基本原理推导
Pca首先 1.对数据进行去均值 2.构造一个基本的协方差矩阵1/m(X)*X^T 3对协方差矩阵进行变化,得到对角化矩阵,即对角化上有数值,其他位置上的数为0(协方差为0),即求特征值和特征向量的过 ...
- PCA and kmeans MATLAB实现
MATLAB基础知识 l Imread: 读取图片信息: l axis:轴缩放:axis([xmin xmax ymin ymax zmin zmax cmin cmax]) 设置 x.y 和 ...
- Kernel Methods (5) Kernel PCA
先看一眼PCA与KPCA的可视化区别: 在PCA算法是怎么跟协方差矩阵/特征值/特征向量勾搭起来的?里已经推导过PCA算法的小半部分原理. 本文假设你已经知道了PCA算法的基本原理和步骤. 从原始输入 ...
- C8051 PCA实现红外遥控接收
这里使用的处理器是C8051F005.红外接收头接处理器引脚,中断方式接收按键数据. 一 PCA介绍 1.1 PCA 可编程计数器阵列(PCA)提供增强的定时器功能,与标准8051计数器/定时器相比, ...
- 机器学习实战 - 读书笔记(13) - 利用PCA来简化数据
前言 最近在看Peter Harrington写的"机器学习实战",这是我的学习心得,这次是第13章 - 利用PCA来简化数据. 这里介绍,机器学习中的降维技术,可简化样品数据. ...
- matlab pca基础知识
PCA的一些基本资料 最近因为最人脸表情识别,提取的gabor特征太多了,所以需要用PCA进行对提取的特征进行降维. 本来最早的时候我没有打算对提取的gabor特征进行降维,但是如果一个图像时64*6 ...
- OpenCV学习(35) OpenCV中的PCA算法
PCA算法的基本原理可以参考:http://www.cnblogs.com/mikewolf2002/p/3429711.html 对一副宽p.高q的二维灰度图,要完整表示该图像,需要m = ...
- 机器学习:PCA(高维数据映射为低维数据 封装&调用)
一.基础理解 1) PCA 降维的基本原理 寻找另外一个坐标系,新坐标系中的坐标轴以此表示原来样本的重要程度,也就是主成分:取出前 k 个主成分,将数据映射到这 k 个坐标轴上,获得一个低维的数据集. ...
随机推荐
- 开源搜索引擎排名第一,Elasticsearch是如何做到的?
一.引言 随着移动互联网.物联网.云计算等信息技术蓬勃发展,数据量呈爆炸式增长.如今我们可以轻易得从海量数据里找到想要的信息,离不开搜索引擎技术的帮助. 作为开源搜索引擎领域排名第一的 Elast ...
- python练习 - 系统基本信息获取(sys标准库)+ 二维数据表格输出(tabulate库)
系统基本信息获取 描述 获取系统的递归深度.当前执行文件路径.系统最大UNICODE编码值等3个信息,并打印输出. ...
- e3mall商城的归纳总结2之认识dubbo、zookeeper
由于本项目用的是soa架构,因此必须需要两个系统之间进行通信,目前的解决办法有三种(本人认为) Webservice:效率不高基于soap协议.项目中不推荐使用. 使用restful形式的服务:htt ...
- Unity WebGL WebSocket
在线示例 http://39.105.150.229/UnityWebSocket/ 快速开始 安装环境 Unity 2018.3 或更高. 无其他SDK依赖. 安装方法 通过 OpenUPM 安装 ...
- composer源码简单分析(一)
composer分析(一) 本文内容 基于PSR-4规范的自动加载 请结合文档和下面的代码注释 spl_autoload_register php闭包Closure简单用法(大体使用情景: 生成回调提 ...
- 2020年B2B外贸建站的终极教程
本文目标:按照本建站教程的顺序操作,能够实现:基于全球份额最大的建站系统“wordpress”,从零搭建一个B2B外贸网站,且建站成本每年小于1000元(如果不计算自己投入的人力成本的话). 模板站点 ...
- Unity报与System.IO相关的错误
比如这个: Type `System.IO.FileInfo' does not contain a definition for `OpenText' and no extension method ...
- 初级知识点二——C#值传递
C#中有值传递和引用传递,这个东西一直有点儿绕,今天花点儿时间来把这个事情搞清楚. 传递值类型的参数 值类型的变量,是直接包含其数据的.实际上,在向方法传递一个值类型变量,其实就意味着向方法传递了一个 ...
- lombok配置
lombok在springboot中无需配置即可在控制台输出. 一般使用backlog.xml作为配置文件. 在application中指定backlog位置 不做任何配置时候,logback.xml ...
- vue init深度定制团队自己的Vue template
大家都知道,使用vue-cli可以快速的初始化一个基于Vue.js的项目,全局安装脚手架之后,你可以通过vue list命令看到官方提供的5个模板 vue list 当开发一个独立项目的时候,使用官方 ...
