在安装NX时，本机已经装了NX其他版本，只能修改当前程序，无法安装，那么多NX如何共存？

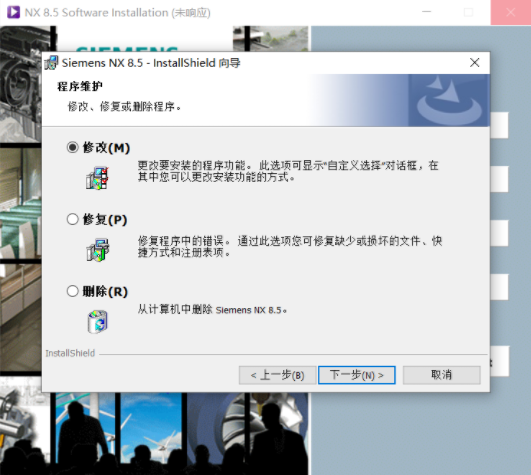
如图：先安装了32位NX8.5，后安装64位NX 8.5时弹的框。

解决办法有两种：
1）将已经安装的NX目录重命名，卸载NX，再安装新版本。
2）从其他人电脑上拷贝NX的安装目录至本机，只要license支持（若license不支持，请升级PLMLicenseServer），无需安装，也可使用。

两种方法任选其一均可解决，效果如下：

多NX如何共存的更多相关文章

  1. Linux服务器oraclejdk与openjdk共存并配置JavaEE开发环境

    由于本人学业的需要,需要在linux中搭建JavaEE开发环境,与windows的同学协同开发. JDK 由于fedora默认使用openjdk,移除多多少少会出现点问题,由于很多开源软件默认使用到它 ...

  2. COGS746. [网络流24题] 骑士共存

    骑士共存问题«问题描述:在一个n*n个方格的国际象棋棋盘上,马(骑士)可以攻击的棋盘方格如图所示.棋盘 上某些方格设置了障碍,骑士不得进入. «编程任务:对于给定的n*n个方格的国际象棋棋盘和障碍标志 ...

  3. 【wikioi】1922 骑士共存问题（网络流/二分图匹配）

    用匈牙利tle啊喂?和网络流不都是n^3的吗(匈牙利O(nm), isap O(n^2m) 但是isap实际复杂度很优的(二分图匹配中,dinic是O(sqrt(V)*E),不知道isap是不是一样. ...

  4. P3355 骑士共存问题

    P3355 骑士共存问题 题目描述 在一个 n*n (n <= 200)个方格的国际象棋棋盘上,马(骑士)可以攻击的棋盘方格如图所示.棋盘上某些方格设置了障碍,骑士不得进入 对于给定的 n*n ...

  5. P3355 骑士共存问题 二分建图 + 当前弧优化dinic

    P3355 骑士共存问题 题意: 也是一个棋盘,规则是“马”不能相互打到. 思路: 奇偶点分开,二分图建图,这道题要注意每个点可以跑八个方向,两边都可以跑,所以边 = 20 * n * n. 然后di ...

  6. APP多版本共存，服务端如何兼容？

    做过APP产品的技术人员都知道,APP应用属于一种C/S架构的,所以在做多版本兼容,升级等处理则比较麻烦,不像web应用那么容易.下面将带大家分析几种常见的情况和应对方式: 小改动或者新加功能的 这种 ...

  7. 设置Hyper-V和VMware多个服务之间共存

    这个方法是解决多个服务之间不能共存,下面相当于是以Hyper-V和VMware做例子,其他的也适用. 今天准备安装VMware Workstation 10,然后玩玩MAC OS. 没想到,淡定的我双 ...

  8. 让 FreeBSD 和 Gentoo Linux 在 ZFS 存储卷上共存

    自我回归到 Librem 15 已经有段时间了.我一般会选择 FreeBSD 来处理所有的事情,但有时会要访问一个运行在 Librem 平台上的 Linux OS,以便用它来帮助我对一些遗留的设备驱动 ...

  9. windows XP上实现python2.7.5和python3.4.3共存

    windows XP上实现python2.7.5和python3.4.3共存过程记录: 1. 首先安装python2.7.5和python3.4.3,两个版本安装顺序不分前后; 2. 检查系统环境变量 ...

随机推荐

  1. springMVC入门（七）------RESTFul风格的支持

    简介 RESTful风格(Representational State Transfer),又叫表现层状态转移,是一种开发理念,也是对HTTP协议很好的诠释 主要理念是将互联网中的网页.数据.服务都视 ...

  2. 算法-搜索（6）B树

    B树是平衡的m路搜索树. 根结点至少两个子女,根结点以外的非失败结点至少⌈m/2⌉个子女,所有失败结点都在h+1层. 第h层至少2⌈m/2⌉h-1个结点,因此失败结点数n+1≥2⌈m/2⌉h-1个. ...

  3. 手写一个简单版的SpringMVC

    一 写在前面 这是自己实现一个简单的具有SpringMVC功能的小Demo,主要实现效果是; 自己定义的实现效果是通过浏览器地址传一个name参数,打印“my name is”+name参数.不使用S ...

  4. 运用sed命令高效地删除文件的特定行

    运用 sed 命令高效地删除文件的特定行 正常来说,我们想要删除文件中的某些行内容,一般都是先打开这个文件,然后找到要删除的内容,再然后选中这些行并按删除键进行删除,这在数据量很少时是没有问题的.但是 ...

  5. 5. java 的类和对象

    1.什么是类 类 :是一组相关属性和行为的集合.可以看成是一类事物的模板,使用事物的属性特征和行为特征来描述该类事物.现实中,描述一类事物:属性 :就是该事物的状态信息.行为 :就是该事物能够做什么. ...

  6. CSP 202006-1 线性分类器python实现

    思路 这题问题是对于这一群点和一条直线,我们也不知道直线上方的是A类还是直线下方的是A类.其实对于这个二分类问题,我们也没必要知道.我们只需要判断直线每一测的点是不是一类(A类或B类)就可以了. 至于 ...

  7. Python字符串类型格式化之format方法

    python字符串格式化一般使用 format() 方法,用法如下: <模板字符串>.format(<逗号分割的参数>) 其中模板字符串中可以由一个或多个 {} 组成的 槽 , ...

  8. 图解Janusgraph系列-分布式id生成策略分析

    JanusGraph - 分布式id的生成策略 大家好,我是洋仔,JanusGraph图解系列文章,实时更新~ 本次更新时间:2020-9-1 文章为作者跟踪源码和查看官方文档整理,如有任何问题,请联 ...

  9. php反序列化总结与学习

    基础知识: 1.php类与对象 2.魔术函数 3.序列化方法 类与对象 <?php class test{ public $var = "hello world"; publ ...

  10. python-opencv 图像捕捉多个不规则轮廓，与轮廓内接区域(圆/矩形)思路-持续更新编辑中(会附上详细的思路解释和图片)

    整体思路: 1.原图灰度化 2.灰度图截取mask区域 3.mask区域二值化 4.二值化图像运算(开运算) 5.原灰图轮廓提取 6.不规则轮廓校准(外接矩形/内接矩形) 注:代码依次头尾连接哦! 0 ...