SP3267 DQUERY - D-query 莫队板子题

题意可见：https://www.luogu.com.cn/problem/SP3267

可在vj上提交：https://vjudge.net/problem/SPOJ-DQUERY

题意翻译

给出一个长度为n 的数列，a1,a2,a3,,,an ，有q 个询问，每个询问给出数对(i,j)，需要你给出ai，ai+1，ai+2...aj这一段中有多少不同的数字

输入输出样例

输入 #1复制

5
1 1 2 1 3
3
1 5
2 4
3 5

输出 #1复制

3
2
3

题解（推荐莫队讲解博客：https://www.cnblogs.com/WAMonster/p/10118934.html）：

我们可以用左指针和右指针在[1,n]这个区间上移动。题目给了q个询问区间，如果左指针和右指针和某个询问区间的左右边界对应，那就记录一下这个区间对应的结果。最后把所有结果都一起输出

因为询问区间的左右边界可能或大或小，那么我们的左右指针就会来回移动，这样很耗时间，我们可以先对n个数分块，然后对所有询问区间排序一下

int cmp(Node a,Node b)
{
    //正常是这样写
    //return belong[a.l] == belong[b.l] ? a.r < b.r : belong[a.l] < belong[b.l];
    //下面这样写的话可以优化时间，主要原理便是右指针跳完奇数块往回跳时在同一个方向能顺路把偶数块跳完，
    //然后跳完这个偶数块又能顺带把下一个奇数块跳完。理论上主算法运行时间减半
    return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r);
}

1、在指针移动过程中枚举到一个数值num，增加出现次数时判断一下cntnum是否为0，如果为0，则这个数值之前没有出现过，现在出现了，数值数当然要+1。反之在从区间中删除num后也判断一下cntnum是否为0，如果为0数值总数-1。

2、其次就是左右指针怎么移动了。假设这个序列是这样子的：（其中Q1Q1、Q2Q2是询问区间）

 

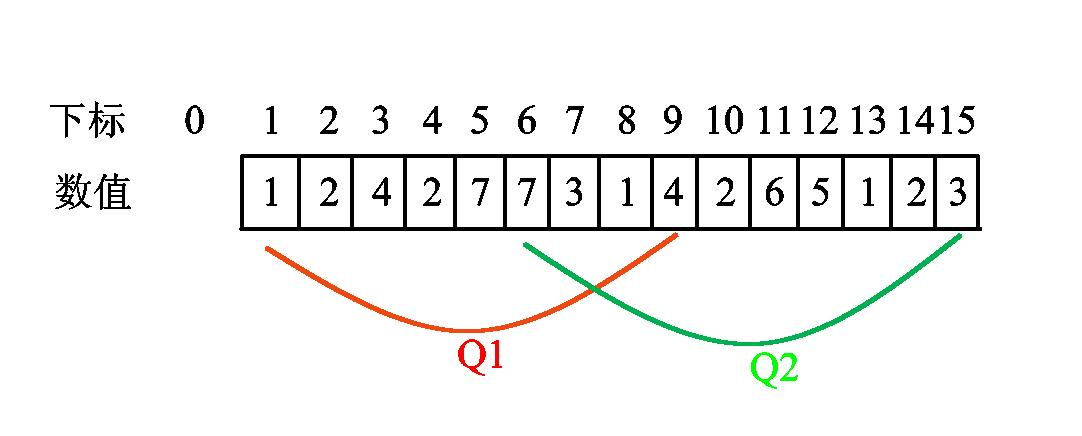
最初左指针在0位置，右指针在1位置，然后排序之后Q1区间肯定在前，所以我们肯定是先把左右指针移动到Q1区间的左右边界位置（下面是用L表示左指针，R表示右指针）

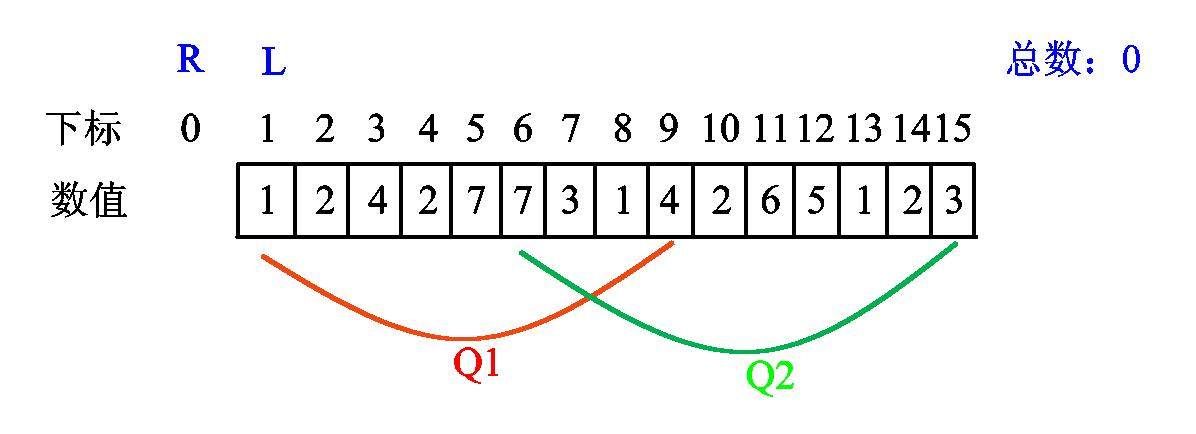
我们发现 l 已经是第一个查询区间的左端点，无需移动。现在我们将 r 右移一位，发现新数值1：

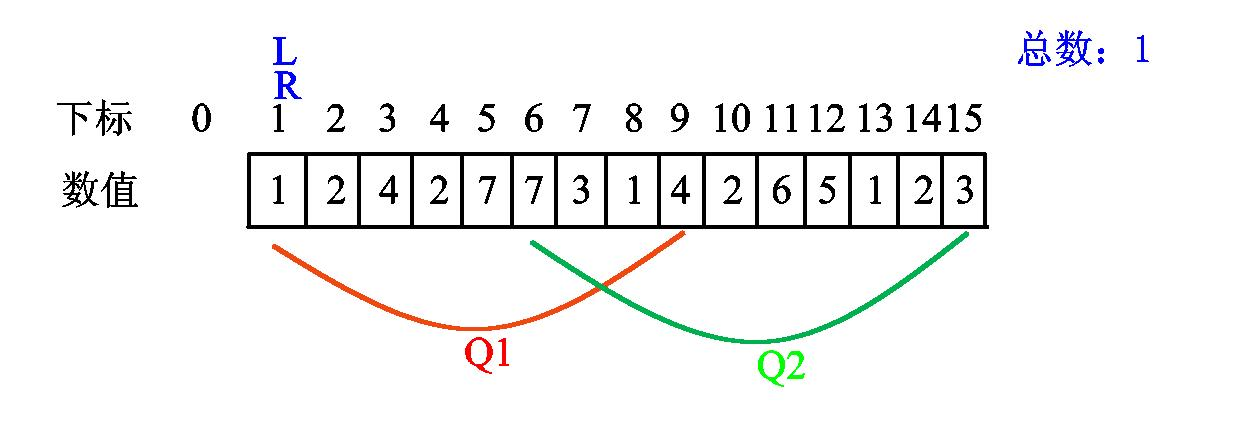
r 继续右移，发现新数值2：

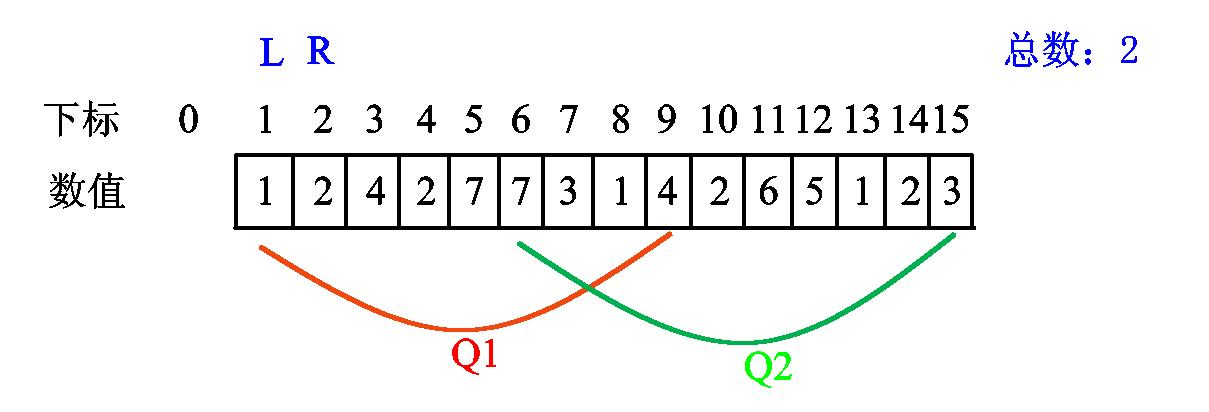
继续右移，发现新数值4：

当 r 再次右移时，发现此时的新位置中的数值2出现过，数值总数不增：

接下来是两个7，由于7没出现过，所以总数+1：

继续右移发现3：

继续右移，但接下来的两个数值都出现过，总数不增。

至此，Q1区间所有数值统计完成，结果为5。

现在我们又看一下Q2区间的情况：

首先我们发现， l 指针在Q2区间左端点的左边，我们需要将它右移，同时删除原位置的统计信息。

将l右移一位到位置2，删除位置1处的数值1。但由于操作后的区间中仍然有数值1存在，所以总数不减。

接下来的两位也是如此，直接删掉即可，总数不减。

当 l 指针继续右移时，发现一个问题：原位置上的数值是2，但是删除这个2后，此时的区间[l,r]中再也没有2了（回顾之前的内容，这种情况就是删除后cnt2=0），那么总数就要-1，因为有一个数值已经不在该区间内出现了，而本题需要统计的就是区间内的数值个数。此步骤如下图：

再右移一位，发现无需减总数，而且ll已经移到了Q2区间的左端点，无需继续移下去（如下图）。当然 r 还是要移动的，只不过没图了，我相信大家应该知道做法的qwq。

r的最后位置：

至于删除操作，也是一样的做法，只不过要先删除当前位置的数值，才能移动指针。

代码：

for(int i=1;i<=m;++i) //m就是排序之后的m个区间
    {
        int start=node[i].l,last=node[i].r;
        while(l<start) now-=!--cnt[arr[l++]];
        while(l>start) now+=!cnt[arr[--l]]++;
        while(r<last) now+=!cnt[arr[++r]]++;
        while(r>last) now-=!--cnt[arr[r--]];
        ans[node[i].id]=now;
    }

总的复杂度就是：n*√n

代码：

#include <map>
#include <set>
#include <list>
#include <queue>
#include <deque>
#include <cmath>
#include <stack>
#include <vector>
#include <bitset>
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 1e6+10;
const int INF = 0x3f3f3f3f;
const double PI = 3.1415926;
const long long N = 1000006;
const double eps = 1e-10;
typedef long long ll;
#define mem(A, B) memset(A, B, sizeof(A))
#define lson rt<<1 , L, mid
#define rson rt<<1|1 , mid + 1, R
#define ls rt<<1
#define rs rt<<1|1
#define SIS std::ios::sync_with_stdiget_mod_new(z-x)o(false), cin.tie(0), cout.tie(0)
#define pll pair<long long, long long>
#define lowbit(abcd) (abcd & (-abcd))
#define max(a, b) ((a > b) ? (a) : (b))
#define min(a, b) ((a < b) ? (a) : (b))
int arr[maxn],cnt[maxn],belong[maxn];
int n,m,sizes,new_size,now,ans[maxn];
struct Node{
    int l,r,id;
}node[maxn];
int cmp(Node a,Node b)
{
    //正常是这样写
    //return belong[a.l] == belong[b.l] ? a.r < b.r : belong[a.l] < belong[b.l];
    //下面这样写的话可以优化时间，主要原理便是右指针跳完奇数块往回跳时在同一个方向能顺路把偶数块跳完，
    //然后跳完这个偶数块又能顺带把下一个奇数块跳完。理论上主算法运行时间减半
    return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r);
}
int main()
{
    //printf("%d\n",(int)ceil(5.0));
    scanf("%d",&n);
    sizes=sqrt(n);
    new_size=ceil((double)n/sizes);
    for(int i=1;i<=new_size;++i)
    {
        for(int j=(i-1)*sizes+1;j<=i*sizes;++j)
        {
            belong[j]=i;
        }
    }
    for(int i=1;i<=n;++i)
    {
        scanf("%d",&arr[i]);
    }
    scanf("%d",&m);
    for(int i=1;i<=m;++i)
    {
        scanf("%d%d",&node[i].l,&node[i].r);
        node[i].id=i;
    }
    sort(node+1,node+1+m,cmp);
    int l=1,r=0,now=0;
    for(int i=1;i<=m;++i)
    {
        int start=node[i].l,last=node[i].r;
        while(l<start) now-=!--cnt[arr[l++]];
        while(l>start) now+=!cnt[arr[--l]]++;
        while(r<last) now+=!cnt[arr[++r]]++;
        while(r>last) now-=!--cnt[arr[r--]];
        ans[node[i].id]=now;
    }
    for(int i=1;i<=m;++i) printf("%d\n",ans[i]);
    return 0;
}

卡常：

1、#pragma GCC optimize(2)

可以用实践证明，开了O2的莫队简直跑得飞快，连1e6都能无压力跑过，甚至可以比不开O2的版本快上4~5倍乃至更多。然而部分OI比赛中O2是禁止的，如果不禁O2的话，那还是开着吧qwq

实在不行，就optimize(3)（逃