用试探回溯法解决N皇后问题

学校数据结构的课程实验之一。

数据结构：（其实只用了一个二维数组）

算法：深度优先搜索，试探回溯

需求分析：

　　设计一个在控制台窗口运行的“n皇后问题”解决方案生成器，要求实现以下功能：

　　由n*n个方块排成n行n列的正方形称为n元棋盘。如果两个皇后位于n元棋盘上的同一行、同一列或同一对角线上，则称它们在互相攻击。现要找出使棋盘上n个皇后互不攻击的布局。

　　编制程序解决上述问题，以n=6运行程序，输出结果。

算法解释：

　　首先试探当前行第一个可用的位置（列、对角线没有被占领），摆放皇后之后，试探下一行的第一个可用位置；如果遇到此行没有可用位置，则返回上一行，移除上一行的皇后，试探此行的下一个可用位置，直至n个皇后全部摆放好，生成一种方案。

主函数：

 int main()
 /*Pre: The user enters a valid board size.
 Post: All solutions to the n-queens puzzle for the selected board size
 are printed.
 Uses: The class Queens and the recursive functionsolve from. */
 {
     int board_size;
     char choice = 'y';
     char enter;
     while (choice == 'y')//由用户决定是否继续
     {
         sum = ;
         cout << "What is the size of the board?"<<flush;
         cin >> board_size;
         if(board_size < ||board_size > max_board)
             cout<<"The number must between 0 and "<<max_board<<endl;
         else
         {
             Queens configuration(board_size);//创建size*size的对象
 
             cout << "there is total " << solve_from(configuration) << " configurations." << endl;//打印所有解决方案和方案个数
         }
         cout << endl << "Would you like to continue? [y/n]" << endl;
         //回车符的消去
         fflush(stdin);
         while ((enter = cin.get()) == '\n')
         {
             enter = cin.get();
         }
         cin.putback(enter);
         cin >> choice;//移植了计算器的代码
     }
     return ;
 }

辅助函数（计算出所有解决方案）(参考了经典教材"Data Structures and Program Design in C++" Robert L. Kruse, Alexander J. Ryba 高等教育出版社-影印版)

 int sum = ;//记录解决方案个数
 
 int solve_from(Queens &configuration)//通过递归、回溯找到所有解决方案并打印
 /*Pre: the queens configuration represents a partially completed
 arrangement of nonattacking queens on a chessboard.
 Post: all n-queens solutions that extend the given configuration are
 printed. The configuration is restored to its initial state.
 Uses: the class Queens and the function solve_from, recursively.*/
 {
     if (configuration.is_solved())//当生成一种解决方案时打印，sum自增一
     {
         sum++;
         configuration.print();
         cout <<"================" <<endl;
     }
     else
         for(int col=; col<configuration.board_size; col++)
             if(configuration.unguarded(col))
             {
                 configuration.insert(col);
                 solve_from(configuration);//recursively continue to add queens当生成一种解决方案时打印
                 configuration.remove(col);//return the last row and the last col.试探上一层的下一种方案（无论上一次试探是成功还是失败）
             }
     return sum;
 }

注：

　　每次回溯其实有两种可能：“摆放满了n个皇后”或者“此行没有可放的位置”，二者都会返回上一行去试探下一种可能，只不过摆满n个皇后的情况会生成一种方案（被if截获，回到上一层循环），生成后还是回到倒数第二行再进行试探。因此一次深度优先搜索（调用一次solve_from函数）可以将所有方案全部输出。

“皇后”类的定义

 const int max_board = ;//最大棋盘阶数
 using namespace std;
 
 class Queens
 {
 public:
     Queens(int size);
     bool is_solved() const;//判断是否完成一种方案
     void print() const;//打印当前方案
     bool unguarded(int col) const;//判断某格是否可放皇后
     void insert(int col);//摆放皇后
     void remove(int col);//移除
     int board_size;//dimension of board = maximum number of queens
 private:
     int count;//current number of queens = first unoccupied row
     bool queen_square[max_board][max_board];//存放棋盘状态的二维数组
 };

“皇后”类的实现(同样参考了经典教材"Data Structures and Program Design in C++" Robert L. Kruse, Alexander J. Ryba 高等教育出版社-影印版)

 #include <iostream>
 #include "Queens.h"
 
 Queens::Queens(int size)
 {
     board_size = size;
     count = ;//从第一行开始计数
     for(int row=; row<board_size; row++)
         for(int col=; col<board_size; col++)
             queen_square[row][col] = false;//生成size*size的空棋盘
 }
 
 bool Queens::is_solved() const
 /*whether the number of queens already placed
 equals board_size*/
 {
     bool solved = false;
     if(count == board_size)//当board_size个皇后都摆放完毕时，生成一种方案
         solved = true;
     return solved;
 }
 
 void Queens::print() const
 {
     for (int row = ; row < board_size; row++)
     {
         for (int col = ; col < board_size; col++)
             if (queen_square[row][col] == true)
                 cout << "* ";
             else
                 cout << "_ ";//逐个打印棋盘元素，有皇后打印'*'，无皇后打印'_'
         cout << endl;
     }
 }
 
 bool Queens::unguarded(int col) const
 /*Post: Return true or false according as the square in the first
 unoccupied row(row count) and colum col is not guarded by andy queen*/
 {
     int i;
     bool ok = true;//turn false if we find a queen in column or diagonal
     for(i=; ok && i < count; i++)
         ok = !queen_square[i][col];//check upper part of column同列
     for(i=; ok && count-i >=  && col-i >=; i++)
         ok = !queen_square[count-i][col-i];//check upper-left diagonal
     for(i=; ok && count-i >=  && col+i < board_size; i++)
         ok = !queen_square[count-i][col+i];//chekck upper-right diagonal
     return ok;
 }
 
 void Queens::insert(int col)
 /*Pre: The square in the first unoccupied row(row count) and column is not
 guarded by any queen.
 Post: A queen has been inserted into the square at row count and column col;
 count has been incremented by 1*/
 {
     queen_square[count++][col] = true;//放入皇后，计数器自增一（到下一行）
 }
 
 void Queens::remove(int col)
 /*Pre: there is a queen in the square in row count-1 and column col.
 Post: the above queen has been removed; count has been decremented by 1.*/
 {
     queen_square[count-][col] = false;//移出皇后，计数器自减一（回上一行）
     count--;
 }

Queen.cpp

运行截图：

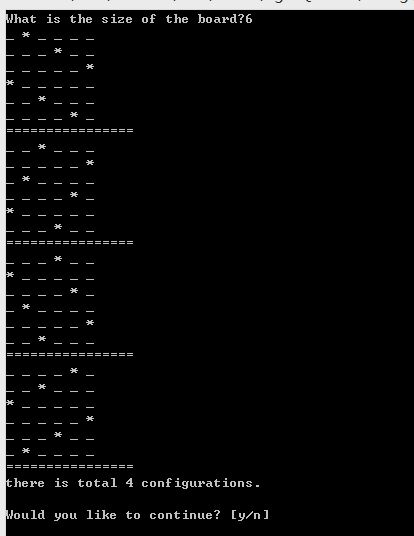
注：

　　当输入的棋盘阶数比较大（如：8）时，命令行窗口的缓冲区默认300行可能会不够显示，所以要在属性修改“高度”，使所有结果都显示出来。