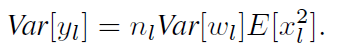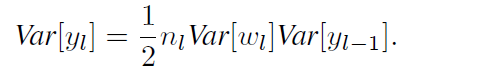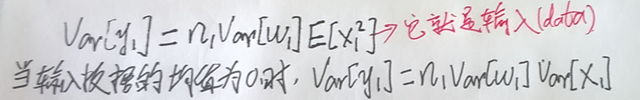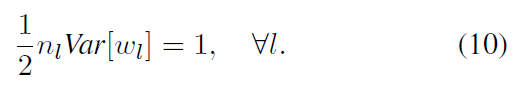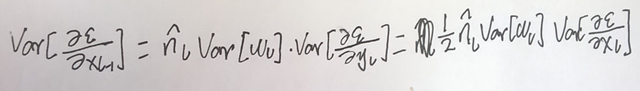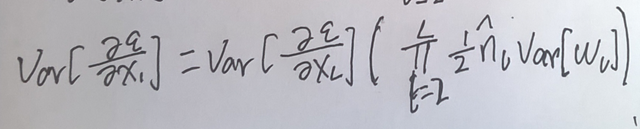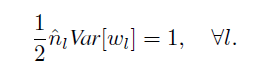微软亚洲实验室一篇超过人类识别率的论文:Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification ImageNet Classification
在该文章的两大创新点:一个是PReLU,一个是权值初始化的方法。下面我们分别一一来看。
PReLU(paramter ReLU)
所谓的PRelu,即在 ReLU激活函数的基础上加入了一个参数,看一个图就明白了:
右边的图上多了一个参数吧,在负半轴上不再为0,而是一个可以学习的斜率。 很容易明白。实验结果显示该方法可以提高识别率。
权值初始化的方法:
对于文中的权值初始化问题:主要思想是跟随了“Xavier”的初始化的思想,研究了第一层layer的响应的 variance。下面的推导过程是基于ReLU激活函数的。 分为一下两种情况来分析:
forward propagation:
在推导前,先说一些符号的代表意义:yL表示第L层上的一个feature map上的一个神经单元的response(这里的response指的是上一层的所有连接单元的加权和,是不经过激活函数哈,这里把激活函数作另外的一个行为吧);yL 经过激活函数看得到的值我们记作XL; bL表示偏置;L层的feature map的个数用 dL表示; 卷积核的大小表示为k*K(可能不同的layer的卷积核不一样哦,这里就不区分了); 激活函数表示为f();
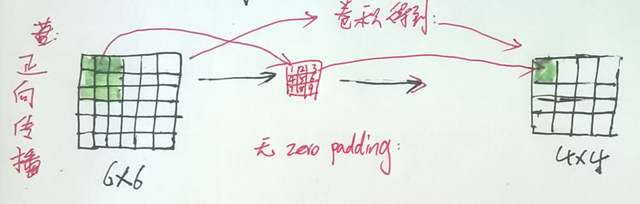
以下为正向传播的卷积过程(只画出了一个feature map的情况) :
其中一个输出值用公式表示 如下(接收域的feature map 的个数为 dL-1) :
接下来呢,我们会这么做:
1. 初始化时,我们把权值WL里的各元素 初始化为独立同分布的变量,且令 WL 的均值为 0 ;
2. 我们假设元素 XL 的变量也是独立同分布的变量;
3. WL 与 XL 是相互独立的;
往下的推导会用于以下概率论中的知识:
对于随机变量X,它的期望可以表示为EX,下面看看它的方差怎么表示:
DX = E(X-EX)2 = E(X2-2XEX +(EX)2) = EX2 - (EX)2
所以当 EX=0时,DX = EX2
当随机变量X与随机变量Y相互独立时,我们有这样的结论:
EXY = EX * EY
DXY = EX2EY2 –(EX)2(EY)2
D(X+Y) = DX + DY
在上面的条件下我们继续推导,推导的核心为求 response 的 方差(variance):
所以就得到了:
然后呢,我们让W L-1 的对称分布在0值的左右,这样同时也就可以让 W 的均值为0 (或期望为0)了,然后,这样的话, y L-1 的分布也是对称分布在0值左右了。y L-1 的期望也为0 了。所以就有了下面的结果:
代入到上面公式中得到:
把L层的layer 联合起来,我们可以得:
为了使 y1 的方差与 yL 的方差相等,我们就需要另:
,其中 l = 2, 3, 4, …… L。
对于第一层的输入,我们有这样的公式:
所以第一层对应的条件为:
为了各层之间 统一起来, 第一层差个1/2也没事,所以呢,对于前向传导,权值应该满足这样的条件:
其中:
,K 为第K层的卷积核的大小。
结论: 权值满足 mean 为0, 方差为 2/ nl 的条件.
Backward Propagation :
对于反向传播时,利用BP算法,当我们在推导公式中,总要求出目标函数对每一层的输入值的 偏导数。下面的公式如果你没有推导过这个BP过程的话,可能有点看不懂哦:
上面的公式可能和论文里的有点不一样,因为吧,论文里一次性把多个feature map上的对应元素求出来了,我觉得对于下面的推导,求一个就够 了。对于上面公式的过程,我自己画了一个图表示一下 :
对上图的说明:1,我只画出了一个 feature map的情况;2,还有注意卷积核,与正向传播时的卷积核有差别(旋转了180度);3,卷积的对象以及输出的对象都是偏导数;4,可以与正向传播时作个对比;
下面为推导过程,也是围绕着 方差来的:
然后,就得到了:
当我们把L层合在一起时,变为了:
当然,对于X0(它表示网络的输入)没有必要去求偏导数,但是为了推出第一层网络权值满足的条件,我们也可以写出来:
,它同样符合公式的哦,我已经证明过了。。。
对于前向传导时,在第一层会有一个1/2的差别,但是在这反向传播中没有。其实反射传播也存在一层的差别,只不过是在L+1层,因为在第L层往后可能没有激活函数了。
所以呢,在反向传播过程中,为了使偏对数的方差相同的话,那么需要满足的条件为:
,K 为第L层的卷积核。
注意了正向与反向的差别了吧,为了均衡正向与反向传播,我们可以取其平均值哦。
文章后面的话,就是一些实验的安排了。。其实对于VLIRC 任务来说,实验部分其实都基本上吧方法类似的。
文章一方面说,他的初始化方法可以做到对于深层的网络训练时起来收敛的作用, 一方面又说了,很多时候一味地增加网络的深度并不一定可以使网络的性能提高(这个也在很多其它的文献中有说的了)。所以呢,网络的设计吧,还是一个难题啊。
另外,从文中看到一个新的pooling 方法: spatial pyramid pooling. 它来自文献: Spatial pyramid pooling in deep convolutional networks for visual recognition。
总之呢,文章最大亮点大于:Prelu 和 权值初始化的方法。 如果有什么问题与错误,大家可以在评论区写下来,我相互讨论学习进步。
微软亚洲实验室一篇超过人类识别率的论文:Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification ImageNet Classification的更多相关文章
- 探索真实事物的虚拟再现——微软亚洲研究院SIGGRAPH Asia 2014精彩入选论文赏析
Asia 2014精彩入选论文赏析" title="探索真实事物的虚拟再现--微软亚洲研究院SIGGRAPH Asia 2014精彩入选论文赏析"> SIGGRAP ...
- 微软亚洲研究院的“哈利·波特”:Thomas Moscibroda
在微软亚洲研究院,有一位名为Thomas Moscibroda的研究员几乎是无人不知.无人不晓,江湖人送外号"哈利·波特".Thomas认为他这么"红"是因为他 ...
- 微软亚洲研究院研究员获选IEEE Fellow 和ACM Distinguished Member
年末将至,微软亚洲研究院喜讯连连.近日,IEEE(国际电气电子工程师学会)和ACM(美国计算机协会)先后公布了2017年度的院士名单(IEEE Fellow)和2016年度杰出会员名单(ACM D ...
- Ta说:2016微软亚洲研究院第二届博士生论坛
"聚合多元人才创造无尽可能,让每一位优秀博士生得到发声成长机会"可以说是这次微软亚洲研究院博士生论坛最好的归纳了.自去年首次举办以来,这项旨在助力青年研究者成长的项目迅速得到了 ...
- 学一手,知乎大V(轮子哥)当年靠它进微软亚洲研究院
前言 vczh本名陈梓瀚,不过大家更愿意叫他「轮子哥」,毕业于华南理工大学软件学院.vczh大学时代就在微软实习,毕业后即加入微软.开始时是在微软上海,后来进入北京的微软亚洲研究院.现已移居美国西雅图 ...
- 深度卷积网络(DCNN)和人类识别物体方法的不同
加州大学洛杉矶分校在PLOS Computing Biology上发表了一篇文章,分析了深度卷积网络(DCNN)和人类识别物体方法的不同:深度卷积网络(DCNN)是依靠物体的纹理进行识别,而人类是依靠 ...
- 科研伴我成长——上海交通大学ACM班学生在微软亚洲研究院的幸福实习生活
每一年,微软亚洲研究院都会迎来一批"特殊的"实习生--他们既不是从五湖四海汇聚而来,也不是在读的硕士和博士.他们相识已久,知道对方的小秘密.小八卦,也相互敬佩.惺惺相惜--他们就是 ...
- 解密优秀博士成长史 ——微软亚洲研究院首届博士生学术论坛Panel讨论经验总结
编者按:有人说“一入博门深似海”,读博前应该做好哪些准备?作为一名博士生,应该有怎样的学术或职业规划?导师还是老板?怎样在师生关系上做到双赢?你是导师心目中优秀的博士生吗?相信以上问题在很多同学心中萦 ...
- Offer垂青于有准备的人——微软亚洲研究院实习生们的就业分享
编者按:一年一度的"求职大战"又拉开了序幕,如何在求职中掌握主动,更好地展现自己,最后抓住Offer?且听微软亚洲研究院三位实习生慢慢道来,Offer总会垂青于有准备的人. 廖振, ...
随机推荐
- JS调用OC方法并传值,OC调用JS方法并传值////////////////////////zz
iOS开发-基于原生JS与OC方法互相调用并传值(附HTML代码) 最近项目里面有有个商品活动界面,要与web端传值,将用户在网页点击的商品id 传给客户端,也就是js交互,其实再说明白一点 ...
- c#:如何处理对对象进行深度拷贝
/// <summary> /// 对对象进行深度拷贝 /// </summary> /// <param name="obj"></pa ...
- 修改后的CopyFile类
这是修改后的CopyFile类,前面那个类有局限性,它不能复制大文件 这是我第一次写成一个能够实际应用的类,感谢博主们的无私奉献,感谢SeayXu老师的提点 但是这个类也并不是完美无缺,它复制文件没有 ...
- web app响应式字体设置!rem之我见
之前做沙漠教育的时候,直接以设计图为准,然后强暴式,缩放处理.简单.直接,粗暴!但是,开发快.……一劳永逸! 但那是,现在开发,作为业界良心:是不能那么做的!(那个是被逼的啊 首先看代码: @medi ...
- Java数据结构之字符串模式匹配算法---KMP算法
本文主要的思路都是参考http://kb.cnblogs.com/page/176818/ 如有冒犯请告知,多谢. 一.KMP算法 KMP算法可以在O(n+m)的时间数量级上完成串的模式匹配操作,其基 ...
- ASP.NET MVC中viewData、viewBag和templateData的区别
在MVC3开始,视图数据可以通过ViewBag属性访问,在MVC2中则是使用ViewData.MVC3中保留了ViewData的使用.ViewBag是动态类型(dynamic),ViewData是一个 ...
- 5. 网络配置与FTP服务笔记
IP地址: Ipv4 2*32 Ipv6 tcp 网络通讯协议 udp 用户数据报协议 常见网络端口: 20 21 ftp服务 文件共享 22 ...
- mha配置参数详解
mha配置参数详解: 参数名字 是否必须 参数作用域 默认值 示例 hostname Yes Local Only - hostname=mysql_server1, hostname=192.168 ...
- [linux系统]查看内核版本和系统版本方法
查看内核版本信息的两个命令: uname -a cat /proc/version 查看系统版本的命令: lsb_release -a more /etc/issue cat /etc/redhat- ...
- easyui关于validatebox实现多重规则验证的实践
参考资料 http://blog.csdn.net/jumtre/article/details/38510975 http://blog.csdn.net/lybwwp/article/detail ...