SPSS-方差分析
方差分析(单因素方差分析、多因素方差分析、协方差分析)
基本概念:进行两组以上均数的比较,检验两个或两个以上样本均数差别的显著性(T检验主要是检验两个样本均数差别的显著性)
基本思想:通过分析不同变量的变异对总变异的贡献大小,确定控制变量对研究结果影响力的大小
前提条件:不同水平下各总体均值服从方差相同的正态分布
1.单因素方差分析:测试某一控制变量的不同水平是否给观察变量造成了显著差异和变动
计算:F检验
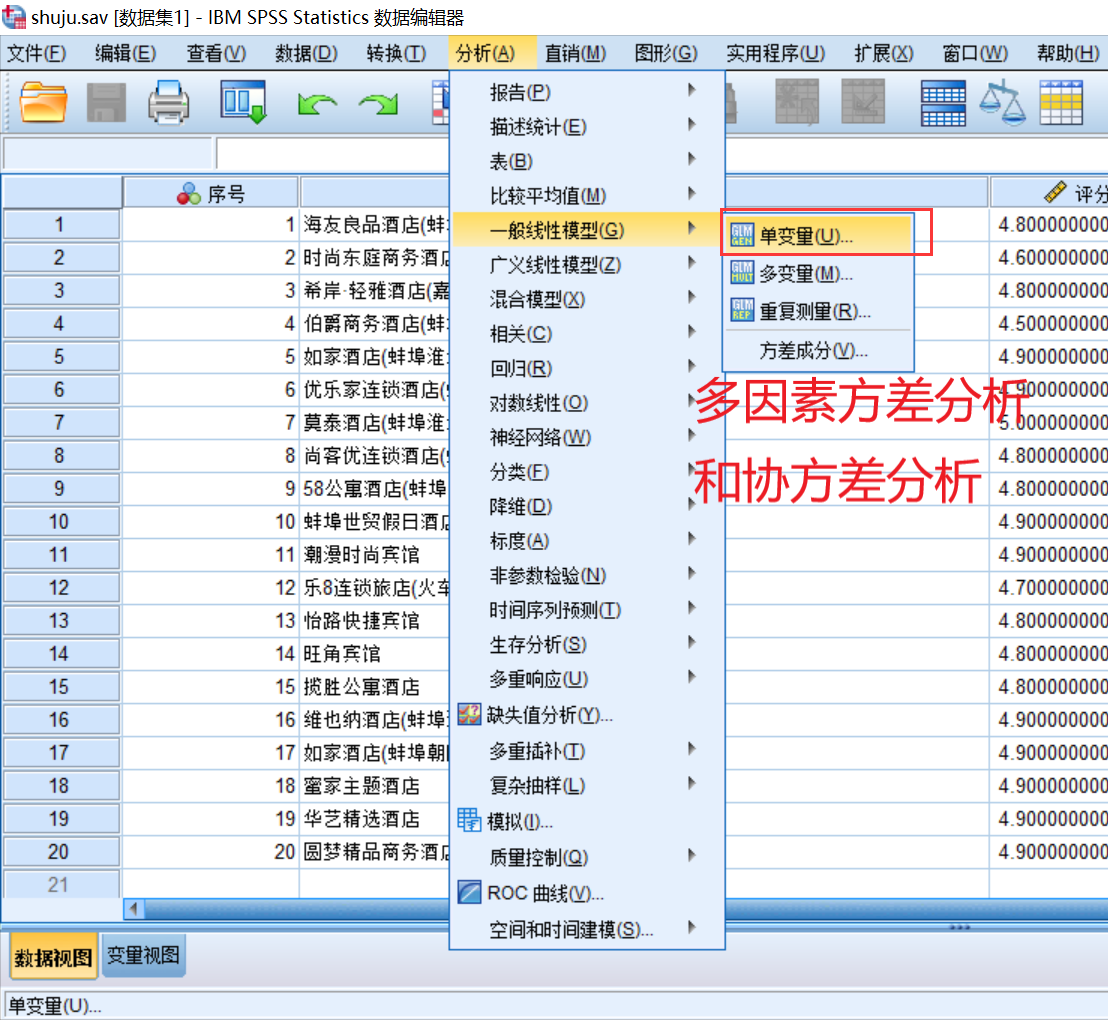
2.多因素方差分析:分析多个控制变量的作用、多个控制变量的交互作用以及其他随机变量是否对结果产生了显著影响
计算:将观察变量总的离差平方和分解为3各部分:多个控制变量单独作用引起的平方和;多个控制变量交互作用引起的离差平方和;其他随机因素引起的离差平方 和
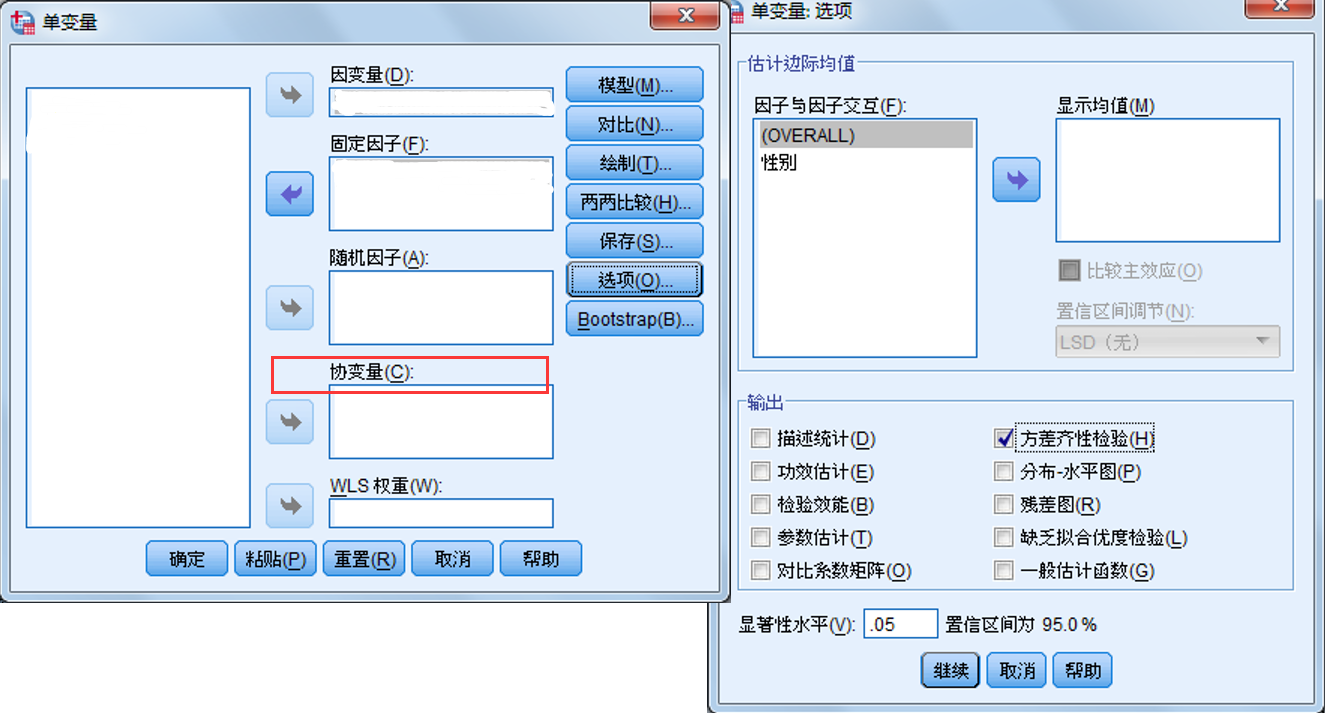
3.协方差分析:将很难控制的因素作为协变量,在派出协变量影响的条件下,分析控制变量对观察变量的影响
要求:协变量是连续数值型,多个协变量间相互独立,且与控制变量之间也没有交互影响
注:单因素和多因素方差分析中的控制变量都是定性变量,而协方差分析中既包含定性变量(控制变量),也包含定量变量(协变量)
SPSS操作
1.单因素方差分析




2.多因素方差分析和协方差分析
SPSS-方差分析的更多相关文章
- SPSS方差分析
1.overall:一切的,全面地 单因素方差分析:分析--比较均值--单因素ANOVA.多因素方差分析:分析--一般线性模型--单变量. 单因素方差分析和单变量方差分析区别:单因素针对的是自变量(自 ...
- SPSS数据分析—单因素及多因素方差分析
t检验可以解决单样本.两个样本时的均值比较问题,但是对于两个以上样本,就不能用t检验了,而要使用方差分析.t检验是借助t分布,方差分析是借助F分布,基于变异分解的思想进行. 在算法上,由于线性模型的引 ...
- 使用spss做方差分析
还记得上学那会老师专门敲了黑板,强调方差分析很重要..单因素方差分析(Analysis of Variance, ANOVA),如果变量多,就是多因素方差分析,还需要考虑到多重共线性, 也就是线性代数 ...
- SPSS基础学习方差分析—单因素分析
为什么要进行方差分析? 单样本.两样本t检验其最终目的都是分析两组数据间是否存在显著性差异,但如果要分析多组数据间是否存在显著性差异就很困难,因此用方差分析解决这个问题:举例:t检验可以分析一个班男女 ...
- SPSS分析技术:多元方差分析
SPSS分析技术:多元方差分析 下面要介绍多元方差分析的内容,多元方差分析是研究多个自变量与多个因变量相互关系的一种统计理论方法,又称多变量分析.多元方差分析实质上是单因变量方差分析(包括单因素和多因 ...
- SPSS统计分析案例:无空白列重复正交试验设计方差分析
SPSS统计分析案例:无空白列重复正交试验设计方差分析 前面有讲过 SPSS正交试验设计及其方差分析 一篇文章,包含了一个典型的正交试验案例.然而在实际应用当中,主观客观条件复杂多变,在试验设计中就要 ...
- SPSS数据分析—多元方差分析
之前的单因素方差分析和多因素方差分析,都在针对一个因变量,而实际工作中,经常会碰到多个因变量的情况,如果单纯的将其拆分为多个单因变量的做法不妥,需要使用多元方差分析或因子分析 多元方差分析与一元方差分 ...
- Hotelling T2检验和多元方差分析
1.1 Hotelling T2检验 Hotelling T2检验是一种常用多变量检验方法,是单变量检验的自然推广,常用于两组均向量的比较. 设两个含量分析为n,m的样本来自具有公共协方差阵的q维正态 ...
- SPSS中两种重复测量资料分析过程的比较
在SPSS中,有两个过程可以对重复测量资料进行分析:一种是一般线性模型的重复度量:一种是混合线性模型,对于同样的数据资料,使用两种过程分析出的内容不大一样,注意是内容而不是结果,只要操作正确,结果应该 ...
- SPSS数据分析—广义线性模型
我们前面介绍的一般线性模型.Logistic回归模型.对数线性模型.Poisson回归模型等,实际上均属于广义线性模型的范畴,广义 线性模型包含的范围非常广泛,原因在于其对于因变量.因变量的概率分布等 ...
随机推荐
- Solr高效利用:Solr实现SQL的查询与统计
1.如何高效使用Solr查询功能 ?2.单个字段分组统计如何实现? 3.IN条件查询有几种方式? 4.多个字段分组统计是否只支持count? Cloudera公司已经推出了基于Hadoop平台的查询统 ...
- Django跨域问题
相关博客地址 同源策略与Jsonp 同源策略 同源策略(Same origin policy)是一种约定,它是浏览器最核心也最基本的安全功能,如果缺少了同源策略,则浏览器的正常功能可能都会受到影响.可 ...
- 微信小程序如何引用其他js文件
1.我们先建立一个common.js文件,在common.js编写我们的程序, function myfunc() { console.log("myfunc....");} mo ...
- 完全使用css编写复选框
在日常的项目中,出现复选框或者单选框,应该都属于常见需求了,最开始阶段,一般只有两种可能性: 一.完全使用 <input type="checkbox" />或者&l ...
- 34.纯 CSS 创作在文本前后穿梭的边框
原文地址: https://segmentfault.com/a/1190000015045700 感想: 动画 + z-index:n ; HTML code: <div class= ...
- 《算法》第一章部分程序 part 1
▶ 书中第一章部分程序,加上自己补充的代码,包括若干种二分搜索,寻找图上连通分量数的两种算法 ● 代码,二分搜索 package package01; import java.util.Arrays; ...
- zookeeper(1)初识zookeeper
一.zookeeper的安装 1.下载zookeeper(当然在安装zookeeper之前得先装好jdk,这里就不说了),版本自己随便选一个(后面我再说版本的问题),点击这里下载. 2.然后在usr下 ...
- Kettle入门
kettle 水壶 正如其名“水壶”,将各个地方的水倒进水壶里,再用水壶倒入不同的容器. 勺子-Spoon.bat/spoon.sh 图形界面工具,就是启动上图主界面的命令行. ketchen 厨房 ...
- 查看进程中的socket状态和数量
程序运行时查看,结果是这样子的 C:\Users\Administrator>netstat -ano|findstr TCP TIME_WAIT TCP TIME_WAIT TCP TIME_ ...
- 浅谈 volatile 的实现原理
在并发编程中我们一般都会遇到这三个基本概念:原子性.可见性.有序性.我们稍微看下volatile 原子性 原子性:即一个操作或者多个操作 要么全部执行并且执行的过程不会被任何因素打断,要么就都不执行. ...
