《C++数据结构-快速拾遗》 树结构

---

1.简单的二叉树结构

 #include <iostream>
 using namespace std;
 typedef int DATA;

 //建立二叉树的简单结构
 typedef struct SNode
 {
     DATA data;
     SNode *pLeft,*pRight;
     SNode(DATA d):data(d)//构造函数为了初始化方便
     {
         pLeft  = NULL;
         pRight = NULL;
     }
 }SNode;

 int main(int argc,char*argv[])
 {
     SNode* p  = new SNode();
     p->pLeft  = new SNode();
     p->pRight = new SNode();
     cout<<p->data<<endl<<p->pLeft->data<<endl<<p->pRight->data<<endl;
     cout<<"hello deepin";
     return ;
 }

 #include <iostream>
 using namespace std;
 typedef int DATA;

 //建立二叉树的简单结构
 typedef struct SNode
 {
     DATA data;
     SNode *pLeft,*pRight;
     SNode(DATA d):data(d)//构造函数为了初始化方便
     {
         pLeft  = NULL;
         pRight = NULL;
     }
 }SNode;
 SNode* m_pRoot = NULL;//如果不定义全局变量，就需要通过函数参数传递
 void AddData()
 {
     //第一层
     SNode* p  = new SNode();
     m_pRoot = p;
     //第二层
     m_pRoot->pLeft  = new SNode();
     m_pRoot->pRight = new SNode();
     //第三层
     m_pRoot->pLeft->pLeft   = new SNode();
     m_pRoot->pLeft->pRight  = new SNode();
     m_pRoot->pRight->pLeft  = new SNode();
     m_pRoot->pRight->pRight = new SNode();
     //第四层
     m_pRoot->pLeft->pLeft->pLeft  = new SNode();
     m_pRoot->pLeft->pRight->pLeft = new SNode();
 }

 int main(int argc,char*argv[])
 {
     cout<<m_pRoot->data<<endl<<m_pRoot->pLeft->data<<endl<<m_pRoot->pRight->data<<endl
         <<m_pRoot->pLeft->pLeft->data<<endl<<m_pRoot->pLeft->pRight->data<<endl<<m_pRoot->pRight->pLeft->data<<endl
         <<m_pRoot->pRight->pRight->data<<endl<<m_pRoot->pLeft->pLeft->pLeft->data<<endl
         <<m_pRoot->pLeft->pRight->pLeft->data<<endl;
     cout<<"hello deepin";
     return ;
 }

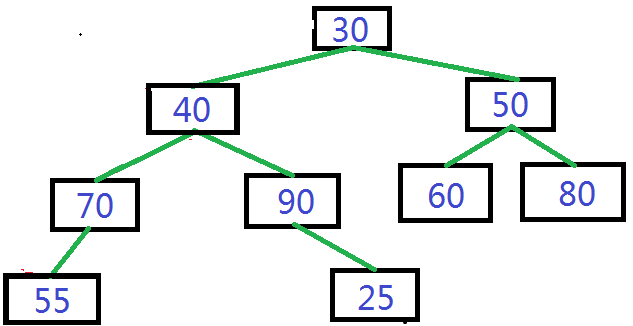
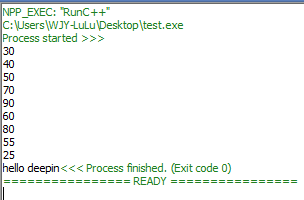
2.前序遍历

 #include <iostream>
 using namespace std;
 typedef int DATA;

 //建立二叉树的简单结构
 typedef struct SNode
 {
     DATA data;
     SNode *pLeft,*pRight;
     SNode(DATA d):data(d)//构造函数为了初始化方便
     {
         pLeft  = NULL;
         pRight = NULL;
     }
 }SNode;
 SNode* m_pRoot = NULL;//如果不定义全局变量，就需要通过函数参数传递
 void AddData()
 {
     //第一层
     SNode* p  = new SNode();
     m_pRoot = p;
     //第二层
     m_pRoot->pLeft  = new SNode();
     m_pRoot->pRight = new SNode();
     //第三层
     m_pRoot->pLeft->pLeft   = new SNode();
     m_pRoot->pLeft->pRight  = new SNode();
     m_pRoot->pRight->pLeft  = new SNode();
     m_pRoot->pRight->pRight = new SNode();
     //第四层
     m_pRoot->pLeft->pLeft->pLeft  = new SNode();
     m_pRoot->pLeft->pRight->pLeft = new SNode();
 }
 void FPrint(SNode* pRoot)
 {
     //SNode* p = m_pRoot;
     if(!pRoot) return;
     cout<<pRoot->data<<endl;
     //递归调用本函数实现打印
     if(pRoot->pLeft)
         FPrint(pRoot->pLeft);
     if(pRoot->pRight)
         FPrint(pRoot->pRight);
 }
 int main(int argc,char*argv[])
 {
     AddData();
     FPrint(m_pRoot);
     cout<<"hello deepin";
     return ;

 }

3.中序遍历

 #include <iostream>
 using namespace std;
 typedef int DATA;

 //建立二叉树的简单结构
 typedef struct SNode
 {
     DATA data;
     SNode *pLeft,*pRight;
     SNode(DATA d):data(d)//构造函数为了初始化方便
     {
         pLeft  = NULL;
         pRight = NULL;
     }
 }SNode;
 SNode* m_pRoot = NULL;//如果不定义全局变量，就需要通过函数参数传递
 void AddData()
 {
     //第一层
     SNode* p  = new SNode();
     m_pRoot = p;
     //第二层
     m_pRoot->pLeft  = new SNode();
     m_pRoot->pRight = new SNode();
     //第三层
     m_pRoot->pLeft->pLeft   = new SNode();
     m_pRoot->pLeft->pRight  = new SNode();
     m_pRoot->pRight->pLeft  = new SNode();
     m_pRoot->pRight->pRight = new SNode();
     //第四层
     m_pRoot->pLeft->pLeft->pLeft  = new SNode();
     m_pRoot->pLeft->pRight->pLeft = new SNode();
 }
 //中序遍历
 void MPrint(SNode* pRoot)
 {
     if(!pRoot) return;
     if(pRoot->pLeft)
         MPrint(pRoot->pLeft);
     cout<<pRoot->data<<endl;
     //递归调用本函数实现打印
     if(pRoot->pRight)
         MPrint(pRoot->pRight);
 }
 int main(int argc,char*argv[])
 {
     AddData();
     MPrint(m_pRoot);
     cout<<"hello deepin";
     return ;

 }

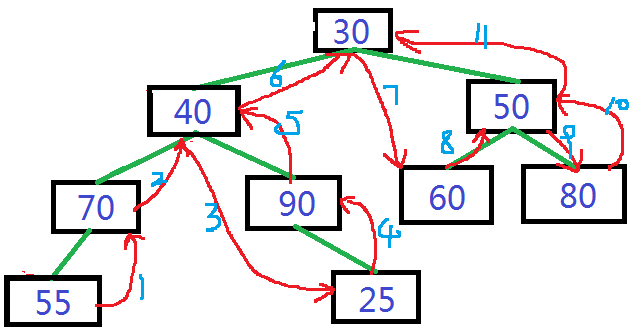
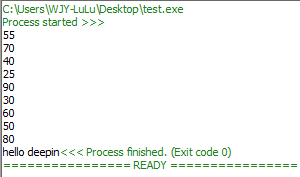
3.后续遍历

 #include <iostream>
 using namespace std;
 typedef int DATA;

 //建立二叉树的简单结构
 typedef struct SNode
 {
     DATA data;
     SNode *pLeft,*pRight;
     SNode(DATA d):data(d)//构造函数为了初始化方便
     {
         pLeft  = NULL;
         pRight = NULL;
     }
 }SNode;
 SNode* m_pRoot = NULL;//如果不定义全局变量，就需要通过函数参数传递
 void AddData()
 {
     //第一层
     SNode* p  = new SNode();
     m_pRoot = p;
     //第二层
     m_pRoot->pLeft  = new SNode();
     m_pRoot->pRight = new SNode();
     //第三层
     m_pRoot->pLeft->pLeft   = new SNode();
     m_pRoot->pLeft->pRight  = new SNode();
     m_pRoot->pRight->pLeft  = new SNode();
     m_pRoot->pRight->pRight = new SNode();
     //第四层
     m_pRoot->pLeft->pLeft->pLeft  = new SNode();
     m_pRoot->pLeft->pRight->pLeft = new SNode();
 }
 //后序遍历
 void BPrint(SNode* pRoot)
 {
     if(!pRoot) return;
     if(pRoot->pLeft)
         BPrint(pRoot->pLeft);
     if(pRoot->pRight)
         BPrint(pRoot->pRight);
     //递归调用本函数实现打印
     cout<<pRoot->data<<endl;
 }
 int main(int argc,char*argv[])
 {
     AddData();
     BPrint(m_pRoot);
     cout<<"hello deepin";
     return ;

 }

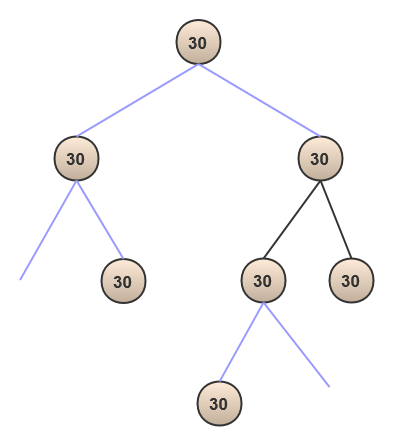
4.不知道啥树（貌似霍夫曼树）

　　遵循一个原则，添加的值大于某个节点，那么就在该节点左边添加，小于就在右边添加！

 #include <iostream>
 using namespace std;
 typedef int DATA;

 //建立二叉树的简单结构
 typedef struct SNode
 {
     DATA data;
     SNode *pLeft,*pRight;
     SNode(DATA d):data(d)//构造函数为了初始化方便
     {
         pLeft  = pRight = NULL;
     }
 }SNode;
 SNode* m_pRoot = NULL;//如果不定义全局变量，就需要通过函数参数传递
 void SetData(DATA data,SNode* &pRoot)
 {
     if(!pRoot)
     {
         SNode* p = new SNode(data);
         pRoot = p;
         return;
     }
        if(data <= pRoot->data)
         SetData(data,pRoot->pLeft);
     else
         SetData(data,pRoot->pRight);
 }
 //前序遍历
 void FPrint(SNode* pRoot)
 {
     if(!pRoot) return;
     cout<<pRoot->data<<endl;
     //递归调用本函数实现打印
     if(pRoot->pLeft)
         FPrint(pRoot->pLeft);
     if(pRoot->pRight)
         FPrint(pRoot->pRight);
 }
 int main(int argc,char*argv[])
 {
       SetData(,m_pRoot);
      SetData(,m_pRoot);
     SetData(,m_pRoot);
     SetData(,m_pRoot);
     SetData(,m_pRoot);
     SetData(,m_pRoot);
     SetData(,m_pRoot);
     FPrint(m_pRoot);
     cout<<"hello deepin";
     return ;
 }

https://chuanke.baidu.com/v1760453-135963-552446.html