监督学习——决策树理论与实践（下）：回归决策树（CART）

介绍

决策树分为分类决策树和回归决策树：

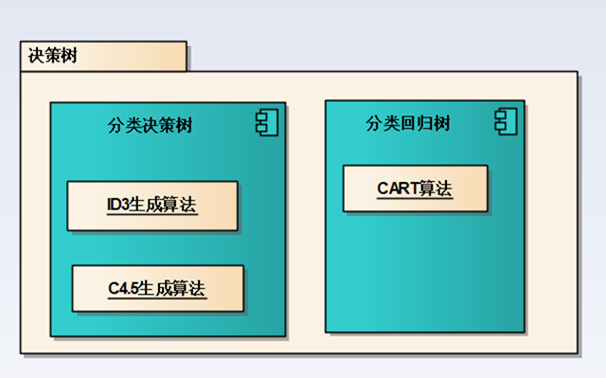
上一篇介绍了分类决策树以及Python实现分类决策树： 监督学习——决策树理论与实践（上）：分类决策树

         决策树是一种依托决策而建立起来的一种树。在机器学习中，决策树是一种预测模型，代表的是一种对象属性与对象值之间的一种映射关系，每一个节点代表某个对象/分类，树中的每一个分叉路径代表某个可能的属性值，而每一个叶子节点则对应从根节点到该叶子节点所经历的路径所表示的对象的值

通过训练数据构建决策树，可以高效的对未知的数据进行分类。决策数有两大优点：1）决策树模型可以读性好，具有描述性，有助于人工分析；2）效率高，决策树只需要一次构建，反复使用，每一次预测的最大计算次数不超过决策树的深度。

决策树是一颗树形的数据结构，可以是多叉树也可以是二叉树，决策树实际上是一种基于贪心策略构造的，每次选择的都是最优的属性进行分裂。

决策树也是一种监督学习算法，它的样本是（x,y）形式的输入输出样例。

回归树：

相对于上一篇所讲的决策树，这篇所讲的回归树主要解决回归问题，所以给定的训练数据输入和标签都是连续的。

---

CART回归树生成算法

决策树的生成

CART算法的思路是将特征空间切分为m个不同的子空间，通过测试数据（落在每个子空间中的测试数据）来计算每个子空间的输出值（对应下式中的Cm）。当这样的空间几何生成之后就可以很方便的将一个未知数据映射到某一个子空间Ri中，将Ci的值作为该未知数据的输出值。

这里Cm的取值一般采用均值算法，即取所有落在该子空间的测试数据的均作为该子空间的值：

这里肯定会涉及到一个，这也是CART算法的关键： 如何去划分一个一个子空间？如何去选择第j个变量Xj和它取值s作为切分变量和切分点，并定义成两个区域。这里《统计学方法》中给出了算法思路：

算法实现时，比那里所有切分向量，切分点是测试数据在Xj上的所有取值集合。通过5.19就能计算出当前最佳的切分向量j和切分点x以及划分成的两个区域的取值c1，c2。（该部分的Python实现对应下文中chooseBestSplit函数）

当对一个整体测试数据调用上面逻辑后会得到一个j和x值，通过这两个值将空间分成了两个空间，再分别对两个子空间调用上面的逻辑，这样递归下去就能生成一棵决策树。（对应下文中createTree函数）

决策树的剪枝

CART剪枝算法从“完全生长”的决策树的底端减去一些子树，使决策树变小（模型变简单），从而能够对未知数据有更准确的预测。

后续待补充

---

CART算法Python实现

数据加载

加载测试数据，以及测试数据的值（X,Y），这里数据和值都存放在一个矩阵中。

def loadDataSet(fileName):      #general function to parse tab -delimited floats
    dataMat = []                #assume last column is target value
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = map(float,curLine) #map all elements to float()
        dataMat.append(fltLine)
    return dataMat

数据划分

该函数用于切分数据集，将测试数据某一列中的元素大于和小于的测试数据分开，分别放到两个矩阵中：

def binSplitDataSet(dataSet, feature, value):
    mat0 = dataSet[nonzero(dataSet[:,feature] > value)[0],:][0]
    mat1 = dataSet[nonzero(dataSet[:,feature] <= value)[0],:][0]
    return mat0,mat1

输入参数 feature 为指定的某一列

value为切分点的值，通过该该值将dataset一份为二

寻找最优切分特征以及切分点

这里涉及到三个函数，分别在代码注释中进行了说明，真正计算最优值的函数为最后一个。

# 叶节点值计算函数： 这里以均值作为叶节点值
def regLeaf(dataSet):#returns the value used for each leaf
    return mean(dataSet[:,-1])

# 预测误差计算函数：这里用均方差表示
def regErr(dataSet):
    return var(dataSet[:,-1]) * shape(dataSet)[0]

# 遍历每一列中每个value值，找到最适合分裂的列和切分点
def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
    tolS = ops[0];   # 均方差最小优化值，如果大于该值则没有必要切分
    tolN = ops[1]    # 需要切分数据的最小长度，如果已经小于该值，则无需再切分
    #if all the target variables are the same value: quit and return value
    if len(set(dataSet[:,-1].T.tolist()[0])) == 1: #exit cond 1
        return None, leafType(dataSet)
    m,n = shape(dataSet)
    #the choice of the best feature is driven by Reduction in RSS error from mean
    S = errType(dataSet)
    bestS = inf; bestIndex = 0; bestValue = 0
    for featIndex in range(n-1):
        for splitVal in set(dataSet[:,featIndex]):
            mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
            if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN): continue
            newS = errType(mat0) + errType(mat1)
            if newS < bestS:
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
    #if the decrease (S-bestS) is less than a threshold don't do the split
    if (S - bestS) < tolS:
        return None, leafType(dataSet) #exit cond 2
    mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN):  #exit cond 3
        return None, leafType(dataSet)
    return bestIndex,bestValue#returns the best feature to split on
                              #and the value used for that split

回归树的创建

在上面函数基础之上，创建一个回归树也就不难了：

def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):#assume dataSet is NumPy Mat so we can array filtering
    feat, val = chooseBestSplit(dataSet, leafType, errType, ops)#choose the best split
    if feat == None: return val #if the splitting hit a stop condition return val
    retTree = {}
    retTree['spInd'] = feat
    retTree['spVal'] = val
    lSet, rSet = binSplitDataSet(dataSet, feat, val)
    retTree['left'] = createTree(lSet, leafType, errType, ops)
    retTree['right'] = createTree(rSet, leafType, errType, ops)
    return retTree

这里是一个递归调用，需要注意函数的终止条件，这里当数据集不能再分时才会触发终止条件，实际中这种操作很有可能会出现过拟合，可以认为地加一些终止条件进行“预剪枝”。

参考:

《机器学习实战》

《统计学习方法》

https://blog.csdn.net/u014568921/article/details/45082197