MATLAB一元线性回归分析

MATLAB一元线性回归分析应用举例

作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/

huigui.m

function [b,bint,r,rint,states,sima2,p,y0,zxqj]=huigui(x,y,x0)
%x –p元线性模型自变量的n个观测值的n×p矩阵，y -p元线性模型因变量的n个观测值的n×1向量，x0为预测值的横坐标
%b -模型系数β的最小二乘估计值，bint -模型系数β的100(1-alpha)%置信区间，r -模型拟合残差，rint -模型拟合残差的100(1-alpha)%置信区间.
%stats -包含R^2统计量、方差分析的F统计量的值、方差分析的显著性概率p值和sigama^2的估计值，y0为预测值纵坐标
format short;
x1=[ones(length(x),),x];
[b,bint,r,rint,states]=regress(y,x1);
sima2=(vpa(states(),));
p=vpa(states(),);   %检验的p值   p<0.01,回归方程高度显著;0.0.1<=p<0.05,回归方程显著;p>=0.05,回归方程不显著
y0=b()+b()*x0;
s=sqrt(states());
zxqj=[y0-*s,y0+*s];   %置信区间
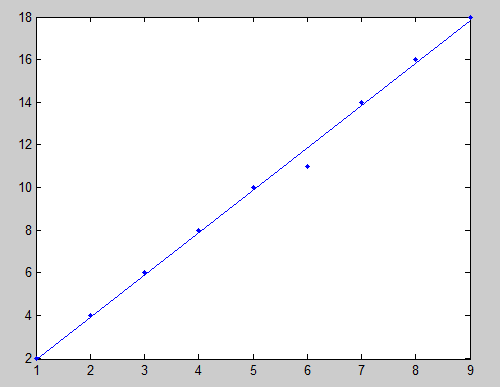
plot(x,y,'.'),lsline
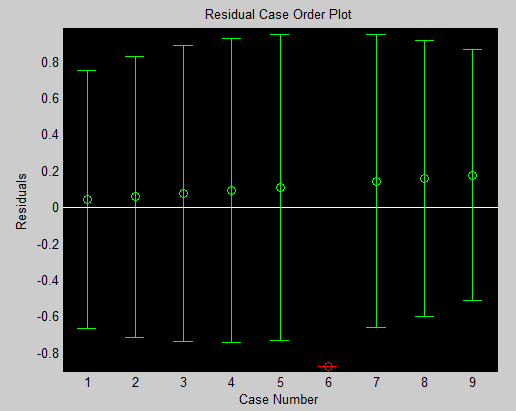
%rcoplot(r,rint)   %残差分析

结果：

>> x=[,,,,,,,,]';
>> y=[,,,,,,,,]';
>> x0=;
>> [b,bint,r,rint,states,sima2,p,y0,zxqj]=huigui(x,y,x0)

b =

   -0.0278
    1.9833

bint =

   -0.6342    0.5786
    1.8756    2.0911

r =

    0.0444
    0.0611
    0.0778
    0.0944
    0.1111
   -0.8722
    0.1444
    0.1611
    0.1778

rint =

   -0.6654    0.7543
   -0.7116    0.8338
   -0.7363    0.8918
   -0.7426    0.9315
   -0.7321    0.9543
   -0.8722   -0.8722
   -0.6611    0.9500
   -0.5981    0.9203
   -0.5124    0.8679

states =

   1.0e+03 *

    0.0010    1.8941    0.0000    0.0001

sima2 =

0.12460317460317460317

p =

0.00000000088276169535500757861

y0 =

   19.8056

zxqj =

   19.0996   20.5115

残差图：