Good Bye 2018 B. New Year and the Treasure Geolocation

传送门

https://www.cnblogs.com/violet-acmer/p/10201535.html

题意：

　　在二维空间中有 n 个 obelisk 点，n 个 p 点；

　　存在坐标T(x,y)，obelisk 中的每个点 o[ i ] : (x,y) 都可以在 p 中找到一个点 p[ j ] : (x,y) 使得 o[ i ].x + p[ j ].x == T.x , o[ i ].y + p[ j ].y == T.y ;

　　求出这个T点坐标。

题解：

　　我的做法--暴力枚举

　　让 o[1]点与每个 p[ i ] 点结合，假设 T( o[ 1 ].x + p[ j ].x , o[ 1 ].y + p[ j ].y ) ;

　　判断其余的o点能否找到某个p点，使得其坐标和为T( )，如果全部找到，输出T点坐标，否则，枚举下一个点；

AC代码：

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 using namespace std;
 #define mem(a,b) memset(a,b,sizeof(a))
 const int maxn=1e3+;

 int n;
 struct Node
 {
     int x,y;
 }o[maxn];
 struct Node1
 {
     int x,y;
 }p[maxn];
 bool vis[maxn];

 bool cmp(Node1 _a,Node1 _b)
 {
     return _a.x < _b.x;
 }
 bool Find(int x,int y)//判断p中有无点(x,y)
 {
     for(int i=;i <= n;++i)
         if(p[i].x == x && p[i].y == y)
             return true;
     return false;
 }
 void Solve()
 {
     sort(p+,p+n+,cmp);
     for(int i=;i <= n;++i)
     {
         int tX=o[].x+p[i].x;
         int tY=o[].y+p[i].y;
         bool flag=false;
         for(int j=;j <= n;++j)
             if(!Find(tX-o[j].x,tY-o[j].y))
                 flag=true;

         if(!flag)
         {
             printf("%d %d\n",tX,tY);
             return ;
         }
     }
 }
 int main()
 {
     scanf("%d",&n);
     for(int i=;i <= n;++i)
         scanf("%d%d",&o[i].x,&o[i].y);
     for(int i=;i <= n;++i)
         scanf("%d%d",&p[i].x,&p[i].y);
     Solve();
     return ;
 }

枚举

　　当时做的时候，就分析了一下时间复杂度O(n³)，又看了一下数据范围 n <= 1000，emmmm，可以过

　　赛后分析：

　　　　其实，当时还想着用二分来着（查找p中是否含有对应的(x,y)），因为看到了所有的x_i != x_j , y_i != y_j，但是比赛的时候并没有写，因为遍历一遍p数组比二分要容易好多。

　　　　然后，今天撸了一发二分的代码，wa，又看了一遍题，发现漏了个条件 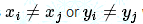 ，两坐标不等是用 or 连接的，而不是 and..........

　　　　又换了个查找方法，嵌套map

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<map>
 using namespace std;
 #define P pair<int ,int >
 const int maxn=1e3+;

 int n;
 P o[maxn];
 P p[maxn];
 map<int ,map<int ,bool> >mymap;//mymap[i][j] = true : p中含有点(x,y)

 void Solve()
 {
     for(int i=;i <= n;++i)
     {
         bool flag=false;
         P T=P(o[].first+p[i].first,o[].second+p[i].second);
         for(int j=;j <= n;++j)
         {
             int x=T.first-o[j].first;
             int y=T.second-o[j].second;
             if(mymap[x][y] == false)
                 flag=true;
         }
         if(!flag)
         {
             printf("%d %d\n",T.first,T.second);
             return ;
         }
     }
 }
 int main()
 {
 //    freopen("C:\\Users\\lenovo\\Desktop\\in.txt\\cf1091.txt","r",stdin);
     scanf("%d",&n);
     for(int i=;i <= n;++i)
     {
         int x,y;
         scanf("%d%d",&x,&y);
         o[i]=P(x,y);
     }
     for(int i=;i <= n;++i)
     {
         int x,y;
         scanf("%d%d",&x,&y);
         p[i]=P(x,y);
         mymap[x][y]=true;
     }
     Solve();
     return ;
 }

嵌套map查找是否含有相应的p坐标

　　　　上网搜了一下map的时间复杂度，emmmm，log(n);

　　　　然后，分析了一波代码时间复杂度,O(n²*log(n) );

　　　　那么，起不要比O(n³)快，提交一发看看，然鹅.......

　　　　莫非，嵌套map的时间复杂度不是log(n)???????