【C/C++】实现龙贝格算法

1. 复化梯形法公式以及递推化

复化梯形法是一种有效改善求积公式精度的方法。将[a,b]区间n等分，步长h = (b-a)/n，分点x_k = a + kh。复化求积公式就是将这n等分的每一个小区间进行常规的梯形法求积，再将这n的小区间累加求和。 公式如下：

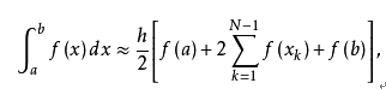
使用复化梯形法积分时，可以将此过程递推化，以更方便的使用计算机实现。设积分区间[a,b]，将此区间n等分，则等分点共有n+1个，使用复化梯形积分求得T_n。进行二分，二分结果记为T_2n，则有：

2. 龙贝格积分公式

龙贝格积分实际上是提高收敛速度的一种算法。由于复化梯形法步长减半后误差减少至 ，即有：

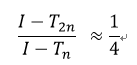
整理得：

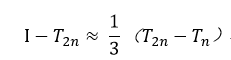
根据此思路，将收敛缓慢的梯形值序列Tn加工成收敛迅速的龙贝格值序列Rn，这就是龙贝格算法，加工算法流程如下：

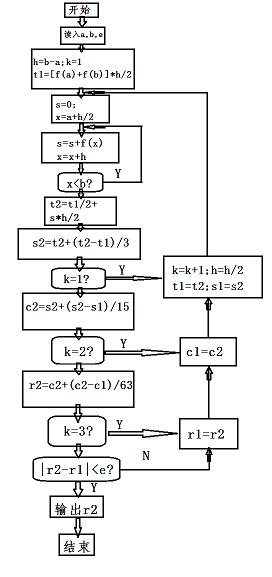
实现：

 #include<stdio.h>
 #include<math.h>
 #include<iostream>
 #include<cstdio>
 using namespace std;
 int Rk=;
 int Tk=;
 double fx(double x)   //被积函数
 {
     //if(x==0.0)return 1.0;
     return *x*x*x+*x*x+ + sin(x);
 }
 double getReal(double a,double b){
     double r1 = 3.0/4.0 * b*b*b*b + 2.0/3.0*b*b*b + b - cos(b);
     double r2 = 3.0/4.0 * a*a*a*a + 2.0/3.0*a*a*a + a - cos(a);
     return r1 - r2;
 }
 double getS(double a,double b,double h)
 {
     double res=0.0;
     for(double i=a+h/2.0; i<b; i+=h){
         res+=fx(i);
     }

     return res;
 }
 double Romberg(double a,double b,double e)
 {
     int k=;
     double T1,T2,S1,S2,C1,C2,R1,R2;
     double h=b-a;
     double s;
     T1=(fx(a)+fx(b))*h/2.0;
     int counter=;
     while()
     {
         Rk++;
         counter++;
         s=getS(a,b,h);
         T2=(T1+h*s)/2.0;
         S2=(4.0*T2-T1)/3.0;
         h/=2.0;
         T1=T2;
         S1=S2;
         C1=C2;
         R1=R2;
         if(k==)
         {
             k++;
             continue;
         }
         C2=(16.0*S2-S1)/15.0;
         if(k==)
         {
             k++;
             continue;
         }
         R2=(64.0*C2-C1)/63.0;
         if(k==)
         {
             k++;
             continue;
         }
         if(fabs(R1-R2)<e||counter>=)break;
     }
     return R2;
 }
 double Tn(double a,double b,double e)
 {
     double T1,T2;
     double h=b-a;
     T1=(fx(a)+fx(b))*h/2.0;
     while()
     {
         Tk++;
         double s=getS(a,b,h);
         T2=(T1+h*s)/2.0;
         if(fabs(T2-T1)<e)break;
         h/=2.0;
         T1=T2;
     }
     return T2;
 }
 int main()
 {
     double a,b,e;
     printf("输入积分限和精度： a b e:");
     //输入区间[a,b],和精度e
     scanf("%lf%lf%lf",&a,&b,&e);
     double t=Romberg(a,b,e);
     //分别输出龙贝格算法和梯形法的计算结果和相应二分次数
     printf("\nRomberg:积分值：%.7lf  --  二分次数：%d\n",t,Rk);
     t=Tn(a,b,e);
     printf("     Tn:积分值：%.7lf  --  二分次数：%d\n",t,Tk);
     double tf = getReal(a,b);
     printf("    Real:%.7lf",tf);
     return ;
 }