（四）java对象的结构和对象的访问定位

在HotSpot虚拟机中，对象在内存中存储的布局可以分为3块区域：对象头（Header）、实例数据（Instance Data）和对齐填充（Padding）。

一、 对象头

HotSpot虚拟机的对象头包括两部分信息：

• 第一部分markword,用于存储对象自身的运行时数据，如哈希码（HashCode）、GC分代年龄、锁状态标志、线程持有的锁、偏向线程ID、偏向时间戳等，这部分数据的长度在32位和64位的虚拟机（未开启压缩指针）中分别为32bit和64bit，官方称它为“MarkWord”。

• 另一部分是class对象指针，类型指针，即对象指向它的类元数据的指针，虚拟机通过这个指针来确定这个对象是哪个类的实例.

二、   实例数据

实例数据部分是对象真正存储的有效信息，也是在程序代码中所定义的各种类型的字段内容。无论是从父类继承下来的，还是在子类中定义的，都需要记录起来。

三、对齐填充

第三部分对齐填充并不是必然存在的，也没有特别的含义，它仅仅起着占位符的作用。由于HotSpot VM的自动内存管理系统要求对象起始地址必须是8字节的整数倍，换句话说，就是对象的大小必须是8字节的整数倍。而对象头部分正好是8字节的倍数（1倍或者2倍），因此，当对象实例数据部分没有对齐时，就需要通过对齐填充来补全。

四、对象大小计算

• 在32位系统下，存放Class指针的空间大小是4字节，MarkWord是4字节，对象头为8字节。

• 在64位系统下，存放Class指针的空间大小是8字节，MarkWord是8字节，对象头为16字节。

• 64位开启指针压缩的情况下，存放Class指针的空间大小是4字节，MarkWord是8字节，对象头为12字节。

• 数组长度4字节+数组对象头8字节(对象引用4字节（未开启指针压缩的64位为8字节）+数组markword为4字节（64位未开启指针压缩的为8字节）)+对齐4=16字节。

• 静态属性不算在对象大小内。

五、对象的访问定位

对象的访问定位  

建立对象是为了使用对象，我们的Java程序需要通过栈上的reference数据来操作堆上的具体对象。由于在Java虚拟机规范里面只规定了
reference类型 
是一个指向对象的引用，并没有定义这个引用应该通过什么种方式去定位、访问到堆中的对象的具体位置，对象访问方式也是取决于虚拟机实现而定的。主流的访问方式有使用句柄和直接指针两种。 


如果使用句柄访问的话，Java堆中将会划分出一块内存来作为句柄池，reference中存储的就是对象的句柄地址，而句柄中包含了对象实例数据与类型数据的具体各自的地址信息。如图1所示。

 



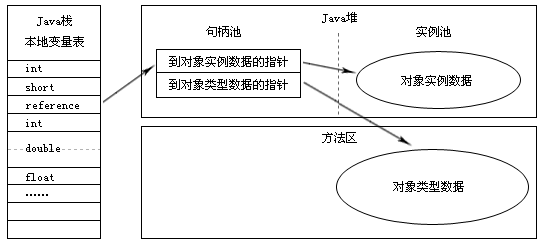
图1 通过句柄访问对象

如果使用直接指针访问的话，Java堆对象的布局中就必须考虑如何放置访问类型数据的相关信息，reference中存储的直接就是对象地址，如图2所示。

 


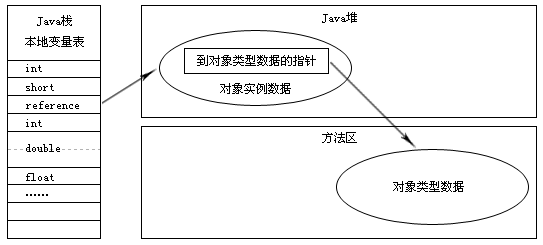
图2 通过直接指针访问对象

这两种对象访问方式各有优势，使用句柄来访问的最大好处就是reference中存储的是稳定句柄地址，在对象被移动（垃圾收集时移动对象是非常普遍的行为）时只会改变句柄中的实例数据指针，而reference本身不需要被修改。

使用直接指针来访问最大的好处就是速度更快，它节省了一次指针定位的时间开销，由于对象访问的在Java中非常频繁，因此这类开销积小成多也是一项非常可
观的执行成本。从上一部分讲解的对象内存布局可以看出，就虚拟机HotSpot而言，它是使用第二种方式进行对象访问，但在整个软件开发的范围来看，各种
语言、框架中使用句柄来访问的情况也十分常见。