hdu 6088 Rikka with Rock-paper-scissors (2017 多校第五场 1004） 【组合数学 + 数论 + 模意义下的FFT】

题目链接

首先利用组合数学知识，枚举两人的总胜场数容易得到

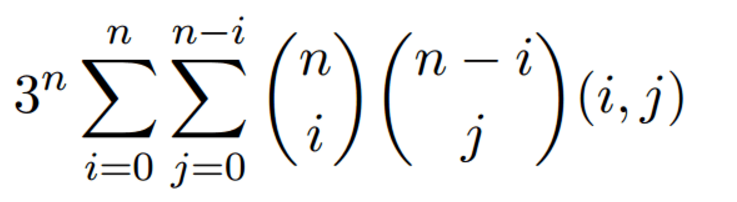
这还不是卷积的形式，直接搞的话复杂度大概是O(n^2)的，肯定会TLE。但似乎和卷积有点像？想半天没想出来。。多谢Q巨提醒，才知道可以用下面这个公式进行转化

最后，化得的公式为

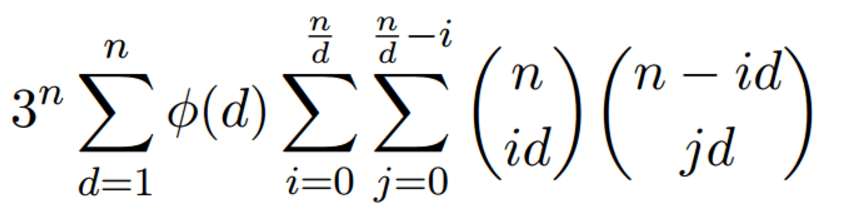
另外注意，上式右边是一个卷积的形式，但是，所得和的第一项是不需要加上的（不过图中公式没有体现）。结合实际意义大概就是，i==0&&j==0时，gcd(i,j)不存在约数d，虽然0可以被任意正整数整除 & 第一项不为0

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef double db;
#define upmo(a,b) (((a)=((a)+(b))%mod)<0?(a)+=mod:(a))    // 相加后取模 

int n,mod;

namespace FFT_MO    //前面需要有 mod(1e8~1e9级别),upmo(a,b) 的定义
{
    const int FFT_MAXN=<<;
    const db pi=.14159265358979323846264338327950288L;
    struct cp
    {
        db a,b;
        cp(double a_=,double b_=)
        {
            a=a_,b=b_;
        }
        cp operator +(const cp&rhs)const
        {
            return cp(a+rhs.a,b+rhs.b);
        }
        cp operator -(const cp&rhs)const
        {
            return cp(a-rhs.a,b-rhs.b);
        }
        cp operator *(const cp&rhs)const
        {
            return cp(a*rhs.a-b*rhs.b,a*rhs.b+b*rhs.a);
        }
        cp operator !()const
        {
            return cp(a,-b);
        }
    }nw[FFT_MAXN+],f[FFT_MAXN],g[FFT_MAXN],t[FFT_MAXN];    //a<->f,b<->g,t<~>c
    int bitrev[FFT_MAXN]; 

    void fft_init()    //初始化 nw[],bitrev[]
    {
        int L=;while((<<L)!=FFT_MAXN) L++;
        for(int i=;i<FFT_MAXN;i++)  bitrev[i]=bitrev[i>>]>>|((i&)<<(L-));
        for(int i=;i<=FFT_MAXN;i++) nw[i]=cp((db)cosl(*pi/FFT_MAXN*i),(db)sinl(*pi/FFT_MAXN*i));
    }

    // n已保证是2的整数次幂
    // flag=1:DFT |  flag=-1: IDFT
    void dft(cp *a,int n,int flag=)
    {
        int d=;while((<<d)*n!=FFT_MAXN) d++;
        for(int i=;i<n;i++) if(i<(bitrev[i]>>d))
            swap(a[i],a[bitrev[i]>>d]);    //    NOTICE!
        for(int l=;l<=n;l<<=)
        {
            int del=FFT_MAXN/l*flag;    // 决定 wn是在复平面是顺时针还是逆时针变化，以及变化间距
            for(int i=;i<n;i+=l) // ?????????????????
            {
                cp *le=a+i,*ri=a+i+(l>>);    // ?????????????????
                cp *w=flag==? nw:nw+FFT_MAXN;    // 确定wn的起点
                for(int k=;k<(l>>);k++)
                {
                    cp ne=*ri * *w;
                    *ri=*le-ne,*le=*le+ne;
                    le++,ri++,w+=del;
                }
            }
        }
        if(flag!=) for(int i=;i<n;i++) a[i].a/=n,a[i].b/=n;
    }

    // convo(a,n,b,m,c) a[0..n]*b[0..m] -> c[0..n+m]
    void convo(LL *a,int n,LL *b,int m,LL *c)
    {
        for(int i=;i<=n+m;i++) c[i]=;
        int N=;while(N<=n+m) N<<=;    // N是c扩展后的长度
        for(int i=;i<N;i++)    //扩展 a[],b[] ，存入f[],g[]，注意取模
        {
            LL aa=i<=n?a[i]:,bb=i<=m? b[i]:;
            aa%=mod,bb%=mod;
            f[i]=cp(db(aa>>),db(aa&));
            g[i]=cp(db(bb>>),db(bb&));
        }
        dft(f,N),dft(g,N);
        for(int i=;i<N;i++)    // 频域求积 // ?????????????????
        {
            int j=i? N-i:;
            t[i]=((f[i]+!f[j])*(!g[j]-g[i])+(!f[j]-f[i])*(g[i]+!g[j]))*cp(,0.25);
        }
        dft(t,N,-);
        for(int i=;i<=n+m;i++)    upmo(c[i],(LL(t[i].a+0.5))%mod<<);
        for(int i=;i<N;i++)    // 频域求积 // ?????????????????
        {
            int j=i? N-i:;
            t[i]=(!f[j]-f[i])*(!g[j]-g[i])*cp(-0.25,)+cp(,0.25)*(f[i]+!f[j])*(g[i]+!g[j]);
        }
        dft(t,N,-);
        for(int i=;i<=n+m;i++)    upmo(c[i],LL(t[i].a+0.5)+(LL(t[i].b+0.5)%mod<<));
    }
}

//==============预处理阶乘及阶乘逆元============== 

LL qpow(LL x,LL n)        //求x^n%mod
{
    LL ret=;
    for(; n; n>>=)
    {
        if(n&) ret=ret*x%mod;
        x=x*x%mod;
    }
    return ret;
}
LL inv(LL x)
{
    return qpow(x,mod-);
}
const LL M=1e5+;
LL fac[M+];            //阶乘
LL inv_of_fac[M+];        //阶乘的逆元
void init_fac()
{
    fac[]=;
    for(int i=; i<=M; i++)
        fac[i]=fac[i-]*i%mod;
    inv_of_fac[M]=qpow(fac[M],mod-);
    for(int i=M-; i>=; i--)
        inv_of_fac[i]=inv_of_fac[i+]*(i+)%mod;
}
//================================================

//===================phi(x)打表===================

const int maxn=;
int phi[maxn+];
void init_phi()
{
    memset(phi,,sizeof(phi));  //初始化为0
    phi[]=;
    for(int i=; i<=maxn; i++)
    {
        if(!phi[i])     //当i是质数时
            for(int j=i; j<=maxn; j+=i)      //筛选所有因子为i的数
            {
                if(!phi[j]) phi[j]=j;       //若未赋值过，先初始化
                phi[j]=phi[j]/i*(i-);      //i是质因数(1-1/i)=(i-1)/i，先除再乘是为了防止越界。
            }
    }
}
//================================================

LL a[<<|],b[<<|],c[<<|];

int main()
{
    init_phi();FFT_MO::fft_init();

    //=============debug==============

//    int n,m;
//    mod=1e9+7;
//    while(cin>>n>>m)
//    {
//        for(int i=0;i<=n;i++)    cin>>a[i];
//        for(int i=0;i<=m;i++)    cin>>b[i];
//        FFT_MO::convo(a,n,b,m,c);
//        for(int i=0;i<=n+m;i++)
//            cout<<c[i]<<' ';
//        puts("");
//    }

    //================================
    int T;scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&mod);
        init_fac();
        LL ans=;
        for(int d=;d<=n;d++)
        {
            int N=n/d;
            for(int i=;i<=N;i++) a[i]=b[i]=inv_of_fac[i*d];
            FFT_MO::convo(a,N,b,N,c);
            LL temp=;
            for(int i=;i<=N;i++) temp=(temp+c[i]*inv_of_fac[n-i*d])%mod;
            ans=(ans+temp*phi[d])%mod;
        }
        ans=ans*fac[n]%mod*qpow(,n)%mod;
        printf("%lld\n",ans);
    }
}

关于模意义下的FFT