python实现查找算法

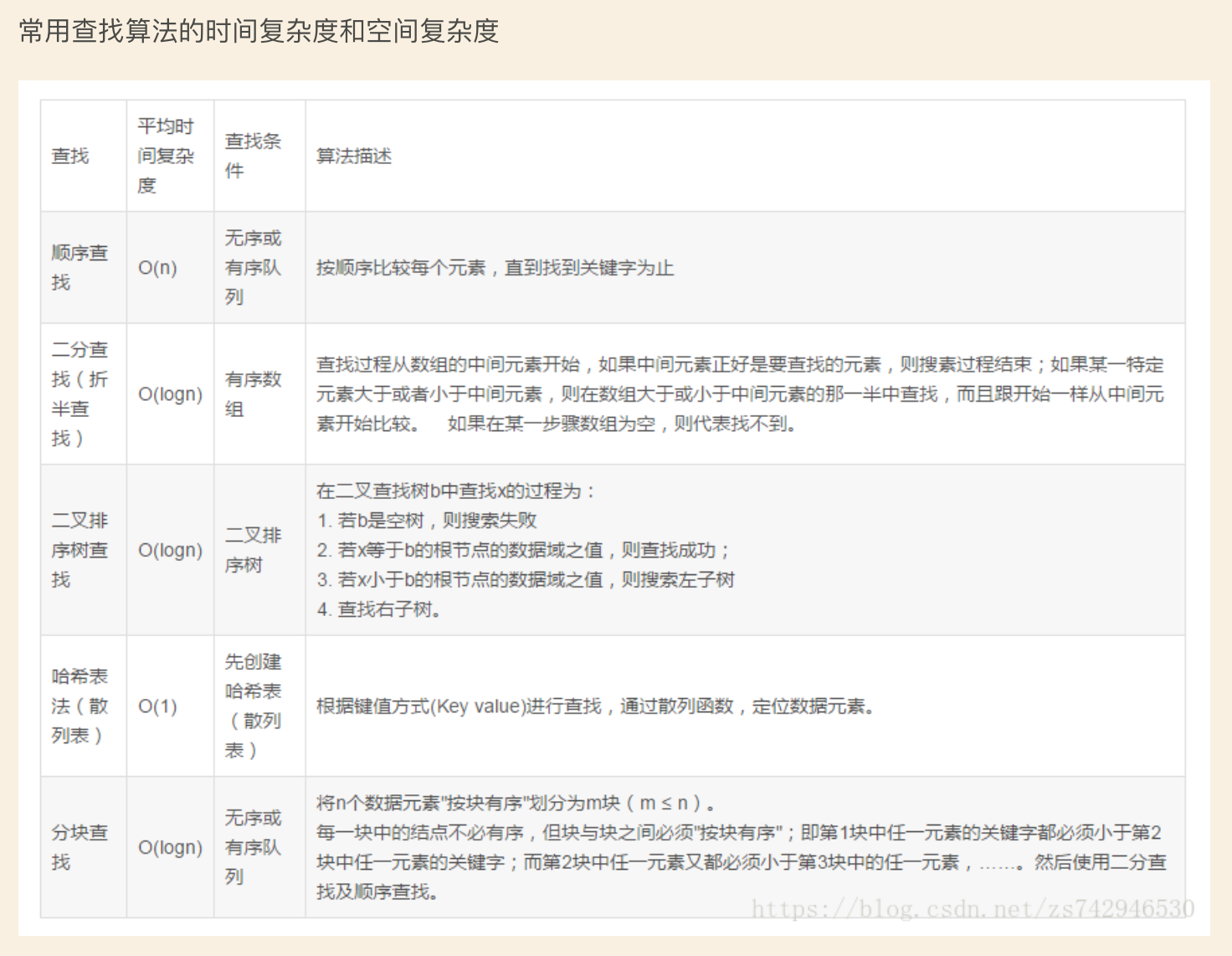
搜索是在一个项目集合中找到一个特定项目的算法过程。搜索通常的答案是真的或假的，因为该项目是否存在。 搜索的几种常见方法：顺序查找、二分法查找、二叉树查找、哈希查找

线性查找
线性查找就是从头找到尾，直到符合条件了就返回。比如在一个 list 中找到一个等于 5 的元素并返回下标：

number_list = [0, 1, 2, 3, 4, 5, 6, 7]

def linear_search(value, iterable):
    for index, val in enumerate(iterable):
        if val == value:
            return index
    return -1

assert linear_search(5, number_list) == 5

是不是 so easy。当然我们需要来一点花样，比如传一个谓词进去，你要知道，在 python 里一切皆对象，所以我们可以把函数当成一个参数传给另一个函数。

def linear_search_v2(predicate, iterable):
    for index, val in enumerate(iterable):
        if predicate(val):
            return index
return -1

assert linear_search_v2(lambda x: x == 5, number_list) == 5

效果是一样的，但是传入一个谓词函数进去更灵活一些，比如我们可以找到第一个大于或者小于 5 的，从而控制函数的行为。 还能玩出什么花样呢？前面我们刚学习了递归，能不能发挥自虐精神没事找事用递归来实现呢？

def linear_search_recusive(array, value):
    if len(array) == 0:
        return -1
        index = len(array)-1
    if array[index] == value:
        return index

return linear_search_recusive(array[0:index], value)

二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

二分法查找实现
（非递归实现）

def binary_search(alist, item):
    first = 0
    last = len(alist)-1
    while first<=last:
        midpoint = (first + last)/2
        if alist[midpoint] == item:
            return True
        elif item < alist[midpoint]:
            last = midpoint-1
        else:
            first = midpoint+1
            return False

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binary_search(testlist, 3))
print(binary_search(testlist, 13))

（递归实现）
def binary_search(alist, item):
    if len(alist) == 0:
        return False
    else:
        midpoint = len(alist)//2
    if alist[midpoint]==item:
        return True
    else:
        if item<alist[midpoint]:
        return binary_search(alist[:midpoint],item)
    else:
        return binary_search(alist[midpoint+1:],item)

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binary_search(testlist, 3))
print(binary_search(testlist, 13))er

时间复杂度

最优时间复杂度：O(1)
最坏时间复杂度：O(logn)

二叉树
二叉树的基本概念

二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）

二叉树的性质(特性)

性质1: 在二叉树的第i层上至多有2^(i-1)个结点（i>0）
性质2: 深度为k的二叉树至多有2^k - 1个结点（k>0）
性质3: 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1;
性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
性质5:对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2（i＝1 时为根,除外）

(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

二叉树的节点表示以及树的创建
通过使用Node类中定义三个属性，分别为elem本身的值，还有lchild左孩子和rchild右孩子

class Node(object):
    """节点类"""
    def __init__(self, elem=-1, lchild=None, rchild=None):
        self.elem = elem
        self.lchild = lchild
        self.rchild = rchild
    #树的创建,创建一个树的类，并给一个root根节点，一开始为空，随后添加节点

class Tree(object):
"""树类"""
    def __init__(self, root=None):
        self.root = root

    def add(self, elem):
    """为树添加节点"""
        node = Node(elem)
        #如果树是空的，则对根节点赋值
        if self.root == None:
            self.root = node
        else:
            queue = []
            queue.append(self.root)
        #对已有的节点进行层次遍历
        while queue:
        #弹出队列的第一个元素
            cur = queue.pop(0)
            if cur.lchild == None:
                cur.lchild = node
                return
            elif cur.rchild == None:
                cur.rchild = node
                return
            else:
            #如果左右子树都不为空，加入队列继续判断
                queue.append(cur.lchild)
                queue.append(cur.rchild)    

二叉树的遍历
树的遍历是树的一种重要的运算。所谓遍历是指对树中所有结点的信息的访问，即依次对树中每个结点访问一次且仅访问一次，我们把这种对所有节点的访问称为遍历（traversal）。那么树的两种重要的遍历模式是深度优先遍历和广度优先遍历,深度优先一般用递归，广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现。

深度优先遍历

对于一颗二叉树，深度优先搜索(Depth First Search)是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。
那么深度遍历有重要的三种方法。这三种方式常被用于访问树的节点，它们之间的不同在于访问每个节点的次序不同。这三种遍历分别叫做先序遍历（preorder），中序遍历（inorder）和后序遍历（postorder）。我们来给出它们的详细定义，然后举例看看它们的应用。

先序遍历 在先序遍历中，我们先访问根节点，然后递归使用先序遍历访问左子树，再递归使用先序遍历访问右子树
根节点->左子树->右子树

def preorder(self, root):
"""递归实现先序遍历"""
    if root == None:
        return
        print root.elem
    self.preorder(root.lchild)
    self.preorder(root.rchild)
中序遍历 在中序遍历中，我们递归使用中序遍历访问左子树，然后访问根节点，最后再递归使用中序遍历访问右子树
左子树->根节点->右子树

def inorder(self, root):
"""递归实现中序遍历"""
    if root == None:
        return
    self.inorder(root.lchild)
    print root.elem
    self.inorder(root.rchild)
后序遍历 在后序遍历中，我们先递归使用后序遍历访问左子树和右子树，最后访问根节点
左子树->右子树->根节点

def postorder(self, root):
"""递归实现后续遍历"""
    if root == None:
        return
    self.postorder(root.lchild)
    self.postorder(root.rchild)
    print root.elem

广度优先遍历(层次遍历)
从树的root开始，从上到下从从左到右遍历整个树的节点

def breadth_travel(self, root):
"""利用队列实现树的层次遍历"""
    if root == None:
        return
    queue = []
    queue.append(root)
    while queue:
        node = queue.pop(0)
    print node.elem,
    if node.lchild != None:
        queue.append(node.lchild)
    if node.rchild != None:
        queue.append(node.rchild)