(转)查找算法：二叉排序树(BSTree)

二叉排序树(Binary Sort Tree)，又称为二叉查找树(Binary Search Tree) ，即BSTree。

构造一棵二叉排序树的目的，其实并不是为了排序，而是为了提高查找和插入删除的效率。

什么是二叉排序树呢？二叉排序树具有以下几个特点。

（1）若根节点有左子树，则左子树的所有节点都比根节点小。

（2）若根节点有右子树，则右子树的所有节点都比根节点大。

（3）根节点的左，右子树也分别是二叉排序树。

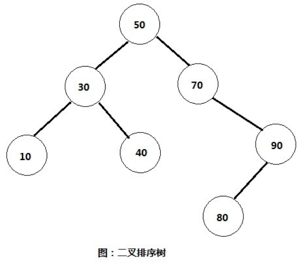
1、二叉排序树的图示

下面是二叉排序树的图示，通过它可以加深对二叉排序树的理解。

2、二叉排序树常见的操作及思路

下面是二叉排序树常见的操作及思路。

2-1、插入节点

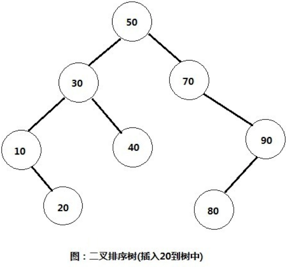
思路：比如我们要插入数字20到这棵二叉排序树中。那么步骤如下：

（1）首先将20与根节点进行比较，发现比根节点小，所以继续与根节点的左子树30比较。

（2）发现20比30也要小，所以继续与30的左子树10进行比较。

（3）发现20比10要大，所以就将20插入到10的右子树中。

此时的二叉排序树如下图：

2-2、查找节点

比如我们要查找节点10，那么思路如下：

（1）还是一样，首先将10与根节点50进行比较，发现比根节点要小，所以继续与根节点的左子树30进行比较。

（2）发现10比左子树30要小，所以继续与30的左子树10进行比较。

（3）发现两值相等，即查找成功，返回10的位置。

2-3、删除节点

删除节点的情况相对复杂，主要分为以下三种情形：

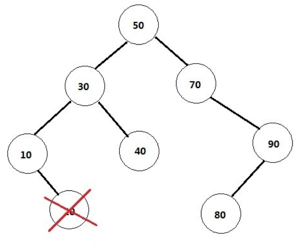
（1）删除的是叶节点(即没有孩子节点的)。比如20，删除它不会破坏原来树的结构，最简单。如图所示。

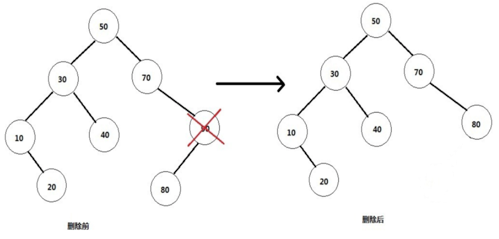
（2）删除的是单孩子节点。比如90，删除它后需要将它的孩子节点与自己的父节点相连。情形比第一种复杂一些。

（3）删除的是有左右孩子的节点。比如根节点50

这里有一个问题就是删除它后，谁将作为根节点？利用二叉树的中序遍历，就是右节点的左子树的最左孩子。

3、代码

有了思路之后，下面就开始写代码来实现这些功能。

BSTreeNode.java

public class BSTreeNode {
    public int data;
    public BSTreeNode left;
    public BSTreeNode right;

    public BSTreeNode(int data) {
        this.data = data;
    }
}

BSTreeOperate.java

/**
 * 二叉排序树的常见操作
 */
public class BSTreeOperate {

    // 树的根节点
    public BSTreeNode root;
    // 记录树的节点个数
    public int size;

    /**
     * 创建二叉排序树
     *
     * @param list
     * @return
     */
    public BSTreeNode create(int[] list) {

        for (int i = 0; i < list.length; i++) {
            insert(list[i]);
        }
        return root;
    }

    /**
     * 插入一个值为data的节点
     *
     * @param data
     */
    public void insert(int data) {
        insert(new BSTreeNode(data));
    }

    /**
     * 插入一个节点
     *
     * @param bsTreeNode
     */
    public void insert(BSTreeNode bsTreeNode) {
        if (root == null) {
            root = bsTreeNode;
            size++;
            return;
        }
        BSTreeNode current = root;
        while (true) {
            if (bsTreeNode.data <= current.data) {
                // 如果插入节点的值小于当前节点的值，说明应该插入到当前节点左子树，而此时如果左子树为空，就直接设置当前节点的左子树为插入节点。
                if (current.left == null) {
                    current.left = bsTreeNode;
                    size++;
                    return;
                }
                current = current.left;
            } else {
                // 如果插入节点的值大于当前节点的值，说明应该插入到当前节点右子树，而此时如果右子树为空，就直接设置当前节点的右子树为插入节点。
                if (current.right == null) {
                    current.right = bsTreeNode;
                    size++;
                    return;
                }
                current = current.right;
            }
        }
    }

    /**
     * 中序遍历
     *
     * @param bsTreeNode
     */
    public void LDR(BSTreeNode bsTreeNode) {
        if (bsTreeNode != null) {
            // 遍历左子树
            LDR(bsTreeNode.left);
            // 输出节点数据
            System.out.print(bsTreeNode.data + " ");
            // 遍历右子树
            LDR(bsTreeNode.right);
        }
    }

    /**
     * 查找节点
     */
    public boolean search(BSTreeNode bsTreeNode, int key) {
        // 遍历完没有找到，查找失败
        if (bsTreeNode == null) {
            return false;
        }
        // 要查找的元素为当前节点，查找成功
        if (key == bsTreeNode.data) {
            return true;
        }
        // 继续去当前节点的左子树中查找，否则去当前节点的右子树中查找
        if (key < bsTreeNode.data) {
            return search(bsTreeNode.left, key);
        } else {
            return search(bsTreeNode.right, key);
        }
    }
}

BSTreeOperateTest.java

public class BSTreeOperateTest {
    public static void main(String[] args) {
        BSTreeOperate bsTreeOperate = new BSTreeOperate();
        int[] list = new int[]{50, 30, 70, 10, 40, 90, 80};
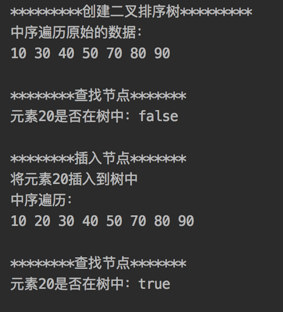
        System.out.println("*********创建二叉排序树*********");
        BSTreeNode bsTreeNode = bsTreeOperate.create(list);
        System.out.println("中序遍历原始的数据：");
        bsTreeOperate.LDR(bsTreeNode);
        System.out.println("");
        System.out.println("");

        System.out.println("********查找节点*******");
        System.out.println("元素20是否在树中：" + bsTreeOperate.search(bsTreeNode, 20));
        System.out.println("");

        System.out.println("********插入节点*******");
        System.out.println("将元素20插入到树中");
        bsTreeOperate.insert(20);
        System.out.println("中序遍历：");
        bsTreeOperate.LDR(bsTreeNode);
        System.out.println("");
        System.out.println("");

        System.out.println("********查找节点*******");
        System.out.println("元素20是否在树中：" + bsTreeOperate.search(bsTreeNode, 20));
        System.out.println("");
    }
}

运行结果：

欢迎转载，但请保留文章原始出处

本文地址：http://www.cnblogs.com/nnngu/p/8294714.html