【做题】atc_cf17-final_E - Combination Lock——巧妙转化及图论

题意：给出一个由26个小写字母组成的字符串，可以任意地进行若干个操作，每次操作是让指定区间内的字母变为下一个字母（z变成a）。问是否存在方案使得这个字符串变为回文串。

一开始的想法是构造len/2条模26意义下方程，但由于26不是质数，判断有没有解并不容易。（下文自动省略模26）

我们发现，一次操作对于方程组的影响大概是这样的：

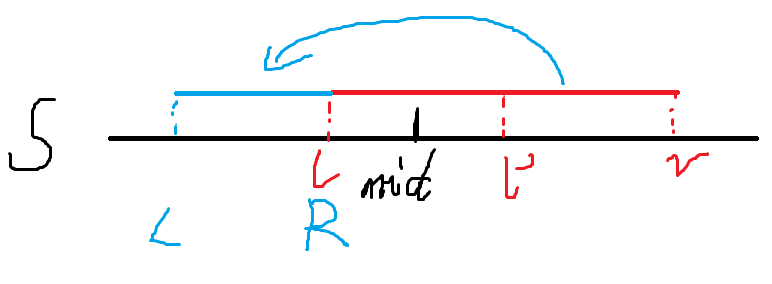
如上图所示，一次对区间[l,r]进行的操作，其中从一端到其关于中点的对称点的区间实质是没有贡献的。（上图中为区间[l,l']）同样地，对于完全位于中点右边的区间，可以将其翻转到中点左边。

因此，所有操作的影响都被移动到了中点左边，则每一条方程都变成了如下形式：k₁*x₁+k₂*x₂+...+k_n*x_n=p。其中，p为常数，且k_i为0或1。

而且，每一次操作的影响都是一个区间，所以这就成了一个通过区间操作是一个序列中元素全部变为0的问题。

上述问题简单地说就是，回文串就是左右两边的元素差值为0。所以最终目的就是使这些差值全部变为0。

所以很容易想到对于那个需要变成0的数列差分得到序列a，每一次操作区间[l,r]就是a[l]+1，a[r+1]-1。这等价于令a[l]+a[r+1]一定，然后任意确定a[l]和a[r+1]的值。

同样地，两个操作[l₁,r-1]和[l₂,r-1]也就是a[l₁]+a[l₂]+a[r]一定，然后任意确定这三个数的值。

因此，我们可以建一张有len/2+1个点的图，点i的权值为a[i]，每一次操作[l,r]就是给点l和点r+1连一条边。则存在方案 <=> 每个连通分量内点权和为0。

上述过程可以用并查集实现。

时间复杂度O(n*α(len))。（下面代码没有按秩合并，时间复杂度为O(n*logn)；有代码更优美的实现方式，即计算时保留S的右半部分）

 #include <bits/stdc++.h>
 using namespace std;
 const int N = ;
 int n,m,s[N],sum[N],dif[N];
 int flag[N];
 int get_flag(int pos) {
     return flag[pos] == pos ? pos : flag[pos] = get_flag(flag[pos]);
 }
 void fit(int& x) {
     if (x > n/) x = n-x+;
 }
 int fix(int x) {
     if (x<) x = -(-x)%;
     x %= ;
     return x;
 }
 int main() {
     int l,r;
     for (char tmp=getchar();tmp>='a'&&tmp<='z';tmp=getchar())
         s[++n] = tmp-'a';
     for (int i=;i<=n/;++i)
         s[i] -= s[n-i+],dif[i]=s[i]-s[i-],flag[i]=i;
     dif[n/+] = -s[n/];
     scanf("%d",&m);
     for (int i=;i<=m;++i) {
         scanf("%d%d",&l,&r);
         if (n&) {
             if (l == n/+&&r == n/+) continue;
             if (l == n/+) l++;
             if (r == n/+) r--;
         }
         if (l<=n/&&r>n/) {
             fit(r);
             if (l>r) swap(l,r);
             r--;
         } else {
             fit(l);fit(r);
             if (l>r) swap(l,r);
         }
         flag[get_flag(l)]=flag[get_flag(r+)];
     }
     for (int i=;i<=n/+;++i) sum[get_flag(i)] += dif[i];
     for (int i=;i<=n/+;++i) if (fix(sum[i])!=) {
         return *puts("NO");
     }
     puts("YES");
     return ;
 }

小结：一种重要解题方法就是对题目进行转化。