数据结构和算法(Golang实现)(17)常见数据结构-树

树

树是一种比较高级的基础数据结构，由n个有限节点组成的具有层次关系的集合。

树的定义：

1. 有节点间的层次关系，分为父节点和子节点。
2. 有唯一一个根节点，该根节点没有父节点。
3. 除了根节点，每个节点有且只有一个父节点。
4. 每一个节点本身以及它的后代也是一棵树，是一个递归的结构。
5. 没有后代的节点称为叶子节点，没有节点的树称为空树。

二叉树：每个节点最多只有两个儿子节点的树。

满二叉树：叶子节点与叶子节点之间的高度差为0的二叉树，即整颗树是满的，树呈满三角形结构。在国外的定义，非叶子节点儿子都是满的树就是满二叉树。我们以国内为准。

完全二叉树：完全二叉树是由满二叉树而引出来的，设二叉树的深度为k，除第k层外，其他各层的节点数都达到最大值，且第k层所有的节点都连续集中在最左边。

树根据儿子节点的多寡，有二叉树，三叉树，四叉树等，我们这里主要介绍二叉树。

一、二叉树的数学特征

1. 高度为h≥0的二叉树至少有h+1个结点，比如最不平衡的二叉树就是退化的线性链表结构，所有的节点都只有左儿子节点，或者所有的节点都只有右儿子节点。
2. 高度为h≥0的二叉树至多有2^h+1个节点，比如这颗树是满二叉树。
3. 含有n≥1个结点的二叉树的高度至多为n-1，由1退化的线性链表可以反推。
4. 含有n≥1个结点的二叉树的高度至少为logn，由2满二叉树可以反推。
5. 在二叉树的第i层，至多有2^(i-1)个节点，比如该层是满的。

二、二叉树的实现

二叉树可以使用链表来实现。如下：

// 二叉树
type TreeNode struct {
    Data  string    // 节点用来存放数据
    Left  *TreeNode // 左子树
    Right *TreeNode // 右字树
}

当然，数组也可以用来表示二叉树，一般用来表示完全二叉树。

对于一颗有n个节点的完全二叉树，从上到下，从左到右进行序号编号，对于任一个节点，编号i=0表示树根节点，编号i的节点的左右儿子节点编号分别为：2i+1,2i+2，父亲节点编号为：i/2，整除操作去掉小数。

如图是一颗完全二叉树，数组的表示：

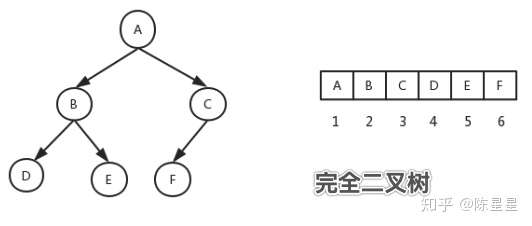
我们一般使用二叉树来实现查找的功能，所以树节点结构体里存放数据的Data字段。

三、遍历二叉树

构建一颗树后，我们希望遍历它，有四种遍历方法：

1. 先序遍历：先访问根节点，再访问左子树，最后访问右子树。
2. 后序遍历：先访问左子树，再访问右子树，最后访问根节点。
3. 中序遍历：先访问左子树，再访问根节点，最后访问右子树。
4. 层次遍历：每一层从左到右访问每一个节点。

先序，后序和中序遍历较简单，代码如下：

package main

import (
    "fmt"
)

// 二叉树
type TreeNode struct {
    Data  string    // 节点用来存放数据
    Left  *TreeNode // 左子树
    Right *TreeNode // 右字树
}

// 先序遍历
func PreOrder(tree *TreeNode) {
    if tree == nil {
        return
    }

    // 先打印根节点
    fmt.Print(tree.Data, " ")
    // 再打印左子树
    PreOrder(tree.Left)
    // 再打印右字树
    PreOrder(tree.Right)
}

// 中序遍历
func MidOrder(tree *TreeNode) {
    if tree == nil {
        return
    }

    // 先打印左子树
    MidOrder(tree.Left)
    // 再打印根节点
    fmt.Print(tree.Data, " ")
    // 再打印右字树
    MidOrder(tree.Right)
}

// 后序遍历
func PostOrder(tree *TreeNode) {
    if tree == nil {
        return
    }

    // 先打印左子树
    MidOrder(tree.Left)
    // 再打印右字树
    MidOrder(tree.Right)
    // 再打印根节点
    fmt.Print(tree.Data, " ")
}

func main() {
    t := &TreeNode{Data: "A"}
    t.Left = &TreeNode{Data: "B"}
    t.Right = &TreeNode{Data: "C"}
    t.Left.Left = &TreeNode{Data: "D"}
    t.Left.Right = &TreeNode{Data: "E"}
    t.Right.Left = &TreeNode{Data: "F"}

    fmt.Println("先序排序：")
    PreOrder(t)
    fmt.Println("\n中序排序：")
    MidOrder(t)
    fmt.Println("\n后序排序")
    PostOrder(t)
}

表示将以下结构的树进行遍历：

结果如下：

先序排序：
A B D E C F
中序排序：
D B E A F C
后序排序
D B E F C A

层次遍历较复杂，用到一种名叫广度遍历的方法，需要使用辅助的先进先出的队列。

1. 先将树的根节点放入队列。
2. 从队列里面remove出节点，先打印节点值，如果该节点有左子树节点，左子树入栈，如果有右子树节点，右子树入栈。
3. 重复2，直到队列里面没有元素。

核心逻辑如下：

func LayerOrder(treeNode *TreeNode) {
    if treeNode == nil {
        return
    }

    // 新建队列
    queue := new(LinkQueue)
    // 根节点先入队
    queue.Add(treeNode)
    for queue.size > 0 {
        // 不断出队列
        element := queue.Remove()

        // 先打印节点值
        fmt.Print(element.Data, " ")

        // 左子树非空，入队列
        if element.Left != nil {
            queue.Add(element.Left)
        }

        // 右子树非空，入队列
        if element.Right != nil {
            queue.Add(element.Right)
        }
    }
}

完整代码：

package main

import (
    "fmt"
    "sync"
)

// 二叉树
type TreeNode struct {
    Data  string    // 节点用来存放数据
    Left  *TreeNode // 左子树
    Right *TreeNode // 右字树
}

func LayerOrder(treeNode *TreeNode) {
    if treeNode == nil {
        return
    }

    // 新建队列
    queue := new(LinkQueue)

    // 根节点先入队
    queue.Add(treeNode)
    for queue.size > 0 {
        // 不断出队列
        element := queue.Remove()

        // 先打印节点值
        fmt.Print(element.Data, " ")

        // 左子树非空，入队列
        if element.Left != nil {
            queue.Add(element.Left)
        }

        // 右子树非空，入队列
        if element.Right != nil {
            queue.Add(element.Right)
        }
    }
}

// 链表节点
type LinkNode struct {
    Next  *LinkNode
    Value *TreeNode
}

// 链表队列，先进先出
type LinkQueue struct {
    root *LinkNode  // 链表起点
    size int        // 队列的元素数量
    lock sync.Mutex // 为了并发安全使用的锁
}

// 入队
func (queue *LinkQueue) Add(v *TreeNode) {
    queue.lock.Lock()
    defer queue.lock.Unlock()

    // 如果栈顶为空，那么增加节点
    if queue.root == nil {
        queue.root = new(LinkNode)
        queue.root.Value = v
    } else {
        // 否则新元素插入链表的末尾
        // 新节点
        newNode := new(LinkNode)
        newNode.Value = v

        // 一直遍历到链表尾部
        nowNode := queue.root
        for nowNode.Next != nil {
            nowNode = nowNode.Next
        }

        // 新节点放在链表尾部
        nowNode.Next = newNode
    }

    // 队中元素数量+1
    queue.size = queue.size + 1
}

// 出队
func (queue *LinkQueue) Remove() *TreeNode {
    queue.lock.Lock()
    defer queue.lock.Unlock()

    // 队中元素已空
    if queue.size == 0 {
        panic("over limit")
    }

    // 顶部元素要出队
    topNode := queue.root
    v := topNode.Value

    // 将顶部元素的后继链接链上
    queue.root = topNode.Next

    // 队中元素数量-1
    queue.size = queue.size - 1

    return v
}

// 队列中元素数量
func (queue *LinkQueue) Size() int {
    return queue.size
}

func main() {
    t := &TreeNode{Data: "A"}
    t.Left = &TreeNode{Data: "B"}
    t.Right = &TreeNode{Data: "C"}
    t.Left.Left = &TreeNode{Data: "D"}
    t.Left.Right = &TreeNode{Data: "E"}
    t.Right.Left = &TreeNode{Data: "F"}

    fmt.Println("\n层次排序")
    LayerOrder(t)
}

输出：

层次排序
A B C D E F

系列文章入口

我是陈星星，欢迎阅读我亲自写的 数据结构和算法(Golang实现)，文章首发于 阅读更友好的GitBook。

• 数据结构和算法(Golang实现)(1)简单入门Golang-前言
• 数据结构和算法(Golang实现)(2)简单入门Golang-包、变量和函数
• 数据结构和算法(Golang实现)(3)简单入门Golang-流程控制语句
• 数据结构和算法(Golang实现)(4)简单入门Golang-结构体和方法
• 数据结构和算法(Golang实现)(5)简单入门Golang-接口
• 数据结构和算法(Golang实现)(6)简单入门Golang-并发、协程和信道
• 数据结构和算法(Golang实现)(7)简单入门Golang-标准库
• 数据结构和算法(Golang实现)(8.1)基础知识-前言
• 数据结构和算法(Golang实现)(8.2)基础知识-分治法和递归
• 数据结构和算法(Golang实现)(9)基础知识-算法复杂度及渐进符号
• 数据结构和算法(Golang实现)(10)基础知识-算法复杂度主方法
• 数据结构和算法(Golang实现)(11)常见数据结构-前言
• 数据结构和算法(Golang实现)(12)常见数据结构-链表
• 数据结构和算法(Golang实现)(13)常见数据结构-可变长数组
• 数据结构和算法(Golang实现)(14)常见数据结构-栈和队列
• 数据结构和算法(Golang实现)(15)常见数据结构-列表
• 数据结构和算法(Golang实现)(16)常见数据结构-字典
• 数据结构和算法(Golang实现)(17)常见数据结构-树
• 数据结构和算法(Golang实现)(18)排序算法-前言
• 数据结构和算法(Golang实现)(19)排序算法-冒泡排序
• 数据结构和算法(Golang实现)(20)排序算法-选择排序
• 数据结构和算法(Golang实现)(21)排序算法-插入排序
• 数据结构和算法(Golang实现)(22)排序算法-希尔排序
• 数据结构和算法(Golang实现)(23)排序算法-归并排序
• 数据结构和算法(Golang实现)(24)排序算法-优先队列及堆排序
• 数据结构和算法(Golang实现)(25)排序算法-快速排序
• 数据结构和算法(Golang实现)(26)查找算法-哈希表
• 数据结构和算法(Golang实现)(27)查找算法-二叉查找树
• 数据结构和算法(Golang实现)(28)查找算法-AVL树
• 数据结构和算法(Golang实现)(29)查找算法-2-3树和左倾红黑树
• 数据结构和算法(Golang实现)(30)查找算法-2-3-4树和普通红黑树