KMP 知识点整理

1.扩展KMP

2.最大表示法

3.最小表示法

（扩展KMP）

hdu2594  模板题

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
using namespace std;
/*
* 扩展KMP算法
*/
//nxt[i]:x[i...m-1]与x[0...m-1]的最长公共前缀
//extend[i]:y[i...n-1]与x[0...m-1]的最长公共前缀
int nxt[];
int extend[];
char s[], t[];
void pre_EKMP(char x[],int m,int nxt[])
{
    nxt[]=m;
    int j=;
    while(j+<m && x[j]==x[j+]) j++;
    nxt[]=j;
    int k=;
    for(int i=;i<m;i++)
    {
        int p=nxt[k]+k-;
        int L=nxt[i-k];
        if(i+L<p+)nxt[i]=L;
        else
        {
            j=max(,p-i+);
            while(i+j<m && x[i+j]==x[j])j++;
            nxt[i]=j;
            k=i;
        }
    }
}
void EKMP(char x[],int m,char y[],int n,int nxt[],int extend[])
{
    pre_EKMP(x,m,nxt);
    int j=;
    while(j<n && j<m && x[j]==y[j]) j++;
    extend[]=j;
    int k=;
    for(int i=;i<n;i++)
    {
        int p=extend[k]+k-;
        int L=nxt[i-k];
        if(i+L<p+)
            extend[i]=L;
        else
        {
            j=max(,p-i+);
            while(i+j<n && j<m && y[i+j]==x[j]) j++;
            extend[i]=j;
            k=i;
        }
    }
}

int main()
{
    while(cin >> s >> t)
    {
        int slen = strlen(s),tlen = strlen(t);
        EKMP(s,slen,t,tlen,nxt,extend);
        int ans = ;

        for(int i = tlen - , j = ; j < slen; j++, i--)
        {
            if(extend[i] == tlen - i)
            {
                ans = max(ans, extend[i]);
            }
        }
        if(ans)
        {
            for(int i = ; i < ans; i++)
                cout << s[i];
            cout << " ";
        }
        cout << ans <<endl;
    }
    return ;
}

(最小表示法)

hdu2609

题目链接：
http://acm.hdu.edu.cn/showproblem.php?pid=2609

思路：
将每个字符串转换成最小串，然后放在set里面去重。

最小表示法：

循环字符串的最小表示法的问题可以这样描述：

对于一个字符串S，求S的循环的同构字符串S’中字典序最小的一个。

由于语言能力有限，还是用实际例子来解释比较容易：

设S=bcad，且S’是S的循环同构的串。S’可以是bcad或者cadb,adbc,dbca。而且最小表示的S’是adbc。

对于字符串循环同构的最小表示法，其问题实质是求S串的一个位置，从这个位置开始循环输出S，得到的S’字典序最小。

维护两个指针i,j。

令i=0,j=1

如果S[i] > S[j] i=j, j=i+1

如果S[i] < S[j] j++

如果S[i]==S[j] 设指针k，分别从i和j位置向下比较，直到S[i] != S[j]

如果S[i+k] > S[j+k] i=i+k

否则j++

返回i和j的小者

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <set>
#include <algorithm>
using namespace std;

const int N = ;
int n,len;
set<string> v;
char s[N], t[N];

int minRepresstation(char *s){
    int i = ,j = ,k = ;
    while(i<len && j<len && k<len){
        int tmp = s[(i+k)%len]-s[(j+k)%len];
        if(tmp == )
            k++;
        else{
            if(tmp > )
                i += k+;
            else
                j += k+;
            if(i == j)
                j++;
            k = ;
        }
    }
    return min(i,j);
}

void getMin(char* str) {
    str[len/] = '\0';
    v.insert (str);
}

int main(){
    while(~scanf("%d", &n)){
        v.clear();
        for(int i = ; i < n; i++){
            scanf("%s",t);
            strcpy(s,t);
            strcat(s,t);
            len = strlen(s);
            int k = minRepresstation(s);
            getMin(s+k);
        }
        printf("%d\n",v.size());
    }
    return ;
}

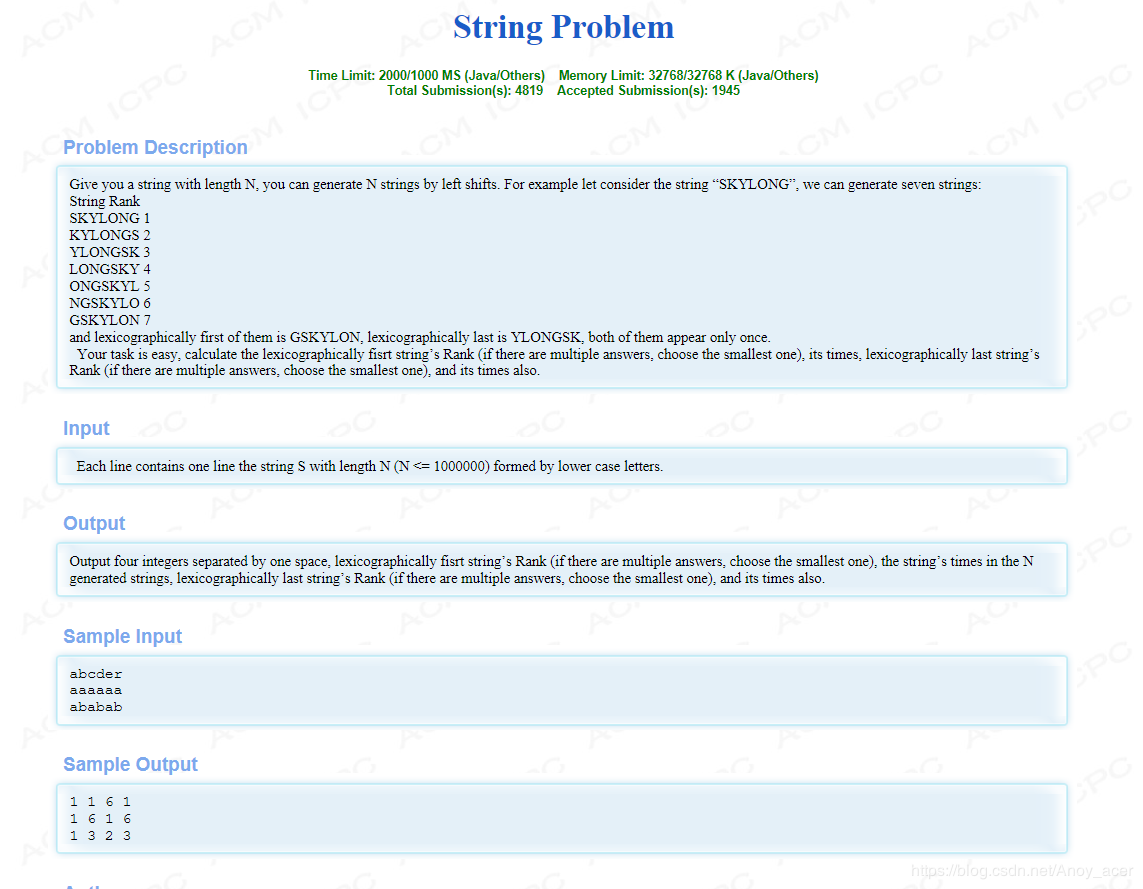
hdu3374 （最小表示法 + 最大表示法）

题意：

给你一个字符串，问这个字符串经过移动后的字典序最小的字符串的首字符位置和字典序最大的字符串的首字符的位置，和能出现多少次最小字典序的字符串和最大字典序的字符串

思路：
利用最小表示法与最大表示法O(n)复杂度求出最小字典序和最大字典序串出现位置，然后利用kmp求出next，利用next数组性质求出循环节次数，因为最小和最大字典序串出现次数等于循环节次数