Python神经网络编程笔记

神经元

想一想便知道，当一个人捏你一下以至于你会痛得叫起来的力度便是神经元的阈值，而我们构建的时候也是把这种现象抽象成一个函数，叫作激活函数。

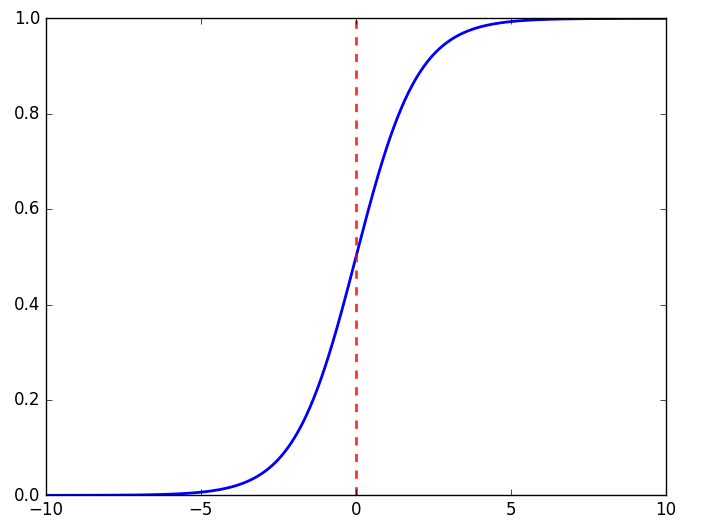
而这里便是我们使用sigmoid函数的原因，它是一个很简单的函数，平滑更接近显示。

$$y=\frac{1}{1+e^{-x}}$$

神经网络传递信号

神经网络便是通过一个一个神经元连接，使用权值x输入的和在通过sigmoid函数得到最终的输出值，然后一层一层的传递下去。

\[O = sigmoid(W\cdot I)
\]

其中，$O$为输出矩阵，$W$为权值矩阵，$I$为输入矩阵。

举个栗子：

假设我们设置一个三层神经网络，分别为输入层，隐藏层（注意：不管我们中间有多少层，中间的都叫隐藏层，我们这里隐藏层只有一层），输出层。

1.输入层->隐藏层：我们输入矩阵是一个(3x1)的矩阵，那么我们设置四个权值，那么我们的第一个权值矩阵（就是输入层->隐藏层的）的维度也就为(4x3)，这时我们相乘也就得到输出矩阵(4x1)，进行下一步时，这个(4x1)的输出矩阵就变成了输入；

2.隐藏层->输出层：这是我们的输入矩阵是一个(4x1)的矩阵，然后我们要求输出层输出为两个值，那么我们第二个权值矩阵（就是隐藏层->输出层的）的维度也就为(2x4)，这时我们相乘也就得到输出矩阵(2x1)，也就为最终的结果了。

反向传播

现在我们已经可以收到由前面的层传输过来的结果了，但答案肯定是不准的，那么我们该如何进行改进呢？

毫无疑问，首先我们要计算误差，假设真实值为t，输出值为o，那么误差e就为:

\[e=t-o
\]

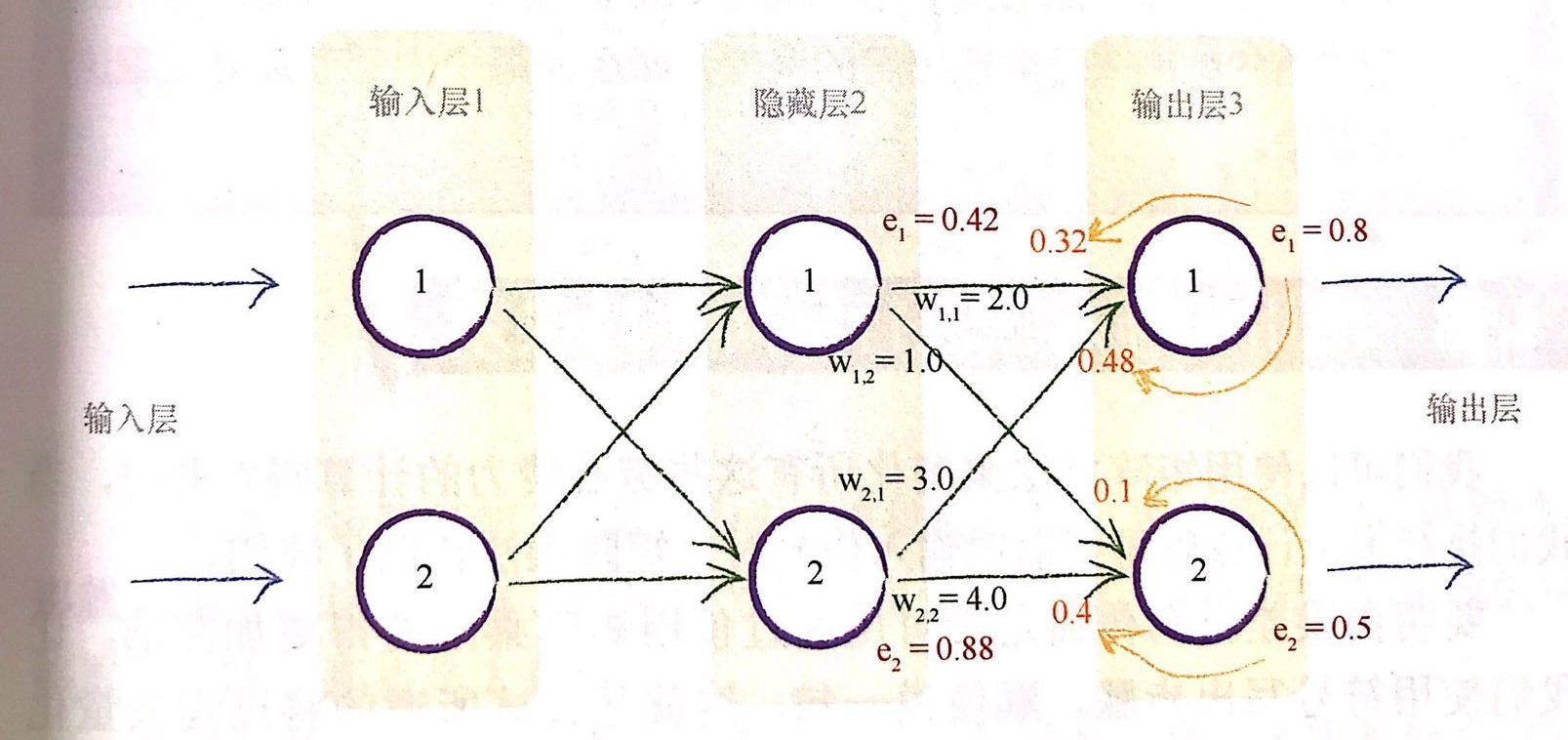
我们按照上图来进行举例说明。

1.更新误差

那么，隐藏层的误差如何确定呢？

我们使用链接$w_{1,1}$和链接$w_{2,1}$上的分割误差之和来进行更新，也就是

\[e_{hidden,1}=e_{output,1}*\frac{w_{1,1}}{w_{1,1}+w_{2,1}}+e_{output,2}*\frac{w_{1,2}}{w_{1,2}+w_{2,2}}
\]

我们也进行带值进行计算

\[0.8*\frac{2}{2+3}+0.5*\frac{1}{1+4}=0.42
\]

2.使用矩阵进行更新

我们发现上面的公式应用到矩阵运算会很复杂，我们究其本质，最重要的事情是输出误差与链接权重$w_{ij}$的乘法。较大的权重就意味着携带较多的输出误差给隐藏层，这些分数的分母是一种归一化因子。如果我们忽略这种因子，那么我们仅仅失去后溃误差的大小。

也就是这里我们使用$e_1*w_{1,1}$来代替$e_1*w_{1,1}/(w_{1,1}+w_{2,1})$ 。那么我们就可以很容易的进行矩阵运算进行误差更新了。

\[error_{hidden}=w^T_{hidden\_output}\cdot error_{output}
\]

3.更新权重

在神经网络中，我们采用梯度下降法来寻找最优的权重值。神经网络本身的输出函数部署一个误差函数，但我们知道，由于误差是目标训练值与实际输出值之间的差值，因此我们可以很容易的构建误差函数，即

\[(目标值-实际值)^2
\]

为什么我们要构建平方项呢？为何不用绝对值误差呢？原因有三

使用误差的平方，我们可以很容易的使用代数计算出梯度下降的斜率；
误差函数平滑连续，这是的梯度下降法很好地发挥作用，没有间断，也没有突然的跳跃；
越接近最小值，梯度越小，这意味着，如果我们使用这个函数调节步长，超调的风险就会变得很小。

现在我们要更新$w_{j,k}$的权值，那么来推导一下它的更新公式：

首先有

\[\frac{\partial E}{\partial W_{j,k}} = \frac{\partial}{\partial W_{j,k}}(t_k-o_k)^2
\]

然后根据链式法则得到：

\[\frac{\partial E}{\partial W_{j,k}} = \frac{\partial E}{\partial o_k} \cdot \frac{\partial o_k}{\partial W_{j,k}}
\]

然后我们对其求偏导：

\[\frac{\partial E}{\partial W_{j,k}} = -2(t_k-o_k) \cdot \frac{\partial o_k}{\partial W_{j,k}}\\
= -2(t_k-o_k) \cdot \frac{\partial}{\partial W_{j,k}}sigmoid(\sum_{j}w_{j,k}\cdot o_j)\\
= -2(t_k-o_k) \cdot sigmoid(\sum_{j}w_{j,k}\cdot o_j)(1-sigmoid(\sum_{j}w_{j,k}\cdot o_j)) \cdot \frac{\partial}{\partial W_{j,k}}(\sum_{j}w_{j,k}\cdot o_j)\\
= -2(t_k-o_k) \cdot sigmoid(\sum_{j}w_{j,k}\cdot o_j)(1-sigmoid(\sum_{j}w_{j,k}\cdot o_j)) \cdot o_j\]

这样我们就得到了最后的权重更新公式：

\[new W_{j,k} = oldW_{j,k} - \alpha \cdot \frac{\partial E}{\partial W_{j,k}}
\]

其中：

\[\frac{\partial E}{\partial W_{j,k}} = \Delta w_{j,k} = \alpha \cdot E_k \cdot O_k(1-O_k) \cdot O_j^T
\]

输入与输出

1.输入

我们观察sigmoid函数注意到，当输入值变大，激活函数也就会越来越平坦，权重的改变取决于激活函数的梯度，小梯度也就意味着限制了神经网络的学习能力，这就是所谓的饱和神经网络。因此，我们要尽量保持小的输入。

但有趣的是，当输入信号太小，计算机便会损失精度，所以我们要保持输入范围在0.0~1.0之间，但输入为0的话会将$o_j$设置为0，这样的权重更新表达式就会等于0，从而造成学习能力的丧失，我们需要加上一个小小的偏移，例如0.01，避免输入0带来的麻烦。

2.输出

我们使用激活函数得到的值的范围会被限制在0~1之间，注意：逻辑函数甚至不能取到1.0，只能接近于1.0.数学家们称之为渐进于1.0.

因此，我们需要调整目标值，匹配激活函数的可能输出，常见的使用范围为0.0_{1.0之间，但我们是取不到0.0和1.0的，所以这里我们也要进行偏移，例如0.01}0.99.

随机初始权重

和输入输出一样，初始的权重设置也要遵从同样地原则。过大的初始权重会造成大的信号传递给激活函数，导致网络饱和，从而降低学习到更好的权重的能力，因此应该避免大的初始权重值。

我们可以从-1.0~+1.0之间随机均匀地挑选初始权重。而我们也希望初始权重的分布是均匀的，经过数学家们的证明，我们有一个比较好的挑选方式，那就是从均值为0、标准方差等于节点传入链接数量平方根倒数的正态分布中进行采样。

总而言之，我们要禁止将初始权重设定为0或者将初始权重设定为像痛得恒定值，这样会很糟糕。

代码实现

import numpy as np

import scipy.special

import matplotlib.pyplot as plt

# neural network class definition

class NeuralNetwork:

    def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):

        # set number of nodes in each input, hidden, output layer

        self.inodes = inputnodes

        self.hnodes = hiddennodes

        self.onodes = outputnodes

        # learning rate

        self.lr = learningrate

        # 初始权重矩阵

        self.wih = np.random.normal(0.0, pow(self.hnodes, -0.5), (self.hnodes, self.inodes))

        self.who = np.random.normal(0.0, pow(self.onodes, -0.5), (self.onodes, self.hnodes))

        # 激活函数

        self.activation_function = lambda x: scipy.special.expit(x)

        pass

    def train(self, inputs_list, targets_list):

        # 输入

        inputs = np.array(inputs_list, ndmin=2).T

        targets = np.array(targets_list, ndmin=2).T

        # 隐藏层计算

        hidden_inputs = np.dot(self.wih, inputs)

        hidden_outputs = self.activation_function(hidden_inputs)

        # 输出层计算

        final_inputs = np.dot(self.who, hidden_outputs)

        final_outputs = self.activation_function(final_inputs)

        # 误差计算

        output_errors = targets - final_outputs

        hidden_errors = np.dot(self.who.T, output_errors)

        # 反向传播更新权值

        self.who += self.lr * np.dot((output_errors * final_outputs * (1.0 - final_outputs)), np.transpose(hidden_outputs))

        self.wih += self.lr * np.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)),  np.transpose(inputs))

        pass

    def query(self, inputs_list):

        # 输入

        inputs = np.array(inputs_list, ndmin=2).T

        # 隐藏层计算

        hidden_inputs = np.dot(self.wih, inputs)

        hidden_outputs = self.activation_function(hidden_inputs)

        # 输出层计算

        final_inputs = np.dot(self.who, hidden_outputs)

        final_outputs = self.activation_function(final_inputs)

        return final_outputs

if __name__ == '__main__':

    input_nodes = 784

    hidden_nodes = 200

    output_nodes = 10

    learning_rate = 0.2

    nn = NeuralNetwork(input_nodes, hidden_nodes, output_nodes, learning_rate)

    # 加载数据

    train_data_file = open("./mnist_train.csv", "r")

    train_data_list = train_data_file.readlines()

    train_data_file.close()

    print("数据读取完毕")

    # 可视化

    # all_values = train_data_list[0].split(',')

    # image_array = np.asfarray(all_values[1:]).reshape((28, 28))

    # plt.imshow(image_array, cmap="Greys", interpolation='None')

    # plt.show()

    epochs = 2

    for e in range(epochs):

        print("\t===== epochs %d =====\t" % (e+1))

        for record in train_data_list:

            all_values = record.split(',')

            inputs = (np.asfarray(all_values[1:]) / 255 * 0.99) + 0.01

            targets = np.zeros(output_nodes) + 0.01

            targets[int(all_values[0])] = 0.99

            nn.train(inputs, targets)

    # 预测

    test_data_file = open("./mnist_test.csv", "r")

    test_data_list = test_data_file.readlines()

    test_data_file.close()

    print(len(test_data_list))

    t_num = 0

    for line in test_data_list:

        all_values = line.split(',')

        y = all_values[0]

        y_pred = np.argmax(nn.query(np.asfarray(all_values[1:]) / 255 * 0.99 + 0.01))

        if int(y) == int(y_pred):

            t_num += 1

    print(t_num)

    print(t_num * 1.0 / len(test_data_list))

这份三层神经网络对mnist手写数据集能达到97%的准确度。