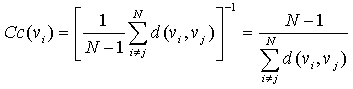PTA数据结构与算法题目集(中文) 7-36 社交网络图中结点的“重要性”计算 (30 分)
PTA数据结构与算法题目集(中文) 7-36 社交网络图中结点的“重要性”计算 (30 分)
在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来。他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用,可以增强也可以减弱。而结点根据其所处的位置不同,其在网络中体现的重要性也不尽相同。
“紧密度中心性”是用来衡量一个结点到达其它结点的“快慢”的指标,即一个有较高中心性的结点比有较低中心性的结点能够更快地(平均意义下)到达网络中的其它结点,因而在该网络的传播过程中有更重要的价值。在有N个结点的网络中,结点vi的“紧密度中心性”(数学上定义为vi到其余所有结点vj (j≠i) 的最短距离(的平均值的倒数:
对于非连通图,所有结点的紧密度中心性都是0。
给定一个无权的无向图以及其中的一组结点,计算这组结点中每个结点的紧密度中心性。
输入格式:
输入第一行给出两个正整数N和M,其中N(≤)是图中结点个数,顺便假设结点从1到N编号;M(≤)是边的条数。随后的M行中,每行给出一条边的信息,即该边连接的两个结点编号,中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K(≤)以及K个结点编号,用空格分隔。
输出格式:
按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性,每个输出占一行,结果保留到小数点后2位。
输入样例:
9 14
1 2
1 3
1 4
2 3
3 4
4 5
4 6
5 6
5 7
5 8
6 7
6 8
7 8
7 9
3 3 4 9
输出样例:
Cc(3)=0.47
Cc(4)=0.62
Cc(9)=0.35
题目分析:这是一道图的 多源最短路问题,利用Floyd算法来解决
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>
#include<malloc.h>
#define INIFITY 65535
typedef struct ENode* Edge;
struct ENode
{
int V1, V2;
};
typedef struct GNode* Graph;
struct GNode
{
int G[][];
float Nv;
int Ne;
}; int IsEdge(Graph Gra, int V1, int V2)
{
return Gra->G[V1][V2]!=INIFITY;
} void Insert(Graph Gra, Edge E)
{
Gra->G[E->V1][E->V2] = ;
Gra->G[E->V2][E->V1] = ;
} Graph CreateGraph(int Nv)
{
Graph Gra = (Graph)malloc(sizeof(struct GNode));
Gra->Nv = Nv;
Gra->Ne = ;
for (int i = ; i <=Gra->Nv; i++)
for (int j = ; j <= Gra->Nv; j++)
{
Gra->G[i][j] = INIFITY;
if (i == j)
Gra->G[i][j] = ;
}
return Gra;
} int Dist[][];
int Flag=;
void Floyd(Graph Gra)
{
int i, j, k;
for (i = ; i <= Gra->Nv; i++)
for (j = ; j <= Gra->Nv; j++)
Dist[i][j] = Gra->G[i][j];
for(int k=;k<=Gra->Nv;k++)
for(int i=;i<=Gra->Nv;i++)
for (int j = ; j <= Gra->Nv; j++)
{
if (Dist[i][k] + Dist[k][j] < Dist[i][j])
Dist[i][j] = Dist[i][k] + Dist[k][j];
}
for (i = ; i <= Gra->Nv; i++)
for (j = ; j <= Gra->Nv; j++)
if (Dist[i][j] == INIFITY)
{
Flag = ;
break;
}
} int main()
{
int N, M;
scanf("%d%d", &N, &M);
Graph Gra = CreateGraph(N);
Gra->Ne = M;
Edge E = (Edge)malloc(sizeof(struct ENode));
for (int i = ; i < Gra->Ne; i++)
{
scanf("%d%d", &(E->V1), &(E->V2));
Insert(Gra, E);
}
Floyd(Gra);
float num=;
int K;
scanf("%d", &K);
while (K--)
{
num = ;
int n;
scanf("%d", &n);
if (Flag)
{
for (int i = ; i <= Gra->Nv; i++)
num += Dist[n][i];
printf("Cc(%d)=%.2f\n", n, (Gra->Nv - ) / num);
}
else
printf("Cc(%d)=0.00\n", n);
}
return ;
}
PTA数据结构与算法题目集(中文) 7-36 社交网络图中结点的“重要性”计算 (30 分)的更多相关文章
- PTA数据结构与算法题目集(中文) 7-32
PTA数据结构与算法题目集(中文) 7-32 7-32 哥尼斯堡的“七桥问题” (25 分) 哥尼斯堡是位于普累格河上的一座城市,它包含两个岛屿及连接它们的七座桥,如下图所示. 可否走过这样的七 ...
- PTA数据结构与算法题目集(中文) 7-15
PTA数据结构与算法题目集(中文) 7-15 7-15 QQ帐户的申请与登陆 (25 分) 实现QQ新帐户申请和老帐户登陆的简化版功能.最大挑战是:据说现在的QQ号码已经有10位数了. 输入格式 ...
- PTA数据结构与算法题目集(中文) 7-43字符串关键字的散列映射 (25 分)
PTA数据结构与算法题目集(中文) 7-43字符串关键字的散列映射 (25 分) 7-43 字符串关键字的散列映射 (25 分) 给定一系列由大写英文字母组成的字符串关键字和素数P,用移位法定义 ...
- PTA数据结构与算法题目集(中文) 7-42整型关键字的散列映射 (25 分)
PTA数据结构与算法题目集(中文) 7-42整型关键字的散列映射 (25 分) 7-42 整型关键字的散列映射 (25 分) 给定一系列整型关键字和素数P,用除留余数法定义的散列函数将关键字映射 ...
- PTA数据结构与算法题目集(中文) 7-41PAT排名汇总 (25 分)
PTA数据结构与算法题目集(中文) 7-41PAT排名汇总 (25 分) 7-41 PAT排名汇总 (25 分) 计算机程序设计能力考试(Programming Ability Test,简称P ...
- PTA数据结构与算法题目集(中文) 7-40奥运排行榜 (25 分)
PTA数据结构与算法题目集(中文) 7-40奥运排行榜 (25 分) 7-40 奥运排行榜 (25 分) 每年奥运会各大媒体都会公布一个排行榜,但是细心的读者发现,不同国家的排行榜略有不同.比如 ...
- PTA数据结构与算法题目集(中文) 7-39魔法优惠券 (25 分)
PTA数据结构与算法题目集(中文) 7-39魔法优惠券 (25 分) 7-39 魔法优惠券 (25 分) 在火星上有个魔法商店,提供魔法优惠券.每个优惠劵上印有一个整数面值K,表示若你在购买某商 ...
- PTA数据结构与算法题目集(中文) 7-38寻找大富翁 (25 分)
PTA数据结构与算法题目集(中文) 7-38寻找大富翁 (25 分) 7-38 寻找大富翁 (25 分) 胡润研究院的调查显示,截至2017年底,中国个人资产超过1亿元的高净值人群达15万人.假 ...
- PTA数据结构与算法题目集(中文) 7-37 模拟EXCEL排序 (25 分)
PTA数据结构与算法题目集(中文) 7-37 模拟EXCEL排序 (25 分) 7-37 模拟EXCEL排序 (25 分) Excel可以对一组纪录按任意指定列排序.现请编写程序实现类似功能. ...
随机推荐
- Hyperledger Fabric1.4环境搭建
参考文档:https://www.cnblogs.com/cbkj-xd/p/11067790.html 1. 设置下载源为阿里源 sudo vim /etc/apt/sources.list 在配置 ...
- 开发RTSP 直播软件 H264 AAC 编码
上一篇对摄像头预览,拍照做了大概的介绍,现在已经可以拿到视频帧了,在加上 RTSP 实现,就是直播的雏形,当然还要加上一些 WEB 管理和手机平台的支援,就是一整套直播软件. 介绍一些基础概念:RTP ...
- ffmpeg 编程常用 pcm 转 aac aac 转 pcm mp4 h264解码
ffmpeg 是现在开源的全能编解码器,基本上全格式都支持,纯 c 语言作成,相对比其它的 VLC ,GStreamer glib2 写的,开发更简单些,文档很棒,就是 examples 比较少. 常 ...
- 使用ajax提交登录
引入jquery-1.10.2.js或者jquery-1.10.2.min.js 页面 <h3>后台系统登录</h3> <form name="MyForm&q ...
- 【春招】 java static 执行顺序
package static类型.执行顺序; public class Test { Person person = new Person("Test"); static{ Sys ...
- 【剑指Offer】简单部分每日五题 - Day 1
今天开始更新leetcode上<剑指Offer>的题解,先从简单难度开始.预计按下列顺序更新: 简单难度:每日5题 中等难度:每日3题 困难难度:每日1题 17 - 打印从1到最大的n位数 ...
- 【Android】四大组件归纳总结
随着学习持续更新 四大组件均可使用android:process="name"在Manifest中声明成独立进程 Activity 生命周期 4种启动模式 Android使用回退栈 ...
- Python操作系统
一 为什么要有操作系统 (两本书:现代操作系统.操作系统原理,学好python以后再去研究吧~~) 现代的计算机系统主要是由一个或者多个处理器,主存,硬盘,键盘,鼠标,显示器,打印机,网络接口及其他输 ...
- javaScript 基础知识汇总(八)
1.Map Set WeakMap 和WeakSet Map 是一个键值对的集合,主要的方法包括: new Map() 创建Map map.set(key,value) 根据键(key)存储值(va ...
- @on-row-click="$emit('on-row-click', arguments[0], arguments[1])" 行内返回事件的一种写法
@on-row-click="$emit('on-row-click', arguments[0], arguments[1])"