POJ 2057 The Lost Home 树形dp 难度:2

The Lost House

Time Limit: 3000MS		Memory Limit: 30000K
Total Submissions: 2203		Accepted: 906

Description

One day a snail climbed up to a big tree and finally came to the end of a branch. What a different feeling to look down from such a high place he had never been to before! However, he was very tired due to the long time of climbing, and fell asleep. An unbelievable thing happened when he woke up ---- he found himself lying in a meadow and his house originally on his back disappeared! Immediately he realized that he fell off the branch when he was sleeping! He was sure that his house must still be on the branch he had been sleeping on. The snail began to climb the tree again, since he could not live without his house.

When reaching the first fork of the tree, he sadly found that he could not remember the route that he climbed before. In order to find his lovely house, the snail decided to go to the end of every branch. It was dangerous to walk without the protection of the house, so he wished to search the tree in the best way.

Fortunately, there lived many warm-hearted worms in the tree that could accurately tell the snail whether he had ever passed their places or not before he fell off.

Now our job is to help the snail. We pay most of our attention to two parts of the tree ---- the forks of the branches and the ends of the branches, which we call them key points because key events always happen there, such as choosing a path, getting the help from a worm and arriving at the house he is searching for.

Assume all worms live at key points, and all the branches between two neighboring key points have the same distance of 1. The snail is now at the first fork of the tree.

Our purpose is to find a proper route along which he can find his house as soon as possible, through the analysis of the structure of the tree and the locations of the worms. The only restriction on the route is that he must not go down from a fork until he has reached all the ends grown from this fork.

The house may be left at the end of any branches in an equal probability. We focus on the mathematical expectation of the distance the snail has to cover before arriving his house. We wish the value to be as small as possible.

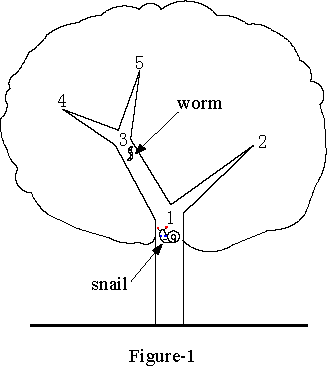
As illustrated in Figure-1, the snail is at the key point 1 and his house is at a certain point among 2, 4 and 5. A worm lives at point 3, who can tell the snail whether his house is at one of point 4 and 5 or not. Therefore, the snail can choose two strategies. He can go to point 2 first. If he cannot find the house there, he should go back to point 1, and then reaches point 4 (or 5) by point 3. If still not, he has to return point 3, then go to point 5 (or 4), where he will undoubtedly find his house. In this choice, the snail covers distances of 1, 4, 6 corresponding to the circumstances under which the house is located at point 2, 4 (or 5), 5 (or 4) respectively. So the expectation value is (1 + 4 + 6) / 3 = 11 / 3. Obviously, this strategy does not make full use of the information from the worm. If the snail goes to point 3 and gets useful information from the worm first, and then chooses to go back to point 1 then towards point 2, or go to point 4 or 5 to take his chance, the distances he covers will be 2, 3, 4 corresponding to the different locations of the house. In such a strategy, the mathematical expectation will be (2 + 3 + 4) / 3 = 3, and it is the very route along which the snail should search the tree.

Input

The input contains several sets of test data. Each set begins with a line containing one integer N, no more than 1000, which indicates the number of key points in the tree. Then follow N lines describing the N key points. For convenience, we number all the key points from 1 to N. The key point numbered with 1 is always the first fork of the tree. Other numbers may be any key points in the tree except the first fork. The i-th line in these N lines describes the key point with number i. Each line consists of one integer and one uppercase character 'Y' or 'N' separated by a single space, which represents the number of the previous key point and whether there lives a worm ('Y' means lives and 'N' means not). The previous key point means the neighboring key point in the shortest path between this key point and the key point numbered 1. In the above illustration, the previous key point of point 2 or 3 is point 1, while the previous key point of point 4 or 5 is point 3. This integer is -1 for the key point 1, means it has no previous key point. You can assume a fork has at most eight branches. The first set in the sample input describes the above illustration.

A test case of N = 0 indicates the end of input, and should not be processed.

Output

Output one line for each set of input data. The line contains one float number with exactly four digits after the decimal point, which is the mathematical expectation value.

Sample Input

5
-1 N
1 N
1 Y
3 N
3 N
10
-1 N
1 Y
1 N
2 N
2 N
2 N
3 N
3 Y
8 N
8 N
6
-1 N
1 N
1 Y
1 N
3 N
3 N
0

Sample Output

3.0000
5.0000
3.5000
题意:有一只蜗牛丢了壳现在要爬树找回来,这棵树上有些地方有善良的虫子告诉它,它的壳是不是在这枝桠上,现在不知道壳在哪个叶节点上,问怎么选择走的顺序,平均长度期望最小,输出平均长度期望
思路:
0.1 看到这个期望,必须发现的是过程只要不除以叶节点数就可以过程中不出现浮点数,只计算某种最优路径选择,使得分别到达各点的所需长度之和最短即可,
0.2 首先看去掉虫子的影响来看这棵树,我们知道树的问题的一大特点就是把整棵树换成各子树和根节点之间的某种运算
1 怎么样把走多次树变成走一次树呢?(如果要是走n次铁定就超时了),仔细看看树,如果选择先走某枝桠,这棵树上的叶节点有两种可能,A:在这个枝桠上,B:不在这个枝桠上,
B:当我们选择了先走这棵枝桠的时候就必须走一遍这棵枝桠的每一个节点,(假设没虫)于是我们设这个长度为bak(back)[i],对于子节点j,bak[i]=sigma(bak[j]+2)
A:不断重复选择先走那一只子节点,一直走到叶节点为止,所花费的时间是之前走过的无用枝桠长度(+从根节点到达那些子节点的长度)+到达这个叶节点不返回的长度,可是这个只对于叶节点有意义,对于非叶节点,我们设scan[i]为遍历到所有它的子叶节点,从i点出发的所有路径长度之总和(的最小值),设i的子节点为j,k,j是现在要走的节点,k是已经走过的节点,scan[i]=sigma(lef[j]*(1(出发到子节点的步数+sigma(bak[k]+2)(前面多走的路+往返这些子节点))+scan[j](遍历这些j上的子节点))
对于叶节点,明显bak[i]=scan[i]=0

2 现在算是有确定了遍历顺序时的计算公式了,可是怎么确定遍历子节点的顺序呢?对于外部,只有scan[i]重要,所以子节点的顺序要使scan[i]最小,排列的话肯定超时,只能用贪心了
任取两个节点j1,j2,假设j1在j2前面的scan[i]=S1,j2在j1前面的scan[i]=S2,S1-S2=(lef[j1]*(bak[j2]+2)-lef[j2]*(bak[j1]+2)),整理一下,要让这个值小于零,应该有lef[j1]/(bak[j1]+2)小于lef[j2]/(bak[j2]+2),这时候j1更优,显然按这个值增序排序就可以确定选取顺序了

3 现在加上虫子的影响,如果有虫的话虫子会告诉蜗牛不用经过这个点,也即bak[i]=0

错误次数:5 
原因: 1 bak[s]+=bak[son]+2;忘了+2,测试数据太弱没测出来 2 double ans=(double)scan[1]/(double )lef[1];直接除以lef了 3 lef没有memset 4 弃疗随便交

#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int maxn=1002;
long long scan[maxn],bak[maxn];
int lef[maxn];
bool worm[maxn];
int len[maxn];
int e[maxn][maxn];
int n;
char buff[2];
typedef pair<double,int> P;
void dfs(int s){
    if(len[s]==0){
        scan[s]=bak[s]=0;
        lef[s]=1;
        return ;
    }
    priority_queue<P,vector<P>,greater<P> >que;
    for(int i=0;i<len[s];i++){
        dfs(e[s][i]);
        lef[s]+=lef[e[s][i]];
    }
     for(int i=0;i<len[s];i++){
        que.push(P((double)(bak[e[s][i]]+2)/(double )lef[e[s][i]],e[s][i]));
    }
    int son,sum=0;
    for(int i=1;!que.empty();i++){
        long long tmp=que.top().first;
        son=que.top().second;que.pop();
        sum+=lef[son];
        scan[s]+=scan[son]+lef[son]+(2+bak[son])*(lef[s]-sum);
        bak[s]+=bak[son]+2;
    }
   if(worm[s]) bak[s]=0;
}

int main(){
    while(scanf("%d",&n)==1&&n){
        memset(len,0,sizeof(len));
        memset(worm,0,sizeof(worm));
        memset(scan,0,sizeof(scan));
        memset(bak,0,sizeof(bak));
        memset(lef,0,sizeof(lef));
        for(int i=1;i<=n;i++){
            int f;
            scanf("%d%s",&f,buff);
            if(f>0){
                e[f][len[f]++]=i;
            }
            if(buff[0]=='Y')worm[i]=true;
        }
        dfs(1);
        double ans=(double)scan[1]/(double )lef[1];
        printf("%.4f\n",ans);
    }
    return 0;
}