HDU2044 小蜜蜂斐波那契

一只小蜜蜂...

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 58392    Accepted Submission(s):
21093

Problem Description

有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房，不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。
其中，蜂房的结构如下所示。

 

Input

输入数据的第一行是一个整数N,表示测试实例的个数，然后是N
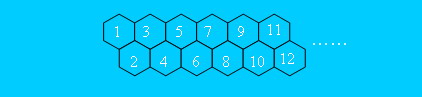
行数据，每行包含两个整数a和b(0<a<b<50)。

 

Output

对于每个测试实例，请输出蜜蜂从蜂房a爬到蜂房b的可能路线数，每个实例的输出占一行。

 

Sample Input

2
1 2
3 6

 

Sample Output

1
3

 

Author

lcy

 

Source

递推求解专题练习（For
Beginner）

 

Recommend

lcy   |   We have carefully selected several similar
problems for you:  2045 2046 2050 2041 2047 

注意用long long 而不是int 。int 会溢出

#include <iostream>
#include <stdlib.h>
#include <stdio.h>
using namespace std;
];
int main()
{
    int i,n,m,t;
    a[]=;
    a[]=;
    ;i<=;i++)
    a[i]=a[i-]+a[i-];
    cin>>t;
    while(t--)
    {
        cin>>n>>m;
        cout<<a[m-n]<<endl;
    }
    ;
}