[jzoj]3521.道路覆盖(cover)

Link

　　https://jzoj.net/senior/#main/show/3521

Description

　　Tar把一段凹凸不平的路分成了高度不同的N段，并用H[i]表示第i段高度。现在Tar一共有n种泥土可用，它们都能覆盖给定的连续的k个部分。对于第i种泥土，它的价格为C[i]，可以使得区间[i,min(n,i+k-1)] 的路段的高度增加E[i]。Tar要设定一种泥土使用计划，使得使用若干泥土后，这条路最低的高度尽量高，并且这个计划必须满足以下两点要求：
　　（1）每种泥土只能使用一次。
　　（2）泥土使用成本必须小于等于M。
　　请求出这个最低的高度最高是多少。

Solution

30分

　　事实上，数据是允许拿到90分的，我们直接跑一次递归就可以了，记录最低值的最高值

100分

　　这个的状压DP很巧妙，从来没做过这种不需要存所有状态的状压DP

　　从“最低的高度最高”就可以看出，这道题是用二分的，正解就是二分答案。

　　从而，我们就把这道题目变为一道判定性的问题，给出一个mid，问你是否符合上面的题意。

　　普通方法使用递归判断可行性

　　既然可以用递归，那么显然可以用动态规划。

　　我们设F[i,s]表示你当前想选第i种泥土，前面k种的状态（包括i）是什么，用二进制表示,，0表示在那个位置没用了泥土，1表示用了。（用没用表示从他开始往后铺，专属于他的泥土）一定要看下面第二个图

　　我们用当前F[i,s]去更新F[i+1,s1]

　　关键是我们怎么转移。

　　对于每一种泥土，只有选和不选两种状态，那么我们只要考虑这两种情况就可以了

　　在此之前，我们先看一个东西

　　

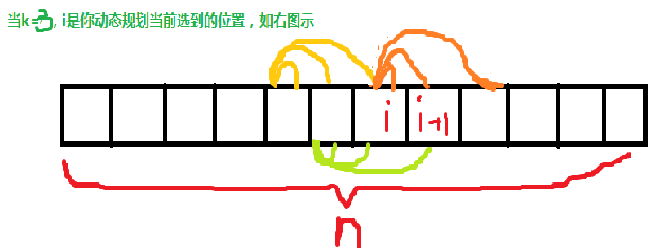
　　注意，我们这里是用i，更新i+1

　　读图可以发现，对i+1有影响的只有从i前k-1个（包括i）

　　可以发现，只有i包括i的前k-1个对i+1是有影响的。

　　因为你选到i时，状态是s，那么，如果从i更新到i+1，状态就是s去掉最后一位，也就是(s>>1)，其实就是s/2

　　我们统计s状态中，有哪个地方是选了泥土的，然后记录一下，他们一共会让i+1这个位置的土地高多少，设这个数为num，要多看图，多写草稿

　　为什么呢，因为前面的加了对应的e数组的某一个值，又因为它会影响到当前这个位置，看上图，所以，我们要看看，他们究竟影响到i+1这个位置增加多少值，所以我们要提前记录下来

　　其中S是枚举的！枚举的！枚举的！

　　

　　①不选

　　如果不选，那么num+h[i]必定是大于等于mid的，这样才符合题目要求，如果不懂反复读上面的那句话，看看我画出来精美的图，就知道了。不懂都会懂

　　满足的上面的情况，我们就可以转移了

　　f[i+1,s>>1]:=min(f[i+1,s>>1]，f[i,s])　

　　②选

　　如果选，就要满足num+h[i]+E[i]是大于等于mid的，同理也是上面所说

　　那么当前的位置s状态中i+1的位置应该是1，所以，我们就是要更新新的s

　　f[i+1,s>>1 or 1 shl (k-1)]:=min(f[i+1,s>>1 or 1 shl (k-1)]，f[i,j]+c[i]);

　　最后答案的判断就是判断有没有一个被更改过值得f[n,i](i是状态)是小于等于m的，因为在前面的操作中，都保证了更新过的f数组是符合题目要求的

　　这道题充分的体现了动态规划的屌

Code

uses math;
var
        n,m,k,i,j,l,r,mid:longint;
        a,b,c:array[..] of longint;
        f:array[..,..] of longint;
function pd(x:longint):boolean;
var
        i,j,jj,num:longint;
begin
        fillchar(f,sizeof(f),);

        f[,]:=;

        for i:= to n- do
        begin
                for j:= to  shl k- do
                        if f[i,j]<>- then
                        begin
                                num:=;
                                for jj:=k- downto  do
                                        if ( shl(jj)) and j<> then
                                                inc(num,b[i-(k-jj-)]);

                                if num+a[i+]>=x then
                                    if f[i+,j shr ]<>- then
                                        f[i+,j shr ]:=min(f[i+,j shr ],f[i,j])
                                    else
                                        f[i+,j shr ]:=f[i,j];

                                if num+a[i+]+b[i+]>=x then
                                    if f[i+,j shr + shl (k-)]<>- then
                                        f[i+,j shr + shl (k-)]:=min(f[i+,j shr + shl (k-)],f[i,j]+c[i+])
                                    else
                                        f[i+,j shr + shl (k-)]:=f[i,j]+c[i+];
                        end;
        end;

        for i:= to  shl k- do
                if f[n,i]<>- then
                        if f[n,i]<=m then
                                exit(true);

        exit(false);

end;
begin
        assign(input,'cover.in');reset(input);
        assign(output,'cover.out');rewrite(output);
        readln(n,m,k);
        for i:= to n do
                readln(a[i],b[i],c[i]);

        l:=;
        r:=maxlongint-;
        while l<=r do
        begin
                mid:=(l+r) shr ;

                if pd(mid) then
                        l:=mid+
                else
                        r:=mid-;
        end;

        writeln(l-);
end.