[Luogu P1886]滑动窗口--单调队列入门

题目描述

现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

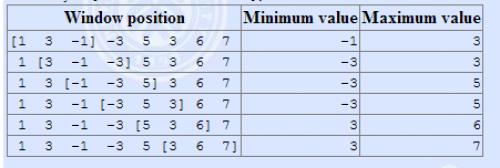
输入输出格式

输入格式：

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX).

输出格式：

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

这题是单调队列入门题。题意清晰明了，求区间最大（小）。第一反应是线段树或者RMQ，但是数据范围爆炸。这道题和普通的区间的区别就在于它的区间长度是固定的。所以使用时间复杂度为O(n)的单调队列来解决。

什么是单调队列呢？单调队列是一种特殊的双端队列，其内部具有单调性（有点像优先序列，但有着本质区别）。

如何实现插入？从队尾插入，若破坏了单调性，则删除队尾元素（这个删除决定了什么题能用什么题不能用），直到找到一个不影响的位置。

如何实现输出？访问队首（真是方便）

如何解决这道题？首先设一个区间为（l,r），则有max(l+1,r+1)=max(a[r+1],max(a[l+1],a[l+2]...a[r])),那么max（l+1,r+1）与max（l,r）其实是有很大一部分重叠的，那么在问题实现的时候就只需要先删除单调队列中不在区间里的数（a[l]），再插入新数(a[r+1])，剩余的不变，就可以解决了。

代码：

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 using namespace std;
 inline int read(){
     int res=,f=;
     char ch=getchar();
     while(ch<''||ch>''){
         if(ch=='-')f=-;
         ch=getchar();
     }
     while(ch>=''&&ch<=''){
         res=res*+(ch-'');
         ch=getchar();
     }
     return res*f;
 }
 const int N=1e6+;
 int nsf[N],nbf[N],que[N],number[N],a[N];
 int n,k,head,tail;
 inline void INT(){
     n=read();k=read();
     for(int i=;i<=n;++i)a[i]=read();
 }
 inline void findmin(){
     head=;tail=;//队头、尾初始化
     for(int i=;i<=n;++i){//插入a[i]到单调序列
         while(number[head]<i-k+&&head<=tail)++head;
         //从队首开始找，“过时”的删除
         while(a[i]<=que[tail]&&head<=tail)--tail;
         //插入时从队尾插入，维护单调上升性质
         number[++tail]=i;que[tail]=a[i];
         //number保存插入时的“时间戳”，que表示值
         nsf[i]=que[head];//当前队列中最小值
     }
 }
 inline void findmax(){
     head=;tail=;
     for(int i=;i<=n;++i){
         while(number[head]<i-k+&&head<=tail)++head;
         while(a[i]>=que[tail]&&head<=tail)--tail;
         number[++tail]=i;que[tail]=a[i];
         nbf[i]=que[head];
     }
 }
 int main(){
 INT();//输入
 findmin();//动态规划求单调队列最小值
 findmax();
 for(int i=k;i<=n;++i)printf("%d ",nsf[i]);
 cout<<endl;
 for(int i=k;i<=n;++i)printf("%d ",nbf[i]);
 return ;
 }

第一次写随笔还有点小兴奋呢~