算法系列：Shell 排序

Copyright © 1900-2016, NORYES, All Rights Reserved.

http://www.cnblogs.com/noryes/

欢迎转载，请保留此版权声明。

-----------------------------------------------------------------------------------------

希尔排序是1959 年由D.L.Shell 提出来的，相对直接排序有较大的改进。希尔排序又叫缩小增量排序

基本思想：

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行依次直接插入排序。

操作方法：

1. 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
2. 按增量序列个数k，对序列进行k 趟排序；
3. 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

希尔排序的示例：

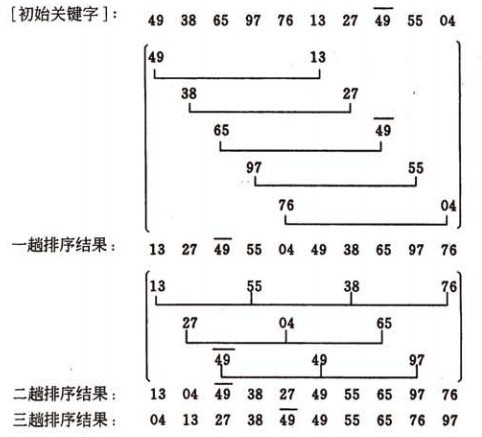
算法实现：

我们简单处理增量序列：增量序列d = {n/2 ,n/4, n/8 .....1} n为要排序数的个数

即：先将要排序的一组记录按某个增量d（n/2,n为要排序数的个数）分成若干组子序列，每组中记录的下标相差d.对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序。继续不断缩小增量直至为1，最后使用直接插入排序完成排序。

1. void print(int a[], int n ,int i){
2. cout<<i <<":";
3. for(int j= 0; j<8; j++){
4. cout<<a[j] <<" ";
5. }
6. cout<<endl;
7. }
8. /**
9. * 直接插入排序的一般形式
10. *
11. * @param int dk 缩小增量，如果是直接插入排序，dk=1
12. *
13. */
14. void ShellInsertSort(int a[], int n, int dk)
15. {
16. for(int i= dk; i<n; ++i){
17. if(a[i] < a[i-dk]){          //若第i个元素大于i-1元素，直接插入。小于的话，移动有序表后插入
18. int j = i-dk;
19. int x = a[i];           //复制为哨兵，即存储待排序元素
20. a[i] = a[i-dk];         //首先后移一个元素
21. while(x < a[j]){     //查找在有序表的插入位置
22. a[j+dk] = a[j];
23. j -= dk;             //元素后移
24. }
25. a[j+dk] = x;            //插入到正确位置
26. }
27. print(a, n,i );
28. }
29. }
30. /**
31. * 先按增量d（n/2,n为要排序数的个数进行希尔排序
32. *
33. */
34. void shellSort(int a[], int n){
35. int dk = n/2;
36. while( dk >= 1  ){
37. ShellInsertSort(a, n, dk);
38. dk = dk/2;
39. }
40. }
41. int main(){
42. int a[8] = {3,1,5,7,2,4,9,6};
43. //ShellInsertSort(a,8,1); //直接插入排序
44. shellSort(a,8);           //希尔插入排序
45. print(a,8,8);
46. }

希尔排序时效分析很难，关键码的比较次数与记录移动次数依赖于增量因子序列d的选取，特定情况下可以准确估算出关键码的比较次数和记录的移动次数。目前还没有人给出选取最好的增量因子序列的方法。增量因子序列可以有各种取法，有取奇数的，也有取质数的，但需要注意：增量因子中除1 外没有公因子，且最后一个增量因子必须为1。希尔排序方法是一个不稳定的排序方法。

 /**
 * Shellsort, using Shell's (poor) increments.
 */
 template <class T>
 void DLLALGOLIB shellSort(std::vector<T>& coll)
 {
     for (int gap = (int).size() / ; gap > ; gap /= )
     {
         for (int idx = gap; idx < (int)coll.size(); ++idx)
         {
             t tmp = coll[i];
             int j = idx;

             for (; j >= gap && tmp < coll[j - gap]; j -= gap)
             {
                 coll[j] = coll[j - gap];
             }

             coll[j] = tmp;
         }
     }
 }