《C# GDI+ 破境之道》：第一境 GDI+基础 —— 第三节：画圆形

有了上一节画矩形的基础，画圆形就不要太轻松+EZ：）所以，本节在画边线及填充上，就不做过多的讲解了，关注一下画“随机椭圆”、“正圆”、“路径填充”的具体实现就好。与画矩形相比较，画椭圆与之完全一致，没有任何特别之处。

在画矩形时，我们使用：

• System.Drawing.Graphics.DrawRectangle(Brush brush, Rectangle rect);
• System.Drawing.Graphics.FillRectangle(Brush brush, Rectangle rect);

在画圆形时，我们使用：

• System.Drawing.Graphics.DrawEllipse(Brush brush, Rectangle rect);
• System.Drawing.Graphics.FillEllipse(Brush brush, Rectangle rect);

看到了吧，就换了个方法名，参数连名都没换：）

所以，了解了如何画矩形，画圆形就是自然掌握的了。

本节就不多费口舌重复了：

 namespace MikeWare.GdiPlus.Ellipses
 {
     using System;
     using System.Collections.Generic;
     using System.Drawing;
     using System.Drawing.Drawing2D;
     using System.Windows.Forms;

     public partial class FormDrawEllipses : Form
     {
         private Random random = null;
         private Color penColor = Color.Transparent;

         public FormDrawEllipses()
         {
             InitializeComponent();
             random = new Random(DateTime.Now.Millisecond);
             penColor = GetRandomColor();
         }

         private Point GetRandomPoint()
         {
             return new Point(random.Next(, ClientRectangle.Width), random.Next(, ClientRectangle.Height - pnlToolbox.Height));
         }

         private Rectangle GetRandomRectangle()
         {
             var pointA = GetRandomPoint();
             var pointB = GetRandomPoint();

             return new Rectangle(Math.Min(pointA.X, pointB.X)
                 , Math.Min(pointA.Y, pointB.Y)
                 , Math.Abs(pointA.X - pointB.X)
                 , Math.Abs(pointA.Y - pointB.Y));
         }

         private Color GetRandomColor()
         {
             return Color.FromArgb(random.Next(, ), random.Next(, ), random.Next(, ));
         }

         private void ShowInformation(string message)
         {
             lblInformation.Text = message;
         }

         private void btnChangePenColor_Click(object sender, EventArgs e)
         {
             if (colors.ShowDialog(this) == DialogResult.OK)
             {
                 penColor = colors.Color;
             }
         }

         private void btnSwitchDoubleBuffered_Click(object sender, EventArgs e)
         {
             DoubleBuffered = !DoubleBuffered;

             ShowInformation($"二级缓冲：{DoubleBuffered}。");
         }

         private void btnDrawRandomEllipse_Click(object sender, EventArgs e)
         {
             var rectangle = GetRandomRectangle();

             var style = (DashStyle)(random.Next(, ));
             var dashCaps = new List<int> { , ,  };
             var dashCap = (DashCap)dashCaps[random.Next(, )];

             using (var g = CreateGraphics())
             using (var pen = new Pen(penColor, 4f))
             using (var brush = new LinearGradientBrush(rectangle, Color.Red, Color.Blue, LinearGradientMode.ForwardDiagonal))
             {
                 g.Clear(SystemColors.AppWorkspace);
                 g.SmoothingMode = SmoothingMode.HighQuality;
                 pen.DashStyle = style;
                 pen.DashCap = dashCap;
                 g.DrawEllipse(pen, rectangle);
             }

             ShowInformation($"随机椭圆，{rectangle}，虚线冒：{dashCap.ToString()}，线条样式：{style.ToString()}。");
         }

         private void btnDrawRandomCircle_Click(object sender, EventArgs e)
         {
             var rectangle = GetRandomRectangle();
             var diameter = Math.Min(rectangle.Size.Width, rectangle.Size.Height);
             rectangle = new Rectangle(rectangle.Location, new Size(diameter, diameter));

             var style = (DashStyle)(random.Next(, ));
             var dashCaps = new List<int> { , ,  };
             var dashCap = (DashCap)dashCaps[random.Next(, )];

             using (var g = CreateGraphics())
             using (var pen = new Pen(penColor, 4f))
             using (var brush = new LinearGradientBrush(rectangle, Color.Red, Color.Blue, LinearGradientMode.ForwardDiagonal))
             {
                 g.Clear(SystemColors.AppWorkspace);
                 g.SmoothingMode = SmoothingMode.HighQuality;
                 pen.DashStyle = style;
                 pen.DashCap = dashCap;
                 g.DrawEllipse(pen, rectangle);
             }

             ShowInformation($"正圆，{rectangle}，虚线冒：{dashCap.ToString()}，线条样式：{style.ToString()}。");
         }

         private void btnFillWithPathGradientBrush_Click(object sender, EventArgs e)
         {
             var rectangle = GetRandomRectangle();

             var wrapMode = (WrapMode)(random.Next(, ));

             //var points = new Point[] { GetRandomPoint(), GetRandomPoint(), GetRandomPoint(), GetRandomPoint(), GetRandomPoint() };
             var points = new Point[] { GetRandomPoint(), GetRandomPoint(), GetRandomPoint() };

             using (var g = CreateGraphics())
             using (var brush = new PathGradientBrush(points, wrapMode))
             {
                 g.Clear(SystemColors.AppWorkspace);
                 g.SmoothingMode = SmoothingMode.HighQuality;
                 g.DrawEllipse(Pens.LightGray, rectangle);
                 g.FillEllipse(brush, rectangle);
             }

             ShowInformation($"路径填充，{rectangle}，WrapMode：{wrapMode}。");
         }
     }
 }

画圆 —— FormDrawEllipses

同样，一个窗体项目，窗体的布局风格与上一节的保持一致：

几个方法不细说，直接上几个效果图草草了事……

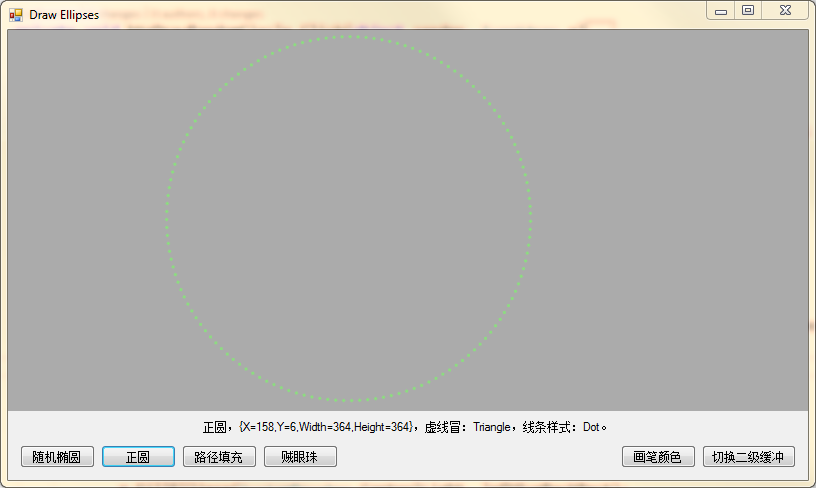
正圆就是一种特殊的椭圆，它的rectangle的宽与高相等；

随机路径填充也蛮有意思的，有的图画，我都想直接那类做logo了：）

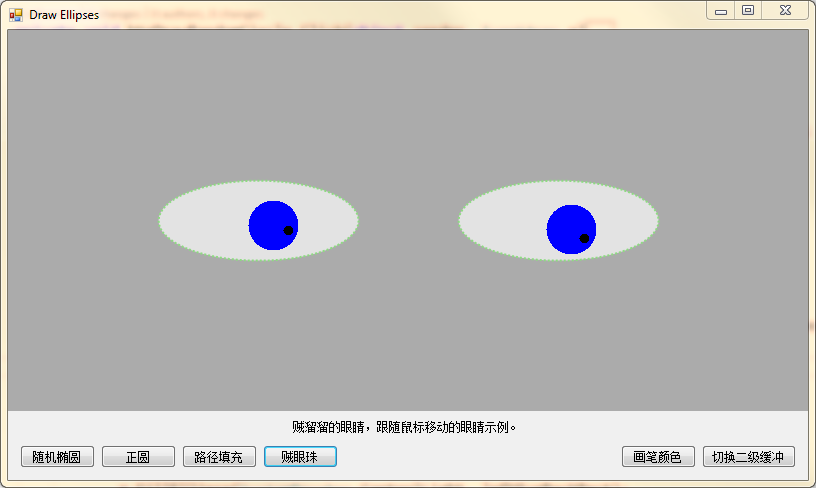
好了，画圆的部分，内容就这么多，按照惯例，那么我们就来利用现有的知识，再耍个花活，画个贼溜溜的眼珠：）

private int maxDistance = ;    // 最大移动距离，用来衡量鼠标距离眼球中心位置的极限；以这个距离极限，来等比缩放眼球移动的距离；
private Rectangle leftEyeBorderRect = Rectangle.Empty   // 左眼眼眶
    , rightEyeBorderRect = Rectangle.Empty              // 右眼眼眶
    , leftEyeBackRect = Rectangle.Empty                 // 左眼兰眼球
    , rightEyeBackRect = Rectangle.Empty                // 右眼兰眼球
    , leftEyeFrontRect = Rectangle.Empty                // 左眼黑眼珠
    , rightEyeFrontRect = Rectangle.Empty;              // 右眼黑眼珠

定义几个私有变量

注释里说明了这几个变量的意义；

 private void btnDrawFollowMouseEyes_Click(object sender, EventArgs e)
 {
     var center = new Point(ClientRectangle.Width / , (ClientRectangle.Height - pnlToolbox.Height) / );
     leftEyeBorderRect = new Rectangle(center.X - , center.Y - , , );
     rightEyeBorderRect = new Rectangle(center.X + , center.Y - , , );
     maxDistance = ClientRectangle.Width < (ClientRectangle.Height - pnlToolbox.Height)
         ? center.X -  - ClientRectangle.X
         : center.Y - ClientRectangle.Y;

     var style = (DashStyle)(random.Next(, ));
     var dashCaps = new List<int> { , ,  };
     var dashCap = (DashCap)dashCaps[random.Next(, )];

     using (var g = CreateGraphics())
     using (var pen = new Pen(penColor, 2f))
     using (var brush = new SolidBrush(penColor))
     {
         g.Clear(SystemColors.AppWorkspace);
         g.SmoothingMode = SmoothingMode.HighQuality;
         pen.DashStyle = style;
         pen.DashCap = dashCap;
         g.FillEllipse(SystemBrushes.ControlLight, leftEyeBorderRect);
         g.DrawEllipse(pen, leftEyeBorderRect);
         g.FillEllipse(SystemBrushes.ControlLight, rightEyeBorderRect);
         g.DrawEllipse(pen, rightEyeBorderRect);
     }

     FormDrawEllipses_MouseMove(null, new MouseEventArgs(MouseButtons.Left, , , , ));

     ShowInformation($"贼溜溜的眼睛，跟随鼠标移动的眼睛示例。");
 }

贼眼珠按钮事件 —— btnDrawFollowMouseEyes_Click

这个事件中，主要就是画出眼眶和填充眼白；

 private void FormDrawEllipses_MouseMove(object sender, MouseEventArgs e)
 {
     if (Rectangle.Empty.Equals(leftEyeBorderRect) || Rectangle.Empty.Equals(rightEyeBorderRect))
         return;

     using (var g = CreateGraphics())
     using (var pen = new Pen(penColor, 2f))
     using (var brush = new SolidBrush(penColor))
     {
         if (Rectangle.Empty != leftEyeBackRect)
             g.FillEllipse(SystemBrushes.ControlLight, leftEyeBackRect);
         if (Rectangle.Empty != rightEyeBackRect)
             g.FillEllipse(SystemBrushes.ControlLight, rightEyeBackRect);
         leftEyeBackRect = CalcRect(leftEyeBorderRect, e.Location, maxDistance, , );
         rightEyeBackRect = CalcRect(rightEyeBorderRect, e.Location, maxDistance, , );
         leftEyeFrontRect = CalcRect(leftEyeBackRect, e.Location, maxDistance, , );
         rightEyeFrontRect = CalcRect(rightEyeBackRect, e.Location, maxDistance, , );

         brush.Color = Color.Blue;
         g.FillEllipse(brush, leftEyeBackRect);
         g.FillEllipse(brush, rightEyeBackRect);

         brush.Color = Color.Black;
         g.FillEllipse(brush, leftEyeFrontRect);
         g.FillEllipse(brush, rightEyeFrontRect);

         g.Flush();
     }
 }

窗体的鼠标移动事件 —— FormDrawEllipses_MouseMove

这个事件里，首先就是将上一次兰眼球的范围填充成眼白的颜色，然后就是根据当前鼠标位置，重新计算兰眼球和黑眼珠的位置，然后进行填充。

这样就形成了一个动态效果了。

 private Rectangle CalcRect(Rectangle baseRect, Point mouseLocation, int maxDistance, int maxMoveDistance, int radius)
 {
     var baseCenter = Point.Add(baseRect.Location, new Size(baseRect.Width / , baseRect.Height / ));

     var radian = Math.Atan2((mouseLocation.Y - baseCenter.Y), (mouseLocation.X - baseCenter.X));

     var mouseDistance = Math.Min(maxDistance, Math.Sqrt(Math.Pow(mouseLocation.X - baseCenter.X, ) + Math.Pow(mouseLocation.Y - baseCenter.Y, )));

     var moveDistance = maxMoveDistance * (mouseDistance / maxDistance);

     var targetCenter = new Point((int)Math.Ceiling(moveDistance * Math.Cos(radian) + baseCenter.X), (int)Math.Ceiling(moveDistance * Math.Sin(radian)) + baseCenter.Y);

     return new Rectangle(targetCenter.X - radius, targetCenter.Y - radius, radius * , radius * );
 }

辅助方法 —— 计算眼球和眼珠的矩形位置

OK，完活，收工。

喜欢本系列丛书的朋友,可以点击链接加入QQ交流群(994761602)【C# 破境之道】
方便各位在有疑问的时候可以及时给我个反馈。同时，也算是给各位志同道合的朋友提供一个交流的平台。
需要源码的童鞋，也可以在群文件中获取最新源代码。