ACM北大暑期课培训第五天

　　今天讲的扫描线，树状数组，并查集还有前缀树。

　　

　　扫描线

  　扫描线的思路：使用一条垂直于X轴的直线，从左到右来扫描这个图形，明显，只有在碰到矩形的左边界或者右边界的时候，这个线段所扫描到的情况才会改变，所以把所有矩形的入边，出边按X值排序。然后根据X值从小到大去处理，就可以用线段树来维护扫描到的情况。

　　如果碰到矩形的入边，就把这条边加入，如果碰到出边，就拿走。

　　用根结点记录被覆盖的总长度     更新

　　插入数据的顺序：

　　　　 将矩形的纵边从左到右排序，然后依次将这些纵边插入线段树。要记住哪些纵边是一个 矩形的左边(开始边)，哪些纵边是一个矩形 的右边（结束边），以便插入时，对Len（当前,本区间上有多长的 部分是落在那些矩形中的）和 Covers（本区间当前被多少个矩形 完全包含）做不同的修改。 插入一条边后,就根据根节点的Len 值增加总 覆盖面积的值。 增量是Len * 本边到下一条边的距离。  一开始，所有区间 Len = 0 Covers = 0

　　扫描线和线段树推荐一个博客：https://www.cnblogs.com/AC-King/p/7789013.html

例题：POJ 1151 Atlantis

 #include <iostream>
 #include <algorithm>
 #include <math.h>
 #include <set>
 using namespace std;
 double y[];
 struct CNode
 {
     int L,R;
     CNode * pLeft, * pRight;
     double Len; //当前,本区间上有多长的部分是落在那些矩形中的
     int Covers;//本区间当前被多少个矩形完全包含
 };
 CNode Tree[];
 struct CLine
 {
     double x,y1,y2;
     bool bLeft; //是否是矩形的左边
 } lines[];
 int nNodeCount = ;
 bool operator< ( const CLine & l1,const CLine & l2)
 {
     return l1.x < l2.x;
 }
 template <class F,class T>
 F bin_search(F s, F e, T val)
 {
     //在区间[s,e)中查找 val,找不到就返回 e
     F L = s;
     F R = e-;
     while(L <= R )
     {
         F mid = L + (R-L)/;
         if( !( * mid < val || val < * mid ))
             return mid;
         else if(val < * mid)
             R = mid - ;
         else
             L = mid + ;
     }
     return e;
 }
 int Mid(CNode * pRoot)
 {
     return (pRoot->L + pRoot->R ) >>;
 }
 void Insert(CNode * pRoot,int L, int R)
 //在区间pRoot 插入矩形左边的一部分或全部，该左边的一部分或全部覆盖了区间[L,R]
 {
     if( pRoot->L == L && pRoot->R == R)
     {
         pRoot->Len = y[R+] - y[L];
         pRoot->Covers ++;
         return;
     }
     if( R <= Mid(pRoot))
         Insert(pRoot->pLeft,L,R);
     else if( L >= Mid(pRoot)+)
         Insert(pRoot->pRight,L,R);
     else
     {
         Insert(pRoot->pLeft,L,Mid(pRoot));
         Insert(pRoot->pRight,Mid(pRoot)+,R);
     }
     if( pRoot->Covers == ) //如果不为0，则说明本区间当前仍然被某个矩形完全包含，则不能更新 Len
         pRoot->Len = pRoot->pLeft ->Len + pRoot->pRight ->Len;
 }
 void Delete(CNode * pRoot,int L, int R)
 {
 //在区间pRoot 删除矩形右边的一部分或全部，该矩形右边的一部分或全部覆盖了区间[L,R]
     if( pRoot->L == L && pRoot->R == R)
     {
         pRoot->Covers --;
         if( pRoot->Covers ==  )
             if( pRoot->L == pRoot->R )
                 pRoot->Len = ;
             else
                 pRoot->Len = pRoot->pLeft ->Len + pRoot->pRight ->Len;
         return ;
     }
     if( R <= Mid(pRoot))
         Delete(pRoot->pLeft,L,R);
     else if( L >= Mid(pRoot)+)
         Delete(pRoot->pRight,L,R);
     else
     {
         Delete(pRoot->pLeft,L,Mid(pRoot));
         Delete(pRoot->pRight,Mid(pRoot)+,R);
     }
     if( pRoot->Covers == ) //如果不为0，则说明本区间当前仍然被某个矩形完全包含，则不能更新 Len
         pRoot->Len = pRoot->pLeft ->Len + pRoot->pRight ->Len;
 }
 void BuildTree( CNode * pRoot, int L,int R)
 {
     pRoot->L = L;
     pRoot->R = R;
     pRoot->Covers = ;
     pRoot->Len = ;
     if( L == R)
         return;
     nNodeCount ++;
     pRoot->pLeft = Tree + nNodeCount;
     nNodeCount ++;
     pRoot->pRight = Tree + nNodeCount;
     BuildTree( pRoot->pLeft,L,(L+R)/);
     BuildTree( pRoot->pRight,(L+R)/+,R);
 }
 int main()
 {
     int n;
     int i,j,k;
     double x1,y1,x2,y2;
     int yc,lc;
     int nCount = ;
     int t = ;
     while(true)
     {
         scanf("%d",&n);
         if( n == ) break;
         t ++;
         yc = lc = ;
         for( i = ; i < n; i ++ )
         {
             scanf("%lf%lf%lf%lf", &x1, &y1,&x2,&y2);
             y[yc++] = y1;
             y[yc++] = y2;
             lines[lc].x = x1;
             lines[lc].y1 = y1;
             lines[lc].y2 = y2;
             lines[lc].bLeft = true;
             lc ++;
             lines[lc].x = x2;
             lines[lc].y1 = y1;
             lines[lc].y2 = y2;
             lines[lc].bLeft = false;
             lc ++;
         }
         sort(y,y + yc);
         yc = unique(y,y+yc) - y;
         nNodeCount = ;
 //yc 是横线的条数，yc- 1是纵向区间的个数，这些区间从0
 //开始编号，那么最后一个区间
 //编号就是yc - 1 -1
         BuildTree(Tree, , yc -  - );
         sort(lines,lines + lc);
         double Area = ;
         for( i = ; i < lc -  ; i ++ )
         {
             int L = bin_search( y,y+yc,lines[i].y1) - y;
             int R = bin_search( y,y+yc,lines[i].y2) - y;
             if( lines[i].bLeft )
                 Insert(Tree,L,R-);
             else
                 Delete(Tree,L,R-);
             Area += Tree[].Len * (lines[i+].x - lines[i].x);
         }
         printf("Test case #%d\n",t);
         printf("Total explored area: %.2lf\n",Area);
         printf("\n",Area);
     }
     return ;
 }

老师上课讲的代码

　　树状数组

　　只能解决单点更新、区间求和问题。

　　可以快速求出任意区间和。

　　能力比线段树弱。  它能解决的问题线段树都能解决，是线段树能解决的问题的子集。

　　它的好处： 1.写起来简单    2.效率高（常数小）        ps:线段树常数大       两者区间查询的时间复杂度都是O(logn）

　　三个重要的函数 ：

int lowerbit(int x)
{
    return x&-x;
}

void Update(int i,int v)  // 初始化与单点修改
{
    while(i <= n)
    {
        c[i] += v ;
        i += lowbit(i) ;
    }
}

int Sum(int i)   // 区间求和
{
    int res =  ;
    while(i)
    {
        res += c[i] ;
        i -= lowbit(i) ;
    }
    return res ;
}

　　

　　lowbit(x)： 只保留x的二进制最右边的1，其余位都变为0后的值

　　对于序列a，我们设一个数组C   C[i] = a[i – 2 k + 1] + … + a[i]   C即为a的树状数组

　　k为i在二进制下末尾0的个数    2^k就是i 保留最右边的1，其余位全变0

　　 i从1开始算！

　　

　　C[i] = a[i-lowbit(i)+1] + …+ a[i] C包含哪些项看上去没有规律

　　C1=A1

　　C2=A1+A2

　　C3=A3

　　C4=A1+A2+A3+A4

　　C5=A5

　　C6=A5+A6

　　C7=A7

　　C8=A1+A2+A3+A4+A5+A6+A7+A8

　　 …………

　　C16=A1+A2+A3+A4+A5+A6+A7+A8+A9+A10+ A11+A12+A13+A14+A15+A16

　　树状数组图示

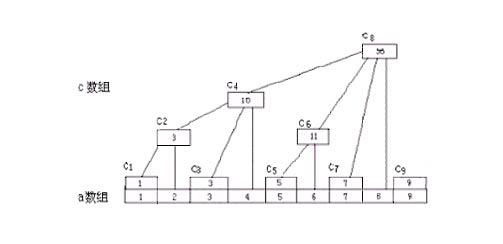
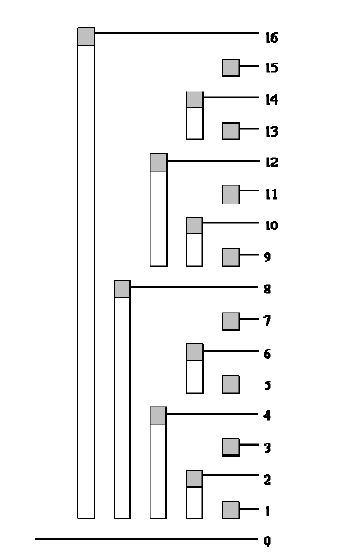
　　将C[]数组的结点序号转化为二进制

　　1=(001)      C[1]=A[1];

　　2=(010)      C[2]=A[1]+A[2];

　　3=(011)      C[3]=A[3];

　　4=(100)      C[4]=A[1]+A[2]+A[3]+A[4];

　　5=(101)      C[5]=A[5];

　　6=(110)      C[6]=A[5]+A[6];

　　7=(111)      C[7]=A[7];

　　8=(1000)    C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

　　对照式子可以发现  C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; （k为i的二进制中从最低位到高位连续零的长度）

　　时间复杂度：建数组： O(n) 更新： O(logn) 局部求和：O(logn)

　　树状数组推荐博客：https://www.cnblogs.com/ECJTUACM-873284962/p/6380245.html

　　POJ题目推荐： 2182, 2352, 1177, 3667,3067

　　并查集

　　3个操作：

　　1.合并两个集合

　　2.查询一个元素在哪个集合

　　3.查询两个元素是否属于同一集合

　　核心：查一个元素的树根（时间复杂度为常数）

　　实际应用代码：

 int par[];
 int GET_ROOT(int a)//查询一个元素在哪个集合  路径压缩
 {
     if (par[a]!=a)
         par[a] = GET_ROOT(par[a]);
     return par[a];
 }
 int query(int a,int b)//查询两个元素是否属于同一集合
 {
     return GET_ROOT(a)==GET_ROOT(b);
 }
 void merge(int a,int b)//合并两个集合
 {
     par[GET_ROOT(a)] = GET_ROOT(b);
 }

　　有时候需要添加数组记录，例如添加sum数组记录每个集合有多少元素。

　　在合并时进行维护

　　做题时主要理清怎样算同一集合。

例题：1.POJ 1611 The Suspects

　　　2.POJ 1988 Cube Stacking

　　　3.POJ 1182 食物链

　　DFA（一部分）

　   多模式匹配

　　trie图是一种DFA，可以由trie树为基础构造出来， 对于插入的每个模式串，其插入过程中使用的最后一 个节点都作为DFA的一个终止节点。 如果要求一个母串包含哪些模式串，以用母串作为 DFA的输入，在DFA 上行走，走到终止节点，就意 味着匹配了相应的模式串(没能走到终止节点，并不 意味着一定不包含模式串)。

　　避免母串指针回溯  -->  记住哪些模式串的哪个前缀已经被匹配  -->前缀指针

　　前缀指针：仿照KMP算法的Next数组， 我们也对树上的每一个节点 建立一个前缀指针。这个前 缀指针的定义和KMP算法中 的next数组相类似，从根节 点沿边到节点p我们可以得 到一个字符串S，节点p的前 缀指针定义为：指向树中出 现过的S的最长的后缀(不能等于S)。