第二十六篇 玩转数据结构——二分搜索树（Binary Search Tree）

 

 

 

1.. 二叉树

• 跟链表一样，二叉树也是一种动态数据结构，即，不需要在创建时指定大小。
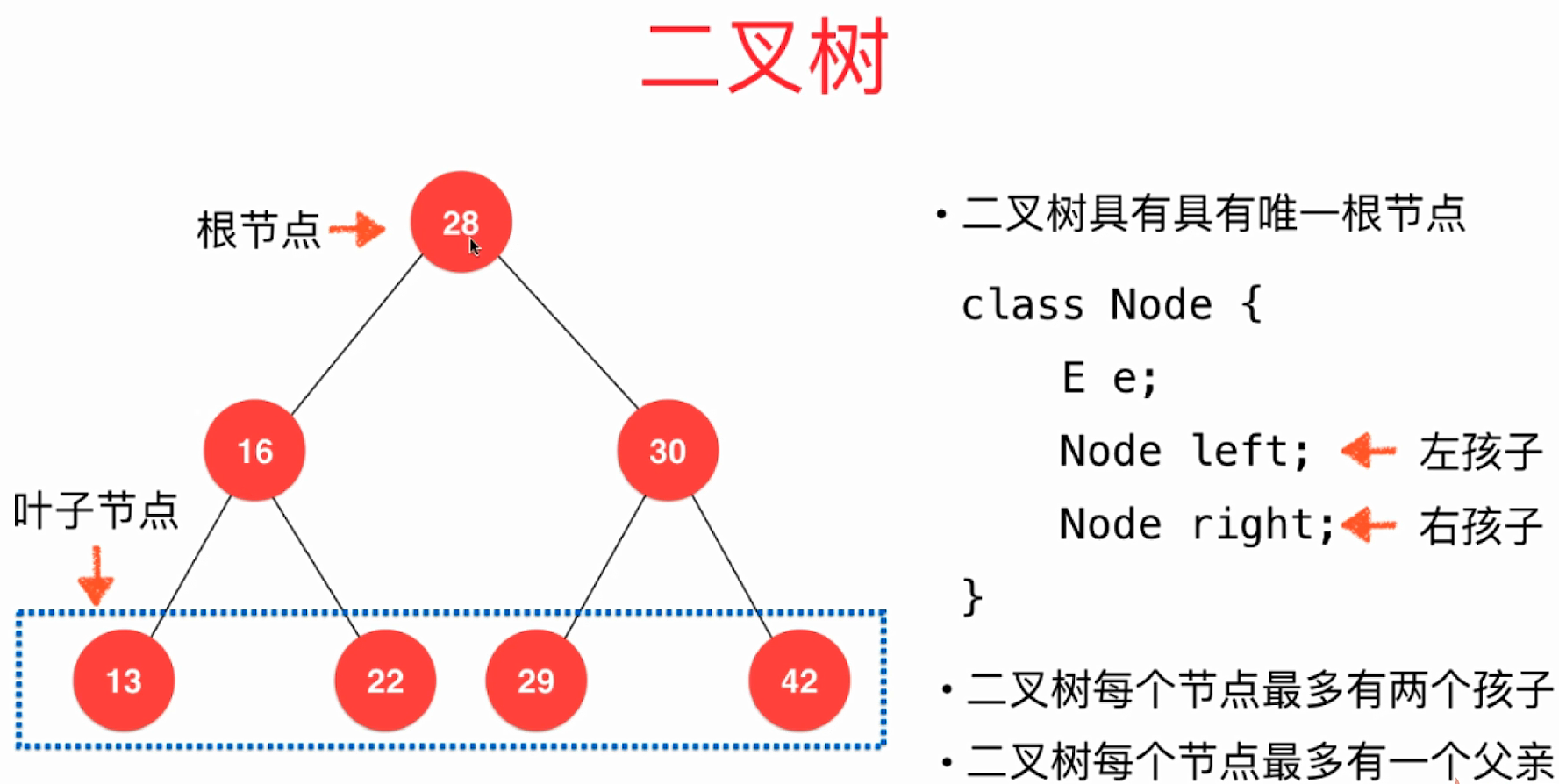
• 跟链表不同的是，二叉树中的每个节点，除了要存放元素e，它还有两个指向其它节点的引用，分别用Node left和Node right来表示。
• 类似的，如果每个节点中有3个指向其它节点的引用，就称其为"三叉树"...
• 二叉树具有唯一的根节点。
• 二叉树中每个节点最多指向其它的两个节点，我们称这两个节点为"左孩子"和"右孩子"，即每个节点最多有两个孩子。
• 一个孩子都没有的节点，称之为"叶子节点"。
• 二叉树的每个节点，最多只能有一个父亲节点，没有父亲节点的节点就是"根节点"。
• 二叉树的形象化描述如下图：
• 

• 二叉树具有天然的递归结构。
• 每个节点的"左子树"也是一棵二叉树，每个节点的"右子树"也是一棵二叉树。
• 二叉树不一定是"满的"，即，某些节点可能只有一个子节点；更极端一点，整棵二叉树可以仅有一个节点；在极端一点，整棵二叉树可以一个节点都没有；
• 

3.. 实现二分搜索树

• 二分搜索树的构造函数、getSize方法、isEmpty方法及add方法的实现逻辑如下：

• public class BST<E extends Comparable> {
  
      private class Node {
          public E e;
          public Node left, right;
  
          // 构造函数
          public Node(E e) {
              this.e = e;
              left = null;
              right = null;
          }
      }
  
      private Node root;
      private int size;  // 记录二分搜索树中存储的元素个数
  
      public BST() {
          root = null;
          size = 0;
      }
  
      // 实现size方法
      public int size() {
          return size;
      }
  
      // 实现isEmpty方法
      public boolean isEmpty() {
          return size == 0;
      }
  
      // 实现add方法
      public void add(E e) {
          root = add(root, e);
      }
  
      // 向以node为根的二分搜索树中插入元素e，递归算法
      // 返回插入新节点后二分搜索树的根
      private Node add(Node node, E e) {
  
          if (node == null) {
              size++;
              return new Node(e);
          }
  
          if (e.compareTo(node.e) < 0) {
              node.left = add(node.left, e);
          } else if (e.compareTo(node.e) > 0) {
              node.right = add(node.right, e);
          }
          return node;
      }
  }

• 二分搜索树的contains方法实现逻辑如下：

• // 实现contains方法，判断二分搜索树中是否包含元素e
  public boolean contains(E e) {
      return contains(root, e);
  }
  
  // 判断以node为根的二分搜索树中是否包含元素e
  private boolean contains(Node node, E e) {
      if (node == null) {
          return false;
      }
      if (e.compareTo(node.e) == 0) {
          return true;
      } else if (e.compareTo(node.e) < 0) {
          return contains(node.left, e);
      } else {
          return contains(node.right, e);
      }
  }

• 二分搜索树的遍历操作，遍历操作就是把所有节点都访问一遍
• 前序遍历的业务逻辑如下：

• //二分搜索树的前序遍历
  public void preOder() {
      preOrder(root);
  }
  
  private void preOrder(Node node) {
  
      if (node == null) {
          return;
      }
  
      System.out.print(node.e);
      preOrder(node.left);
      preOrder(node.right);
  }

• 中序遍历的业务逻辑如下：

• // 二分搜索树的中序遍历
  public void inOrder() {
      inOrder(root);
  }
  
  // 中序遍历以node为根的二分搜索树，递归算法
  private void inOrder(Node node) {
  
      if (node == null) {
          return;
      }
  
      inOrder(node.left);
      System.out.print(node.e);
      inOrder(node.right);
  
  }

• 后序遍历的业务逻辑如下：

• // 二分搜索树的后序遍历
  public void postOrder() {
      postOrder(root);
  }
  
  // 后序遍历以node为根的二分搜索树，递归算法
  private void postOrder(Node node) {
  
      if (node == null) {
          return;
      }
      postOrder(node.left);
      postOrder(node.right);
      System.out.print(node.e);
  
  }

• 简单测试如下：

• public class Main {
  
      public static void main(String[] args) {
          BST<Integer> bst = new BST<>();
          int[] nums = {5, 3, 6, 8, 4, 2};
          for (int num : nums) {
              // 测试add方法
              bst.add(num);
          }
          // 测试前序遍历
          bst.preOrder();
          System.out.println();
          // 测试中序遍历
          bst.inOrder();
          System.out.println();
          // 测试后序遍历
          bst.postOrder();
  
      }
  }

• 输出结果：

• 532468
  234568
  243865

• 前序遍历是最自然的遍历方式，也是最常用的遍历方式；中序遍历的结果是按从小到大的顺序的排列的；后序遍历可以用于为二分搜索树释放内存。
• 利用"栈"实现二分搜索树的非递归前序遍历

• // 二分搜索树的非递归前序遍历
  public void preOrderNR() {
      Stack<Node> stack = new Stack<>();
      stack.push(root);
      while (!stack.isEmpty()) {
          Node cur = stack.pop();
          System.out.print(cur.e);
          if (cur.right != null) {
              stack.push(cur.right);
          }
          if (cur.left != null) {
              stack.push(cur.left);
          }
      }
  }

• 二分搜索树的非递归实现比递归实现更加复杂。
• 二分搜索树的前序、中序和后续遍历都属于"深度优先"算法。
• 二分搜索树的"层序遍历"属于"广度优先"算法。
• 利用"队列"实现二分搜索树的"层序遍历"

• // 二分搜索树的层序遍历
  public void levelOrder() {
      Queue<Node> q = new LinkedList<>();
      q.add(root);
      while (!q.isEmpty()) {
          Node cur = q.remove();
          System.out.print(cur.e);
          if (cur.left != null) {
              q.add(cur.left);
          }
          if (cur.right != null) {
              q.add(cur.right);
          }
      }
  }

• 获取二分搜索树中的最小元素和最大元素

• // 寻找二分搜索树中的最小元素
  public E minimum() {
  
      if (size == 0) {
          throw new IllegalArgumentException("BST is empty.");
      }
      return minimum(root).e;
  
  }
  
  // 返回以node为根的二分搜索树的最小元素所在节点
  private Node minimum(Node node) {
      if (node.left == null) {
          return node;
      }
      return minimum(node.left);
  }
  
  // 寻找二分搜索树中的最大元素
  public E maximum() {
  
      if (size == 0) {
          throw new IllegalArgumentException("BST is empty.");
      }
      return maximum(root).e;
  
  }
  
  // 返回以node为根的二分搜索树的最大元素所在节点
  private Node maximum(Node node) {
      if (node.right == null) {
          return node;
      }
      return maximum(node.right);
  }

• 删除二分搜索树中最小元素和最大元素所在节点

• // 从二分搜索树中删除最小元素所在节点，返回最小元素
  public E removeMin() {
      E ret = minimum();
      root = removeMin(root);
      return ret;
  }
  
  // 删除掉以node为根的二分搜索树中的最小元素所在节点
  // 返回删除节点后新的二分搜索树的根
  private Node removeMin(Node node) {
      if (node.left == null) {
          Node rightNode = node.right;
          node.right = null;
          size--;
          return rightNode;
      }
      node.left = removeMin(node.left);
      return node;
  }
  
  // 从二分搜索树中删除最大元素所在节点，返回最小元素
  public E removeMax() {
      E ret = maximum();
      root = removeMax(root);
      return ret;
  }
  
  // 删除掉以node为根的二分搜索树中的最小元素所在节点
  // 返回删除节点后新的二分搜索树的根
  private Node removeMax(Node node) {
      if (node.right == null) {
          Node leftNode = node.left;
          node.left = null;
          size--;
          return leftNode;
      }
      node.right = removeMax(node.right);
      return node;
  }

• 删除二分搜索树中指定元素所对应的节点

• // 从二分搜索树中删除元素为e的节点
  public void remove(E e) {
      remove(root, e);
  }
  
  // 删除以node为根节点的二分搜索树中元素为e的节点，递归算法
  // 返回删除节点后新的二分搜索树的根
  private Node remove(Node node, E e) {
      if (node == null) {
          return null;
      }
  
      if (e.compareTo(node.e) < 0) {
          node.left = remove(node.left, e);
          return node;
      } else if (e.compareTo(node.e) > 0) {
          node.right = remove(node.right, e);
          return node;
      } else {
          // 待删除节点左子树为空的情况
          if (node.left == null) {
              Node rightNode = node.right;
              node.right = null;
              size--;
              return rightNode;
              // 待删除节点右子树为空的情况
          } else if (node.right == null) {
              Node leftNode = node.left;
              node.left = null;
              size--;
              return leftNode;
              // 待删除节点左右子树均不为空
              // 找到比待删除节点大的最小节点，即待删除节点右子树的最小节点
              // 用这个节点顶替待删除节点
          } else {
              Node successor = minimum(node.right);
              successor.right = removeMin(node.right);  //这里进行了size--操作
              successor.left = node.left;
              node.left = null;
              node.right = null;
              return successor;
          }
      }
  }