6_14 Abbott的复仇（UVa816）<图的最短路BFS>

1999次世界总决赛的比赛包括一个骰子迷宫问题。在这个问题被写的时候，法官们无法发现骰子迷宫概念的原始来源。不久之后的比赛，但是，罗伯特先生雅培，无数的迷宫和对作者的创造者主题，联系大赛评委，自称是骰子迷宫的鼻祖。很遗憾，我们没有信用艾伯特他原来的概念在去年的问题陈述。但是我们很高兴地报告，Abbott先生提供了自己的专业知识，这一年他的原创大赛未穿过箭头迷宫。
例如大多数的迷宫，走过迷宫是被箭从交叉路口直到达到目标路口。由于每个路口从一个给定的方向接近，靠近路口的一个标志指示在哪个方向的交叉点可以退出。
这些方向总是左，向前或向右，或任何组合这些。
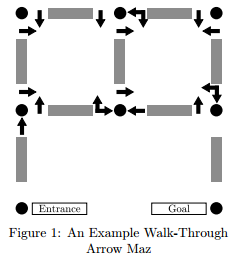
图1显示了一个通过箭头迷宫行走。交叉口是出（行，列）对，以左上为（1,1）。图1入口路口（3,1），和目标相交（3,3）。你开始迷宫由向北从（3,1）。当你走在（3,1）为（2,1），标志在（2,1）表明，当你接近（2,1）从南（向北行驶）你可以继续走了。继续前进会带你走向（1,1）。标志在（1,1）作为你的方法从南表明你可以退出（1,1）只有通过正确。这让你到东方步行从（1,1）向（1,2）。到目前为止还没有做出选择。同样的情况，当你继续从（1,2）到（2,2）到（2,3）到（1,3）。现在，然而，当你移动向西方（1,3）（1,2），你必须继续直或左转弯的选择。继续直将带你走向（1,1），向左，你会南（2,2）。实际的（独特的）这个迷宫求解下列顺序交叉：（3,1）（2,1）（1,1）（1,2）（2,2）（2,3）（1,3）（1,2）（1,1）（2,1）（2,2）（1,2）（1,3）（2,3）（3,3）。
你必须写一个程序来通过箭头走迷宫的有效解决。解一个迷宫就意味着（如果可能的话）找到一条穿过规定方向的迷宫的路径，并在目标中结束。这条路线不应该比必要的时间长，当然。

【输入】

输入文件将包含一个或多个箭头的迷宫。每个迷宫的描述的第一行包含迷宫的名字，这是不超过20个字符的字母数字字符串。下一行包含，在以下顺序中，起始行、起始列、起始方向、目标行，最后的目标列。所有被一个空格分隔。这个问题的最大尺寸为9，为9，因此所有行和列数字为9至1的单位数。
起始方向为北、南、东、西三个字符的字符之一，分别为。
迷宫的所有剩余的输入线都有这样的格式：2个整数，一个或多个字符组，和哨兵的星号，又都用一个空格分隔。整数代表行和列，一个迷宫的交叉路口。每个字符组表示该路口的一个标志。小组中的第一个字符是“氮”，“电子”或“瓦特”，以指示在什么方向的旅行的标志将被看到。例如，“”表示，这是在南部旅行时所看到的标志。（这是第一个方向的字符是一对三个箭头字符。这些可以是'升'，'福'或'的指示左，向前，和权利，分别。
在第一列中包含一个单一的零的行的列表的交点。下一行的输入开始下一个迷宫等。输入端是一行的“结束”这个词本身。

【输出】

对于每一个迷宫，输出文件应该包含一行名称的迷宫，然后由一个或多个线与一个解决方案的迷宫或短语'没有可能的解决方案。迷宫的名字应该在1列开始，和所有其他线路应在3列，即开始，缩进两个空格。解决方案应输出为一个列表的格式的交叉点（的），他们被访问的目标，应该由一个单一的空间分隔，所有的解决方案的最后一行应该包含10个交叉点。

注：

罗伯特秘密穿过箭头迷宫实际上是用于大规模的建设，而不是纸。虽然他的迷宫是未发表的，他们中的一些人实际上已建成。其中一个是在亚特兰大博物馆展出。其他人已经在过去两年的暑假里建造了美国迷宫公司。正如它们的名字所表明的这些迷宫都要走过。
为爱冒险，2图形罗伯特伦敦的亚特兰大的迷宫图。
即使你对整个迷宫有一个概要的解决，解决这个问题也是相当困难的。想象一下，如果你在迷宫中穿行，只看到了一个问题。
一个符号在一个时间！罗伯特雅培自己表明，迷宫太复杂，大多数人放弃之前整理。
没有放弃的人是唐纳德：他花了三十分钟解决迷宫。
图1：通过箭头MAZ以下示例中输入第一个迷宫图1例走迷宫。

Sample Input
SAMPLE
3 1 N 3 3
1 1 WL NR *
1 2 WLF NR ER *
1 3 NL ER *
2 1 SL WR NF *
2 2 SL WF ELF *
2 3 SFR EL *
0
NOSOLUTION
3 1 N 3 2
1 1 WL NR *
1 2 NL ER *
2 1 SL WR NFR *
2 2 SR EL *
0
END

Sample Output
SAMPLE
(3,1) (2,1) (1,1) (1,2) (2,2) (2,3) (1,3) (1,2) (1,1) (2,1)
(2,2) (1,2) (1,3) (2,3) (3,3)
NOSOLUTION
No Solution Possible