SIFT算法原理（2）-极值点的精确定位

在SIFT解析（一）建立高斯金字塔中，我们得到了高斯差分金字塔；

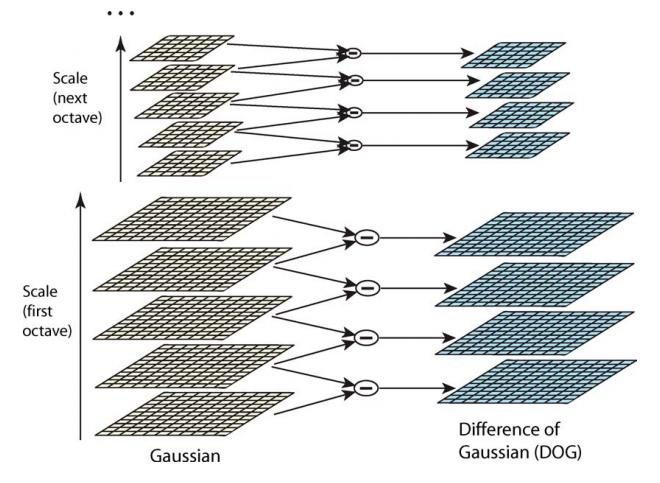
检测DOG尺度空间极值点

SIFT关键点是由DOG空间的局部极值点组成的.以中心点进行3X3X3的相邻点比较,检测其是否是图像域和尺度域的相邻点的极大值或极小值.

（1）为了确保不是噪声我们先进型阈值二值化；

n和S一样，你想提取多少个图片的特征；（n）S表示每组提取多少层

（2）在差分金字塔中找极值点

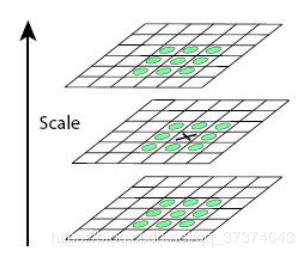
特征点是由DOG空间的局部极值点组成的。为了寻找DoG函数的极值点，每一个像素点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小。特征点是由DOG空间的局部极值点组成的。如上图，中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。

由于像素是离散的，且尺度空间也是离散的（前后尺度成k倍），有可能找到的极值点是真正极值点旁边的点，如下图：

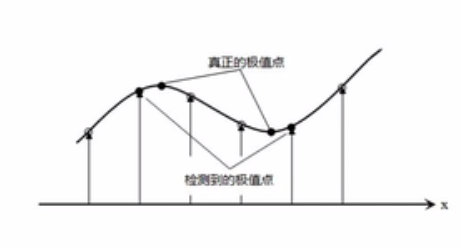
因此需要极值点的精确定位； 利用已知的离散空间点插值得到的连续空间极值点的方法叫做子像素插值（Sub-pixel Interpolation）。

（3）极值点的精确定位

为了提高关键点的稳定性，需要对尺度空间DoG函数进行曲线拟合。利用DoG函数在尺度空间的Taylor展开式(拟合函数)为：

求导方法：就是利用相邻像素差值代替求导

可参考：sift算法原理详解(三)

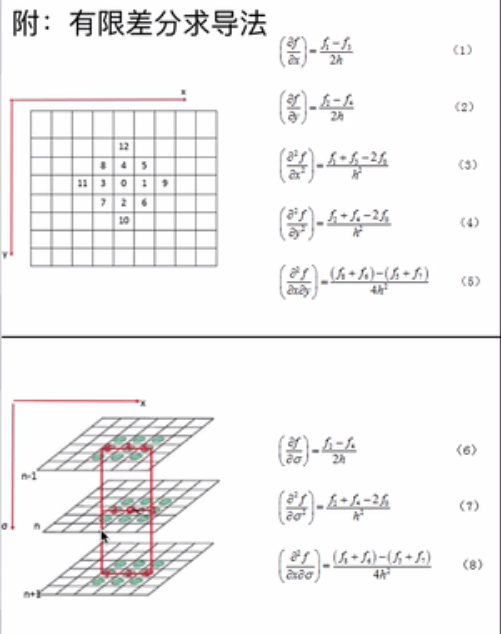
检测到的极值点对应极值点的方程为：

（4）舍去低对比度的极值点

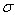其中,代表相对插值中心的偏移量，当它在任一维度上的偏移量大于0.5时（即x或y或），意味着插值中心已经偏移到它的邻近点上，所以必须改变当前关键点的位置。同时在新的位置上反复插值直到收敛；也有可能超出所设定的迭代次数或者超出图像边界的范围，此时这样的点应该删除，在Lowe中进行了5次迭代。另外，过小的点易受噪声的干扰而变得不稳定，所以将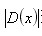小于某个经验值(Lowe论文中使用0.03，Rob Hess等人实现时使用0.04/S)的极值点删除。同时，在此过程中获取特征点的精确位置(原位置加上拟合的偏移量)以及尺度()。

对应公式：T取0.04，n和S一样，你想提取多少个图片的特征；（n）S表示每组提取多少层

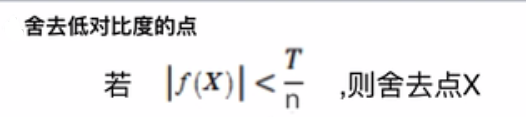
(5)边缘效应的去除（Hessian矩阵）

具体的海森矩阵数学公式可以参考：https://blog.csdn.net/qq_33854260/article/details/69808970 和  https://blog.csdn.net/qq_39521554/article/details/78895869

其与图像的关系：https://blog.csdn.net/lwzkiller/article/details/55050275

H（x,y）就是高斯差分金字塔中对x,y的二阶导数，及

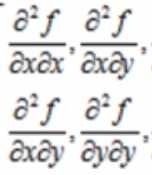
然后我们需要知道矩阵的迹（Tr(H)）是矩阵的特征根之和（α和β）和行列式的计算(Det(H））；

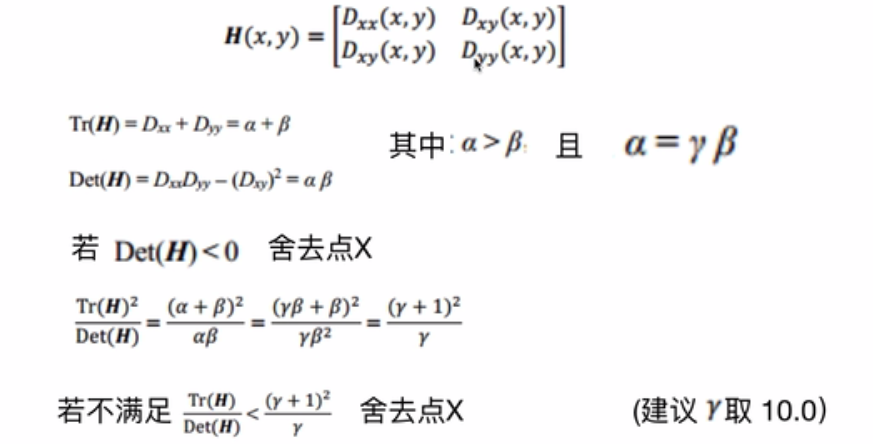
首先我们知道在OpenCV——Harris、Shi Tomas、自定义、亚像素角点检测

harris焦点检测中的特征值的变化可以检测出边缘；

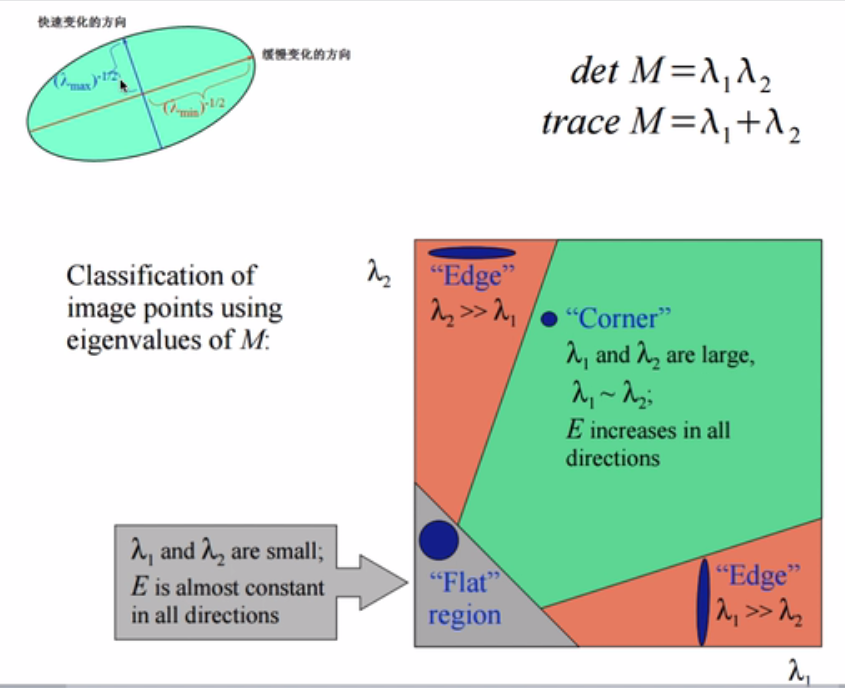
同理，既然我们能检测出边缘，就可以剔除边缘点；及希望特征根α和β两个值相差不多，及没有边缘效应；故希望r小于一定的阈值；

令为α最大特征值，β为最小的特征值，则公式的值在两个特征值相等时最小，随着的增大而增大。值越大，说明两个特征值的比值越大，即在某一个方向的梯度值越大，而在另一个方向的梯度值越小，而边缘恰恰就是这种情况。所以为了剔除边缘响应点，需要让该比值小于一定的阈值，因此，为了检测主曲率是否在某域值r下，只需检测

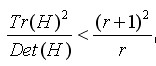(4-7)

式(4-7)成立时将关键点保留，反之剔除。

原文链接：https://blog.csdn.net/qq_37374643/article/details/88606351

参考：SIFT算法原理详解